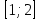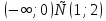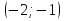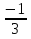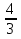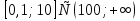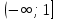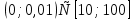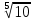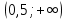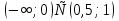Разработка урока по математике в 10 классе по теме «Решение логарифмических и показательных уравнений и неравенств»
 Скачать 46.33 Kb. Скачать 46.33 Kb.
|
| Методическая разработка урока по математике в 10 классе по теме « Решение логарифмических и показательных уравнений и неравенств». учителя математики Ляшенко Н.Н. Цели урока: обобщение и систематизация знаний учащихся по теме «Показательная и логарифмическая функции»; закрепление умений и навыков решения показательных и логарифмических уравнений и неравенств; совершенствовать математическую речь. Ход урока. 1.Орг. момент. Сообщение темы урока. Постановка целей урока. 2.Актуализация учебного процесса. 1).Теоретический опрос (фронтально). а). Определение показательной функции, её свойства и график. б). Применение свойств показательной функции при решении неравенств. в). Определение логарифма. г). Свойства логарифмов. д).Определение логарифмической функции, её свойства и график. е). Применение свойств логарифмической функции при решении неравенств. ( Для корректировки ответов учащихся на экране высвечиваются правильные ответы; рисунки графиков). 2). Математический диктант. 1вариант. а). Записать ООФ показательной. б). Записать формулу: логарифм произведения. в). Записать формулу перехода к новому основанию. г). Решить:  . .д). Решить: 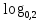 y y 7. 7.2вариант. а). Записать ООФ логарифмической. б). Записать формулу: логарифм частного. в). Записать основное логарифмическое тождество. г). Решить: 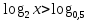 5. 5.д). Решить:  . .На экране предлагаются ответы, поэтому учащиеся выполняют самопроверку и самооценку своей работы. 3.Закрепление умений и навыков учащихся. К доске вызываются 4 сильных учащихся. Решаем из учебника А.Н.Колмагорова 2 уравнения и 2 неравенства, остальные учащиеся, эти упражнения выполняют по 1 на 4 варианта. № 188 (а), № 188 (в), № 202(а), № 203 (а) Каждый проверяет своё решение и решение одноклассника на доске. Исправляем ошибки, если они есть. 4. Самостоятельная работа. Класс разделён на 4 группы. Даются задания каждой группе. Задание 1 группе. В 1614 году были опубликованы первые логарифм. таблицы, составленные Джоном … . Они помогли астрономам и инженерам, сокращая время на вычисления. Решите примеры и узнаете его имя. 1).  +3=0; Н +3=0; Н2).  (2 (2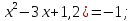 E E3).  -5⋅ -5⋅ +6=0; О +6=0; О4). ( 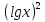  3lgx+2=0; А 3lgx+2=0; А5). 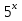 +2⋅ +2⋅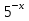 -3=0; Б -3=0; Б6).  -3⋅ -3⋅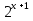 +8≤0; П +8≤0; П7). 1÷( 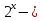 1)+ 1)+ 3; В⋅ 3; В⋅8). 2  (lgx (lgx lg0,1) lg0,1) 1÷(lgx) 1÷(lgx) 0. Р 0. РЗадание 2 группе. Ещё недавно трудно было представить инженера без логарифмической линейки в кармане, изобретённая через десяток лет после появления логарифмов Непера английским математиком, имя которого вы узнаете, решив свои задания. 1). 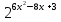 -5⋅ -5⋅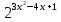 +2=0; Р +2=0; Р2). 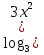 -5x+1)=1; Е -5x+1)=1; Е3).  2⋅ 2⋅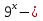 3=0; Т 3=0; Т4). 2 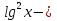 lgx lgx 7=0; О 7=0; О5). 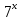 +2⋅ +2⋅ =0; К =0; К6).   4⋅ 4⋅ +27 +27 0; Н 0; Н7). 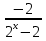 + +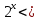 3; У 3; У8). 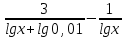 ≤0. Г ≤0. ГЗадание 3 группе. Первые попытки распространить логарифмы на комплексные числа предприняли на рубеже 17-18 веков Лейбниц и Бернулли. Полная теория логарифмов отрицательных и комплексных чисел была опубликована …?…. В 1747-1751г.г. и по существу не отличается от современной. Найти имя учёного. 1).  + + 3=0; Й 3=0; Й2). 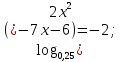 А А3). 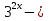 8⋅ 8⋅ 9=0; Л 9=0; Л4). 3 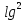 x x 5lgx+2=0; О 5lgx+2=0; О5). 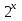 + +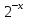 -2=0; Е -2=0; Е6). 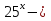 4⋅ 4⋅ 5≤0; Р 5≤0; Р7). 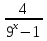 + + 5; Ф 5; Ф8). lgx+ 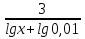 ≥ ≥ 2. Э 2. Э Задание 4 группе. В России первые таблицы логарифмов были изданы в 1703г. при участии русского учёного, имя которого вы мне назовёте, решив свои задания. 1). 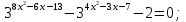 А А2). 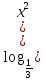 17x+9)=-3; Н 17x+9)=-3; Н3).  +16=0; Г +16=0; Г4). 5 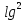 x+4lgx x+4lgx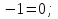 Ц Ц5). 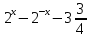 =0; К =0; К6).  И И7). 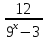 +7 +7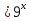 ; Й ; Й8). lgx+  ≤5. М ≤5. МТаблицы с ответами для групп: 1 группа:
2 группа:
3 группа:
4 группа:
4. Итоги урока. Оценки учащимся. 5. Д/з. Повторить теоретический материал. |