|
«Решение задач с помощью систем уравнений»
«Где есть желание, найдется путь».
План-конспект открытого урока по алгебре в 7 а классе
Учитель высшей квалификационной категории Краснова Лидия Егоровна
Школа – ГБОУ ЦО № 1462
Дата проведения : 19 апреля 2013 года.
Количество учащихся – 23.
Тема урока : «Решение задач с помощью систем уравнений».
Урок представляет практикум по решению задач, составляя систему уравнений и выражение одной переменной через другую.
Определение места урока в изучаемой теме, разделе, курсе:
Урок является вторым в разделе решение задач с помощью систем уравнений.
Универсальные учебные действия:
Личностные – осознание учащимися важности составления систем для решения задач, умение оценивать себя.
Познавательные – умение извлекать нужную информацию из прочитанного текста.
Коммуникативные- через стихи, диалоги ( умение слушать и излагать свое мнение).
Регулятивные – взаимный контроль( исправление ошибок у соседа по парте), самоконтроль ( умение понимать причины ошибок), контроль со стороны учителя.
Цели урока: развитие познавательного интереса при решении задач,
создание учебно-методических условий, способствующих достижению обучающимися следующих результатов:
- предметных:
осмысление ранее изученных понятий «выражение переменных из формул» и «способы решения систем уравнений различными способами», умения составлять уравнения по тексту задачи в разнообразных интерпретациях; применять правила выражения переменных; овладения навыкам составления и решения уравнений , систем для решения несложных задач.
- метапредметных:
1) творческого решения практических задач; умения самостоятельно выполнять творческую работу;
2) способность вступать в речевое общение, участие в диалоге;
3) формировать умения оценивать свои учебные достижения, своё эмоциональное состояние.
- личностных:
1) проявление воли и настойчивости для достижения конечных результатов;
2) умение выдвигать гипотезы, отыскивать доказательства и рассуждать логично;
3) выработка уверенности во взаимоотношениях с людьми;
4) умения уверенно и легко выполнять математические операции.
5) формировать навыки самостоятельной работы и самооценки знаний.
Задачи урока:
образовательная: способствовать совершенствованию полученных знаний по применению и развитию при работе с задачами,
практическая: обучение навыкам поискового чтения из текста с извлечением информации для составления уравнения,
развивающая: проверить уровень самостоятельной деятельности обучающихся по применению знаний в различных ситуациях,
воспитательная: способствовать развитию любознательности и творческой активности обучающихся.
Описание применяемых образовательных технологии, обоснование их использования:
Здоровьесберегающие технологии ( физкультминутка, минута психологической разгрузки, правильная осанка при записи, освещение класса).
Игровые ( стихи, старинные задачи) – чтобы вызвать интерес и активность учащихся и способствовать более быстрому и прочному запоминанию алгоритма составления уравнений.
Формы и методы работы на уроке подобраны исходя из психолого-педагогических особенностей данного класса.
Используются формы работы: а)индивидуальная, б)групповая, в)фронтальная.
Оснащение урока:
Учебно-методические пособия: учебник «Алгебра 7».
Разработки уроков по алгебре для 7 класса по учебнику под редакцией Теляковского.
Раздаточный материал, подготовленный учителем для решения.
Используемые технологии: а)уровневой дифференциации, б)индивидуального обучения, в)проблемно поисковой, г) групповые.
Методы работы:
1) методы организации учебно-познавательной деятельности: а)словесный, б)наглядный, в)практический, г)самостоятельная работа, д) работа под руководством.
2) методы контроля и самоконтроля: а)устный опрос, б)фронтальный опрос, в)письменный контроль, г)тест, д) взаимный контроль, е) самоконтроль
Планируемый результат:
Знать:
способы решения систем линейных уравнений,
алгоритм решения задач,
Уметь:
применять удобный способ решения систем линейных уравнений,
применять алгоритм решения задач на практике,
использовать различные источники знаний,
работать с карточками различного содержания,
работать в группах, индивидуально.
План урока.
1. Организационный момент.
2. Актуализация знаний.
3 Физкультминутка.
4. Минута психологической разгрузки.
5. Решение задачи.
6. Рефлексия.
7. Самооценка.
8. Подведение итогов урока.
9. Домашнее задание.
Ход урока.
Деятельность учителя
|
Деятельность ученика
|
Мы сегодня закрепим способы решения систем уравнений и составление систем уравнений к задачам. Открыли тетради, записали число, классная работа, тему урока.
– Вы все к сегодняшнему уроку готовились решать задачи, выполняли практические задания. Оцените свои знания по данной теме и в течение всего урока проверите насколько ваша оценка соответствует действительности: кто-то может, завысил, кто-то занизил, так-что старайтесь.
Мы сегодня на уроке будем решать задачи, определяя свой рациональный путь. Удачи!
|
Приветствие.
Запись в тетрадях числа, классной работы и темы урока.
|
Деятельность учителя II 1,2,3; III 3); V а),б)
|
Деятельность ученика
I, 4); VII д)
|
Вчера один из учеников решал с ошибкой и никак не мог выразить одну переменную через другую. Давайте поможем.
|
Весь класс решает тест (проверка с помощью доски и обмен тетрадями с соседом по парте)
Выразить х через у х+3у=6
1)х=6-3у,
2)х=-6-3у,
3) х=6+3у
Выразить у через х 2х-у=3
1) у= 3-2х,
2) у =-3 +2х,
3) у=3+2х.
Решением системы уравнений 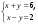 является пара является пара
1) (-4;-2)
2) (4; 2),
3) (-4; 2)
Результат сложения уравнений х+5у =7, 3х-2у=4 равен
1) 4х-3у =11,
2) 4х+7у 11,
3) 4х+3у =11
Графики прямых параллельны, то система имеет решение:
1) единственное,
2) много решений,
3) не имеет решений
|
3. Физкультминутка.
Деятельность учителя IV 1);
|
Деятельность ученика
|
Учитель монотонным голосом предлагает отдохнуть учащимся.
Закройте глаза.
Расслабьтесь. Поводите глазами вверх, вниз, влево, вправо.
Откройте глаза.
Потянитесь как маленькие котята.
Улыбнитесь друг другу.
И с хорошим настроением продолжим работу.
|
Учащиеся выполняют все указания учителя молча.
|
4.Минута психологической разгрузки
Деятельность учителя III 4);
|
Деятельность ученика II 1); VII д);
|
В развитии алгебры как науки большую роль сыграла книга английского физика и математика Исаака Ньютона «Всеобщая арифметика» изданная в 1707 году. В предисловии к своей книге он писал, что алгебраическим путем решаются очень трудные задачи, решение которых было бы тщетно искать при помощи одной арифметики»
В своей «Всеобщей арифметике» Ньютон называет буквы, знаки действий, алгебраические выражения и уравнения языком алгебры. Ньютон оказал огромное влияние на последующее развитие алгебры. После него авторы учебников уже рассматривали алгебру как общую арифметическую дисциплину, математику -занимающуюся изучением и дальнейшим развитием численных методов решения алгебраических уравнений.
|
Один из учеников подготовил сообщение и рассказывает всем учащимся.
В истории арифметики и алгебры большое значение имеют труды Мухаммеда Ал-Хорезми. Он написал книгу, посвященную решению уравнений, которая называлась «Книга о восстановлении и противопоставлении». Книга начинается с введения чисел, далее идет представление главной темы первого раздела книги- решения уравнений. Все представленные уравнения являются линейными или квадратными и состоят из чисел, их квадратов и корней. Интересно отметить, что во всех книгах Аль-Хорезми, математические вычисления фиксируются исключительно при помощи слов, ни один символ, таким образом, им не использовался. Преобразование выполняется посредством двух операций - ал-джабр и ал- мукабала. Слово « ал-джабр» Ал-Хорезми употребляется в значении «восполнение» для обозначения процесса перенесения слагаемых из одной части уравнения в другую термин « ал-мукалаба» означает « противопоставление» и используется для обозначения процесса сокращения равных членов в обеих частях уравнения. От слова «ал-джабр» возникло слово « алгебра»
|
5.Решение задач.
Деятельность учителя I 3); II 2); III 1),2),3); VI в); VII в
|
Вы должны были прочитать задачи с помощью составления систем уравнений. В каких случаях при решении задачи целесообразно составлять не уравнение, а систему? [когда есть две величины, которые не связаны напрямую] Естественно, почти во всех случаях, когда можно составить уравнение, можно составить и систему, и наоборот.
Поэтому, что именно составлять, надо решать в каждом конкретном случае. Не бойтесь вводить «лишние» переменные – это упрощает составление системы, а эти переменные уничтожатся сами!
«Предмет математики настолько серьёзен, что полезно, не упуская случая, сделать его немного занимательным»
Задача № 1115 из учебника
Как-то лошадь и мул вместе вышли из дома,
Их хозяин поклажей большой нагрузил,
Долго-долго тащились дорогой знакомой,
из последней уже выбивался сил.
«Тяжело мне идти» - лошадь громко стонала.
Мул с иронией молвил (нес он тоже немало)
«Неужели, скажи, я похож на осла?
Может, я и осел, но вполне понимаю:
Моя ноша значительно больше твоей.
Вот представь: я мешок у тебя забираю,
И мой груз стал в два раза, чем твой, тяжелей.
А вот если тебе мой мешок перебросить,
Одинаковый груз наши спины б согнул»
Сколько ж было мешков у страдалицы-лошади?
Сколько нес на спине умный маленький мул?
|
Деятельность ученика IV 2); VI в)
|
Учащиеся заполняют таблицу
две неизвестные величины
|
было
|
когда мул забрал мешок стало
|
когда мул отдал мешок стало
|
поклажа, которую несла лошадь
|
х
|
х-1
|
х+1
|
поклажа, которую нес мул
|
у
|
у+1
|
у-1
|
1 уравнение
|
2(х-1)=у+1
|
2 уравнение
|
х+1=у-1
|
№ 1105 из учебника самостоятельно
|
|
Рефлексия (концентрация внимания).
Деятельность учителя II 4); V в)
|
Деятельность ученика I 2); VII б;
|
Учитель читает задание, написанное на доске.
Решить системы уравнений
|
Поднятая правая рука ученика выражает мысль о желании ответить.
1) 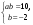 ; 2) ; 2) 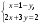 ; 3) ; 3) 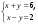 . .
|
Самооценка
Деятельность учителя II 5);
VII 2 е)
|
Деятельность ученика I 4);
|
Учитель предлагает оценить свою работу на уроке учащимся и поставить оценки
|
|
вид работы
|
оценка
|
1
|
сделал тест
|
|
2
|
правильно оформил и решил задачу № 1115
|
|
3
|
заполнил таблицу к задаче №1105
|
|
4
|
составил систему уравнений
|
|
5
|
решил устно систему уравнений
|
|
6
|
активно работал на уроке
|
|
|
Подведение итогов урока
Деятельность учителя II 2)
|
Деятельность ученика VI в)
|
На каких уроках вы уже встречались со словом система уравнений?
«Всякая хорошо решенная математическая задача доставляет умственное наслаждение» Г.Гессе
Вы активно поработали на уроке, приятно было с вами работать. Что сегодня на уроке вам понравилось?
|
Физика – Международная система единиц. Биология – система кровообращения человека. Химия – периодическая система элементов Д.И.Менделеева Русский язык – система частей речи, система гласных. Учащиеся делятся впечатлениями от урока
|
Домашнее задание.
Придумать или найти необычную задачу, которая решается с помощью системы уравнений, решить её и оформить все на альбомном листе. |
|
|
 Скачать 107.18 Kb.
Скачать 107.18 Kb.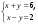 является пара
является пара 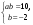 ; 2)
; 2) 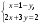 ; 3)
; 3)