Решение квадратных уравнений с применений теоремы Виета
 Скачать 50.58 Kb.
|
   Открытый урок по алгебре в 8 классе на тему:«Решение квадратных уравнений с применений теоремы Виета». Тип урока: урок повторения и обобщения изученного материала. Учитель высшей категории МОУ «СОШ №55» г. Саратова Петрова Людмила Дмитриевна Образовательные цели урока. Обеспечить закрепление теоремы Виета. Обратить внимание учащихся на решение квадратных уравнений  , в которых 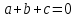 или  ; привить навыке устного решения таких уравнений.Воспитательные цели урока. Способствовать выработке у школьников умения обобщать изучаемые факты; развивать самостоятельность путём составления или уравнений. Формирование общеучебных умения. Главный труд детей – это учёба, прочное овладение знаниями. Те умения и навыки, с помощью которых реализуются учебные задачи, называются учебными умениями и навыками. Среди них выделяются такие, которые присущи учебной работе при обучении любому школьному предмету, например, умение работать с учебным текстом, умение составлять план предстоящей работы, умение проверить полученный результат. Такие навыки и умения называют общеучебными. Ход урока
а) 1) x2+x-2=0 (x=-2; x=1) 2) x2+2x-3=0 (x=-3; x=1) 3) x2-3x+2=0 (x=2; x=1) б) 1) x2-x-2=0 (x=-1; x=2) 2) x2-2x-3=0 (x=-1; x=2) 3) x2-3x-4=0 ( x=-1; x=4) в) 1) x2+7x+12=0 (x=-4; x=-3) 2) 5x2+11x+2=0 (x=-2; x=- 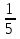 )3) x2-8x+15=0 (x=13; x=5) Итак, мы на протяжении нескольких уроков решали квадратные уравнения. Дайте определение квадратного уравнения. Какие виды квадратных уравнений вы знаете? (приведенные, неполные) От чего зависит, имеет ли квадратное уравнение корни? Запишите формулы для решения квадратных уравнений.
Решите уравнение и выполните проверку по теореме, обратно теореме Виета. X2-2x-2=0 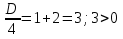 X1,2=1±3 Проверка. x1 + x2 =2 = -b x1 x2 = -2 = c
Определите знаки корней уравнения, не решая его. х2-18х+17=0 D=324-68=256. D>0, 2 различных действительных корня. х1х2=17, следовательно, х1 и х2 одного знака. х1+х2=18, следовательно, х1 и х2 – положительные корни.
Х2+2х-63=0 D=256-252=4; 4>0. х1х2=-63, следовательно, корни разных знаков. х1+х2=-2, следовательно, модуль отрицательного корня больше, чем модуль положительного. х=-9 или х=7. Проверка по теореме, обратной теореме Виета. Пока учащиеся готовятся к ответу, с классом проверить правильность решения уравнений из д/з. Выяснить способы решения квадратных уравнений. Как выяснить, верно ли решено квадратное уравнение?
Каковы ещё возможные применения теоремы Виета и теоремы, обратной ей? (Ответы учеников 2,3)
Уравнения из д/з. 1а) х2+х-2=0 а=1; в=1; с=-2. а+в+с=0 2а) х2+2х-3=0 а=1; в=2; с=-3. а+в+с=0 3а) х2-3х+2=0 1-3+2=0 Чему равна сумма коэффициентов в этих уравнениях? (Нулю) Какое число является корнем каждого из них? (х=1) Вывод (записать) Если в уравнении ах2+bх+с=0 сумма коэффициентов а+b+c=0, то один из корней уравнения равен 1, а другой, в соответствии с теоремой Виета, равен 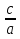 или g.Верно и обратное: Если один из корней квадратного уравнения равен 1, то второй корень равен 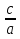или a+b+c=0.Упражнение №534.
3-7+4=0 Х1=1 Х2=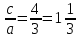 
5-8+3=0 Х1=1 Х2=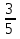 
5-6+1=0 у1=1 у2=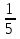
х2-х-2=0 х2-2х-3=0 х2-3х-4=0 1-(-1)-2=0 1-(-2)-3=0 1-(-3)-4=0 ах2+bx+с=0 a-b+c=0 х=-1 или х= - 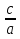Упражнение №539. г) х2-22-23=0 1-(-22)-23=0 х=-1 х=23 е) 15х2-22х-37=0 15+22-37=0 х1=-1 х2=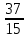 
1 вариант
(1;-18)
(-1;  )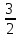
(-1;40)
(1; 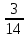 )2 вариант
(1;  )
Если квадратное уравнение с целыми коэффициентами имеет хотя бы один корень, то он является делителем свободного члена. Решить уравнение: 3х2+7х+2=0 D>0, 2 различных действительных корня. х1+х2= -  оба корня отрицательны х1х2 = 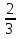 Если уравнение имеет хотя бы один целый корень, то это может либо -1, либо -2. Но -1 не является корнем, т.к. 3-7+2≠0. Проверим х=-2: 34-14+2=0. Да. Тогда х1=-2; х2= -  .
На протяжении последних трёх уроков мы наблюдали чудесные возможности теоремы Виета. Поистине можно сказать: «Это разноликая теорема Виета!». Мне бы хотелось повторить её формулировку в несколько необычной форме: По праву достойна в стихах быть воспета О свойствах корней теорема Виета. Что лучше, скажи, постоянства такого: Умножишь ты корни – и дробь уж готова? В числителе с, в знаменателе а. А сумма корней тоже сумме равна. Хоть с минусом дробь, что за беда, В числителе b, в знаменателе а. Слово ученику (из истории о Ф. Виете)
Используя возможности теоремы Виета, решить уравнения: № 541 (б,в) 586 (а) 587. |
)
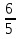