«Развивающие задачи в процессе обучения математике»

Название	«Развивающие задачи в процессе обучения математике»
Дата	11.03.2016
Размер	271.87 Kb.
Тип	Документы

«Эффективные механизмы поддержки учеников с повышенной познавательной активностью. Использование развивающих заданий на уроках математики и во внеурочное время, как важнейшее направление работы с одаренными детьми»

из опыта работы учителя математики

МБОУ СОШ№32 г. Энгельс Саратовской обл.

Татьяны Владимировны Логиновой.

2015г

План.

1.Эффективные механизмы поддержки учеников с повышенной познавательной активностью.

2. Ознакомление с теоретическим и дидактическим материалами по теме «Развивающие задачи в процессе обучения математике»

3. Разбор решения задач развивающего характера для учащихся 5-11 классов

4. Предоставление материалов из собственного опыта работы учителя по использованию задач с развивающими функциями на уроках математики в 5-11 классах или во внеурочное время.

Многие думают, что ребенок, опережающий сверстников по уровню интеллекта, блещущий умственными способностями, не будет встречать трудностей в учебных занятиях – ему, очевидно, уготовано более счастливое, чем у других детство. В действительности же детей с ранним умственным расцветом могут ожидать немалые сложности и дома, и в школе. Поэтому необходимо диагностировать и выявлять одаренных детей не только потому, что они являются творческим и умственным потенциалом своей страны, но и для того, чтобы устранить дискомфорт, который может возникнуть в общении с обыкновенными детьми. Для этого необходимо: разрабатывать для одаренных детей индивидуальные планы, создавать для детей с повышенными способностями особые классы в структуре массовой общеобразовательной школы, создавать лицеи и гимназии для одаренных

Большинству учителей просто некогда заниматься одаренными детьми, а некоторым из них как бы мешают ученики с познаниями, с не всегда понятной умственной активностью. Бывает и так: педагог поначалу собирается давать явно выдающемуся ученику более трудные задания, уделять ему специальное внимание. Но потом такие намерения, а иногда и обещания родителям, забываются – нет для этого у учителя ни времени, ни сил. К тому же в ученике незаурядном, с необычно высоким умственным уровнем педагог нередко видит, прежде всего, лишь восприимчивого к учению, не замечая, что такой ребенок нуждается в особом подходе.
Трудности могут начаться с того, что ребенок, опережающий сверстников, склонен постоянно привлекать к себе внимание. Стремительное выполнение заданий, готовность правильно ответить на вопрос учителя – для него желанная умственная игра, состязание. И он торопливее других тянет руку – радостный, предвкушая одобрение. И при этом все время жаждет новой умственной пищи. Но это через какое-то время надоедает и учителю, и другим ученикам, и ему самому. Такой ученик постоянно становится всем в классе в тягость.
Часто в школе наиболее развитого ученика почти перестают спрашивать: учитель ведь уверен, что он и так знает. Если он все же настойчиво пытается что-нибудь сказать или спросить, то может нарваться на упрек, что он «выскочка». А когда он видит, что его активность учителю не нужна, то переключается на что-нибудь постороннее – не миновать недовольства, а то и раздражения педагога: почему отвлекается и не интересуется занятиями? Уж не слишком ли он о себе возомнил?
Так поначалу энтузиаст учебных занятий, ребенок становится лишним в школе, а она ему – ненужной. Он предпочитает болеть, лишь бы не посещать уроки. В результате уже в первые же школьные годы и тем более подростковые многие выдающиеся дети оказываются в конфликте с учителями. А те иногда и сами не знают, чем такой ребенок их раздражает: с одной стороны все-таки вундеркинд, а с другой – «какой-то ненормальный». Причина такого конфликта в том, что наиболее способные ученики нуждаются в нагрузке, которая была бы под стать их умственным силам; а наша средняя школа, кроме средней программы, ничем им помочь не может.
Бывают и другие варианты школьных трудностей у ребенка с ранним умственным расцветом. От него ожидают, требуют и родители, и педагоги, чтобы он обязательно был примерным учеником, отличником. А ведь отметки часто ставят не только за знания, но и за поведение, за почерк. Ученику с повышенными способностями достается гораздо больше, чем другим, например, за невыполненное домашнее задание, за какое-нибудь не предусмотренное темой высказывание на уроке, небрежную домашнюю работу. А в некоторых семьях любое снижение отметок воспринимается как драма.
У ребенка с ранним умственным расцветом нередки трудности и во взаимоотношениях со сверстниками. Часто одноклассники, особенно к началу подросткового возраста, начинают активно отторгать от себя такого ученика, делают ему обидные прозвища, стараются поставить его в неловкое положение. Чтобы не оказаться отверженным, стремиться быть «как все»: избегать обнаруживать себя самым знающим или тем более самым старательным.
Человеческое мышление, способность к творчеству – величайший дар природы. Очень важно отметить, что даром этим природа отмечает каждого человека. Но очевидна и мысль о том, что свои дары природа поровну не делит и кого-то награждает больше, а кого-то меньше. Одаренным же принято называть того, чей дар явно превосходит некие средние возможности, способности большинства.
Важно этот дар в ребенке разглядеть, помочь ему, поддержать его. Такому ребенку особенно необходима помощь взрослых: родителей, воспитателей, социальных педагогов, учителей. В школе одаренному ребенку нужна педагогическая поддержка со стороны учителя.
Суть педагогической поддержки заключается в содействии ученику в его начинаниях, первых робких, неуверенных действиях: педагог их позитивно оценивает, одобряет, если надо, встает на сторону ученика, формирует положительное общественное мнение, защищает его права и т.д. Сущность педагогической поддержки может быть понята и шире как создание безопасной среды, благоприятного эмоционального фона, развивающей среды.
Эта категория детей требует к себе особого индивидуального социально-педагогического подхода. Поэтому, для более успешного восстановления социального статуса одаренных детей как личности, члена коллектива (сверстников, одноклассников, ближайшего социального окружения) специалисту (социальному педагогу, педагогу-психологу, учителю) необходимо в работе соблюдать рад социально-педагогических условий.
Одаренных детей, как правило, отличают:
• высокая любознательность;
• исследовательская активность;
• повышенная биохимическая активность мозга;
• эмоциональность;
• вспыльчивость;
• особая речь, моторика и восприятие.
Важно такого ребенка вовремя заметить и помочь ему.
В процессе воспитания и обучения детей надо не игнорировать появляющееся у них качественное своеобразие способностей и одаренности, а развивать его, применяя различные методы. О.д. нуждаются в особом воспитании, специальных, индивидуальных учебных программах, специально подготовленных учителях, специальных школах.
Одаренному ребенку нужна педагогическая поддержка.
Цель педагогической поддержки – максимально содействовать школьнику в осознании и реализации потребности в самореализации.
Основные направления поддержки одаренных детей:
1. Вселение в них уверенности в их способности жить в обществе, найти в нем свое место, сформировать адекватную Я-концепцию;
2. Выработка у одаренных детей умения правильно себя оценивать и ставить реальные цели;
3. Преодоление психологической изоляции одаренных детей в ученических коллективах.
Социально-педагогическая поддержка предполагает объединение усилий общества и педагога. Какие установки и методы можно предложит педагогам:

Огромную роль здесь играют развивающие задачи в системе обучения математике

Если в недавнем прошлом основной задачей, стоящей перед учителем, была передача ученикам определенной суммы знаний, то в настоящее время на первый план выдвигается задача развития личности в процессе обучения.

Так, в рамках реализации ФГОС обучение математике в современной школе направлено на достижение таких целей, как:

-формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

-воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

-формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

-развитие представлений о математике как форме описания и методе познания действительности;

-формирование общих способов интеллектуальной деятельности, являющихся основой познавательной культуры.

Отметим, что согласно современной Концепции математического образования,

утвержденной Распоряжением Правительства РФ от 24.12.2013 No2506-р, важнейшей целью школьного образования является интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для полноценной жизни в обществе. Для достижения поставленных целей целесообразно использовать систему развивающих задач, которая направлена на достижение обучающимися креативности мышления, инициативы, находчивости, активности при решении математических задач, что отражает личностное направление их развития. Использование развивающих задач в процессе обучения способствует активизации самостоятельной познавательной деятельности школьников, является важнейшим средством формирования у школьников системы основных математических знаний, умений и навыков, ведущей формой учебной деятельности, средством их математического развития. От эффективности применения развивающих задач в обучении математике во многом зависит и степень готовности школьников к последующей за обучением практической деятельности в любой сфере производства и культуры.

Математика – метод и язык познания окружающего мира. Исходя из этого вывода, учителю необходимо понимать, что математике нужно научить каждого ученика, различие может быть только в объеме изучаемого материала. Но очень важно создание условий для выявления, развития и реализации способностей одаренных и высокомотивированных детей.

Для этого, исходя из интересов и особенностей познавательной деятельности учащихся, учитель должен помогать учащимся за деталями увидеть сущность понятия, приемы или методы решения (доказательства), их структуру; раскрывать взаимосвязь между родственными понятиями, их свойствами и признаками; нацеливать школьников на их самостоятельное выделение, показывая при этом необходимость и пользу такой проработки; тщательно вскрывать взаимосвязь между прямыми и обратными действиями, взаимно обратными понятиями, учить использовать эту взаимосвязь как для самопроверки, так и для уменьшения нагрузки на память.

Необходимо вырабатывать у учащихся умение определять главное в рассуждении, избегать многословности, но при этом кратко и логически грамотно пояснять каждый этап в доказательстве теоремы и решении задачи.

Очень важно ставить перед учащимися задания, требующие самостоятельного их поиска или создания, подбирать задачи, содержательная сторона которых соответствует реальной действительности. По возможности использовать для них материал, отвечающий интересам учеников, имеющий положительную эмоциональную окраску. При этом надо учить их при решении задачи переходить на абстрагированный уровень, отвлекаясь от конкретного содержания.
Основные направления моей работы с одаренными детьми:

- Создание проблемных ситуаций;

- организация самостоятельной, творческой деятельности учащихся на уроке;

- работа с различными источниками информации: учебниками, книгами, справочниками, энциклопедиями, словарями;

- побуждение учеников к оценке деятельности других учащихся, самооценке и самокоррекции, поощрение выражения их собственной точки зрения;

-связь изучаемого материала с повседневной жизнью и интересами учащихся, характерными для их возраста;

-оценивание достижений учащихся не только отметкой-баллом, но и характеристикой результата.

-создание ситуации успеха на уроке, поддержание школьников, столкнувшихся с учебными проблемами - позволяют сформировать у обучающихся ключевые компетентности.
В целях поддержки интереса к предмету и развития природных задатков учащихся я использую творческие задания, занимательные материалы и задачи. Использую развивающие задачи, которые предлагаю учащимся в качестве разминки в начале урока. На решение таких задач я отвожу не более 1 минуты и требую обязательно подробного объяснения хода решения задачи. В случае затруднения даю подсказки, подробно разбираем эти задачи.
Например:

ЦЕПОЧКА ВЫЧИСЛЕНИЙ	ОТВЕТЫ
1) Вычислить, записать ответ.
2) Увеличить полученное число на
3) Результат записать в виде неправильной дроби
4) Умножить на число, обратное полученному
5) Найти 25% от результата
6) Разделить на
7) Полученный результат – это 10% от некоторого числа Найти это число

Проверяем ответы стоя. Если ученик ошибся, то он садится.

Существуют разные классификации развивающих заданий .

1. Введение вспомогательной неизвестной.

Введение вспомогательной неизвестной – это эвристический приём, используемый в алгебре для формоизменения текста задачи. В 5-м классе можно использовать вид этого приёма – это использование различного рода обозначения чисел или числовых выражений с целью упрощения процесса вычислений.

Тема: «Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями», пример: 96 ·

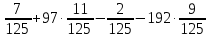.Решение. Пусть

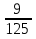= a,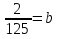

,тогда 96 (a-b)+97 (a+b)-b-192a=a

Ответ.

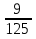
Такие примеры хороши для дифференцированной работы на уроке, сильные – отыскивают путь решения, остальные – в очередной раз отрабатывают распределительный закон и упрощение выражений.

2.Приём получения следствий.

Приём получения следствий состоит в том, что раскрытие содержания исходных данных задачи даёт возможность получить некоторые выводы, а из полученных результатов сделать новые выводы и т.д. Нередко, таким образом, удаётся найти решение задачи.

Тема: «Умножение натуральных чисел».

Пример 1. Сколько всего прабабушек и прадедушек было у всех ваших прапрабабушек и прапрадедушек?

Решение. У каждого человека было 8 прапрабабушек и 8 прапрадедушек, всего 16 человек. У каждого из этих 16-ти тоже было по 16 прямых предков в «четвёртом колене», следовательно, искомое число 16 ·16=256

Тема: «Деление натуральных чисел».

Пример 2. Делимое в 6 раз больше делителя, а делитель в 6 раз больше частного. Чему равно делимое, делитель и частное.

Решение. Делимое в 6 раз больше делителя, следовательно, частное равно 6. Если частное равно 6, а делитель в 6 раз больше частного, следовательно, делитель равен 36 и, следовательно, делимое равно 36·6=216. Ответ: делимое 216, делитель 36, частное 6.

3.Перебор.

Сущность данного приёма заключается в проведении перебора всех возможных случаев, описанных в задаче, что особенно ценно, в групповом анализе возможных решений.

В курсе 5-го класса можно решать огромное количество задач на перебор. Начинаем, как всегда, с простейших.

Пример 1. В двузначном числе в два раза больше единиц, чем десятков. Если к этому числу прибавить 36, то получится число, записанное теми же цифрами. Найдите это число.

Решение. Перебираем двузначные числа, удовлетворяющие условию12; 24; 36; 48. Прибавляем к каждому 36 и выбираем 12+36=48, 24+36=60, 36+36=72,48+36=84 искомое число. Ответ: 48.

Постепенно, при решении задач такого плана, формируется определённый навык. И можно уже брать задания, где уже надо показать единственность решения.

Пример 2. На складе имеются гвозди в ящиках по 16 кг, 17 кг, 40 кг. Может ли кладовщик отпустить 100кг гвоздей, не вскрывая ящики?

Решение. 1). Если один ящик по 40 кг, то оставшиеся 60 нельзя получить из 16 и 17.

2). Аналогично, если взять 2 ящика по 40 кг. Следовательно, кладовщик может брать только ящики по 16 кг и 17 кг.

3). Один 16 кг, то 84 кг нельзя составить из ящиков по 17 кг.

4). Два по16 кг, то 16 ·2=32,68:17=4

Итак, 100 кг = 2·16кг+4·17кг.

Покажем, что задача имеет единственное решение:3·16=48, 4·16=64, 5·16=80, 6·16=96.

Только по 17 нельзя, т.к. 100 не делится на 17.

Замечание. Второй путь. Рассмотреть 1, 2, 3, 4, 5 ящиков по 17 кг и подсчитать, можно ли оставшийся вес в каждом случае составить из ящиков по 16 кг.

Хорошо с помощью перебора отрабатывать: геометрический материал; задачи на движение, в которых не указано направление движения; порядок действий, в заданиях, где надо расставить всеми возможными способами скобки и т.д.

4.Сравнение

Сравнение – процесс количественного или качественного сопоставления разных свойств (сходств, отличий, преимуществ и недостатков) двух объектов.

К заданиям на сравнение относятся: задания на обнаружение сходных признаков, отличных признаков, на полное сравнение.

Примеры:

1. Чем похожи числа?

а) 7 и 71

б) 33 и 4444

в) 31 и 38

г) 400, 114, 488 и 242

В данных заданиях несколько объектов в значительной степени сходны друг с другом и только один отличается от остальных. Главное требование – выявление лишнего объекта.

Тема: «Геометрические фигуры».

Пример. Исключите лишнюю фигуру.

5Аналогия.

Аналогия – это мыслительная операция, с помощью которой находится сходство между объектами в некотором отношении. Использование аналогии в математике является одной из основ поиска решения задач.

Примеры:

1. Уменьшаемое – разность, множитель - ….?

2. Продолжите ряд: а) 1, 5, 13, 29,…. б) 1, 4, 9, 16,….

в) 7, 19, 37, 61,… г) 1, 8, 27….

3. Найдите пропущенное число

5х-2=3	3х-4=2	9х+8=35	6х-3=21
1	8	27	?

Найдите неизвестное число

15-х=11	34	Х+5=8
3х-2=1	?	13-х=11

Найдите неизвестное число

МЕТРО	МЕТР	8-Х=3
ОКРУГ	КРУГ	4х+7=11
РОМБ	РОМ	5+7х=?

6.Логические задачи

Логические задачи не имеют прямой связи с каким-либо учебным материалом. Их можно использовать с целью воспитания умения проводить доказательные рассуждения. Сюда относятся задачи на взвешивания, переливания, разрезания.

Пример 1. В мешке 24 кг гвоздей. Как, имея только чашечные весы без гирь, отмерить 9 кг гвоздей?

Пример 2. Из девяти монет одна фальшивая, она легче остальных. Как за два взвешивания на чашечных весах без гирь определить, какая именно монета фальшивая?

Решение. 1) Взять по три монеты. Если весы в равновесии, то фальшивая в тройке не на весах, если равновесия нет, то фальшивая в лёгкой тройке. 2) Взять по одной монете, если весы в равновесии, то фальшивая не на весах, если равновесия нет, то фальшивая легче.

Пример 3. Как из восьмилитрового ведра, наполненного молоком, отлить 1л с помощью трёхлитровой банки и пятилитрового бидона?

Решение.

Ведро 8л	8	3	3	6	1
Бидон 5л	0	5	2	2	5
Банка 3л	0	0	3	0	2

При систематическом использовании задач на описанные выше приёмы на уроках, в домашних заданиях и дополнительных занятиях можно помочь школьникам приобрести необходимый опыт и выработать собственную систему эвристических приёмов, позволяющих творчески подходить к решению незнакомых задач.

Для удобства в планировании такой работы учителю хорошо иметь систематизированную по темам школьного курса математики и приёмам эвристики подборку задач. Ниже приведены такие задачи: 5-6 классы

	1. В одной коробке лежат два белых шара, в другой — два черных, в третьей — один белый и один черный. На каждой коробке имеется рисунок, но он неправильно указывает содержимое коробки. Из какой коробки, не глядя, надо вынуть шар, чтобы можно было определить содержимое каждой коробки?
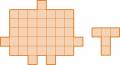	2. Разрежьте фигуру на буквы "Т".
	3. Размеры бандероли 10 см × 4 см × 3 см. Её можно перевязать тремя разными способами. В каком случае длина верёвки будет наименьшая?
	4. В примере на сложение различные фигурки заменяют различные цифры. Какую цифру заменяет квадратик?

7-8 классы

		1. В классе 15 человек говорят по-английски, 20 - по-итальянски, 8 - по-немецки, 3 - по-немецки и по-английски, 5 - по-немецки и по-итальянски, 6 - по-итальянски и по-английски. Сколько человек в классе, если всеми тремя языками владеет 1 человек?
		2. Какое слово зашифровано: 222122111121? Каждая буква заменена своим номером в русском алфавите.
		3. Каждый из треугольников и квадрат имеют периметр 16 см. Чему равен периметр нарисованного восьмиугольника?
	4. Листок календаря частично закрыт предыдущим оторванным листком. Вершины A и B верхнего листка лежат на сторонах нижнего листка. Четвёртая вершина нижнего листка не видна — она закрыта верхним листком. Верхний и нижний листки, естественно, равны между собой. Какая часть нижнего листка больше — закрытая или открытая?

5. Чему равны произведения
(1 − 1/4)(1 − 1/9)(1 − 1/16) ... (1 − 1/225);
(100 − 1²) (100 − 2²) (100 − 3²) ... (100 − 25)?

9-11 классы

	1. На каком из рисунков закрашена большая площадь? (Сторона каждого квадрата делится на 3 равные части.)
	2. Четыре одинаковые игральные кости уложены так, как показано на рисунке. Сколько точек на самой нижней грани?
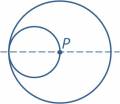	3. Окружность радиуса 1 катится без скольжения по окружности радиуса 2 с внутренней стороны. На меньшей окружности отмечена точка Р, которая в начальном положении совпадает с центром большей окружности. Какова траектория точки Р?
	4. Каково отношение площади закрашенной части к площади белой части?

7.Задания, направленные на развитие внимания

Внимание – направленность и сосредоточенность психической деятельности на определенном объекте или действии.

Внимание бывает двух видов: непроизвольное (непреднамеренное) внимание – возникает без усилий, само по себе, и произвольное (преднамеренное) внимание – предполагает постановку цели, и приложение усилий и стараний для сосредоточения. Развитию и укреплению произвольного внимания способствуют:

1) осознание человеком значения задачи – чем важнее задача, чем сильнее желание выполнить ее, тем в большей мере привлекается внимание;

2) интерес к конечному результату деятельности заставляет напоминать себе, что надо быть внимательным;

3) постановка вопросов по ходу выполнения задания, ответы на которые требуют внимания помогают сосредоточиться;

4) словесный отчет, что уже сделано и что еще надо сделать и т. д.

В учебный материал можно включить содержательно-логические задания, направленные на развитие различных характеристик внимания: его объема, устойчивости, умения переключать внимание с одного предмета на другой, распределять его на различные предметы и виды деятельности.

Упражнение 1

Посмотрите на незнакомую картинку в течение 3-4 сек.

Перечислите детали (предметы), которые запомнились.

Ключ:

запомнили менее 5 деталей — плохо;
запомнили от 5 до 9 деталей — хорошо;
запомнили более 9 деталей — отлично.

Упражнение 2

Назовите количество групп из трех последовательных цифр, которые в сумме дают 15:

489561348526419569724

Упражнение 3

Сколько цифр одновременно делятся на 3 и на 2:

33; 74; 56; 66; 18

Упражнение 4

1. Поставьте будильник перед телевизором во время какой-либо интересной программы.

2. В течение 2-х минут удерживайте внимание только на секундной стрелке, не отвлекаясь на ТВ-передачу.

Упражнение 5

1. Возьмите два фломастера.

2. Попробуйте рисовать одновременно обеими руками. Причем одновременно начиная и заканчивая. Одной рукой — круг, второй — треугольник. Круг должен быть по возможности с ровной окружностью, а треугольник — с острыми кончиками углов.

3. Теперь попробуйте нарисовать за 1 мин. максимум кругов и треугольников.

4. Система оценивания:

меньше 5 — плохо;
5-7 —средне;
8-10 — хорошо;
больше 10 — отлично.

Упражнение 6

Отыщите во фразах спрятанные имена (пример: «Принесите кофе дяде» — Федя).

1. Невкусный этот омар и яблоки тоже. Няня, дай свежие — в апельсиновом желе!

2. Не мешает и майский свет, а плохо мне от ночи ранней.

3. Принеси горький перец с летнего рынка, пожалуйста!

4. Ковал я железо ярким днем.

8.Задания, направленные на развитие восприятия и воображения

Восприятие – это основной познавательный процесс чувственного отражения действительности, ее предметов и явлений при их непосредственном действии на органы чувств. Оно является основой мышления и практической деятельности как взрослого человека, так и ребенка, основой ориентации человека в окружающем мире, в обществе. Психологические исследования показали, что одним из эффективных методов организации восприятия и воспитания наблюдательности является сравнение. Восприятие при этом становится более глубоким. В результате игровой и учебной деятельности восприятие само переходит в самостоятельную деятельность, в наблюдение.

Обучение восприятию и умению наблюдать через упражнения на развитие восприятия, на восприятие формы, на развитие глазомера и решением задач с не сформулированным вопросом, с недостающими данными, с лишними данными, с взаимопроникающими элементами, нереальных задач.

Для развития воображения на уроках математики используются задания на составление фигур, построение фигуры из заданных фигур; упражнения на формирование способности понимать математические термины, взаимное расположение фигур, распознавание и выделение определенных геометрических фигур из общего числа фигур, деление заданной геометрической фигуры, составление фигуры из фиксированного числа частей, преобразование и перестраивание геометрических фигур, отыскание и пересчет предметов, представленных в завуалированном виде, восстановление фигур или предметов и простейшие задания по топологии.

https://shkolapifagora.my1.ru/0995/096/1-17.jpg

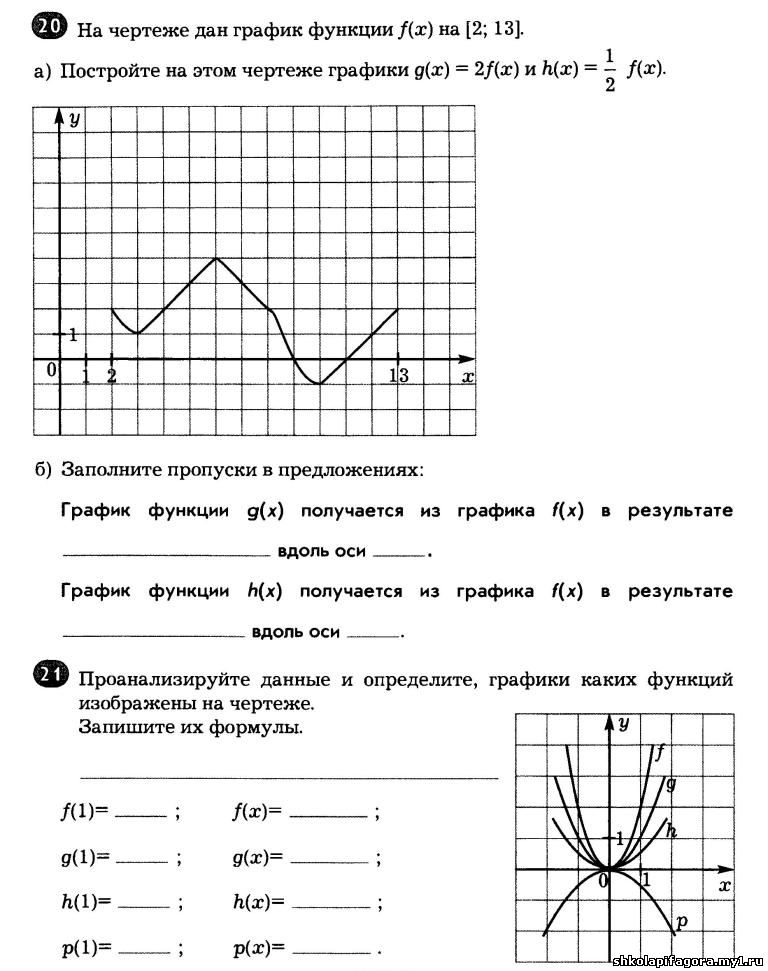
https://shkolapifagora.my1.ru/0995/096/1-4.jpg

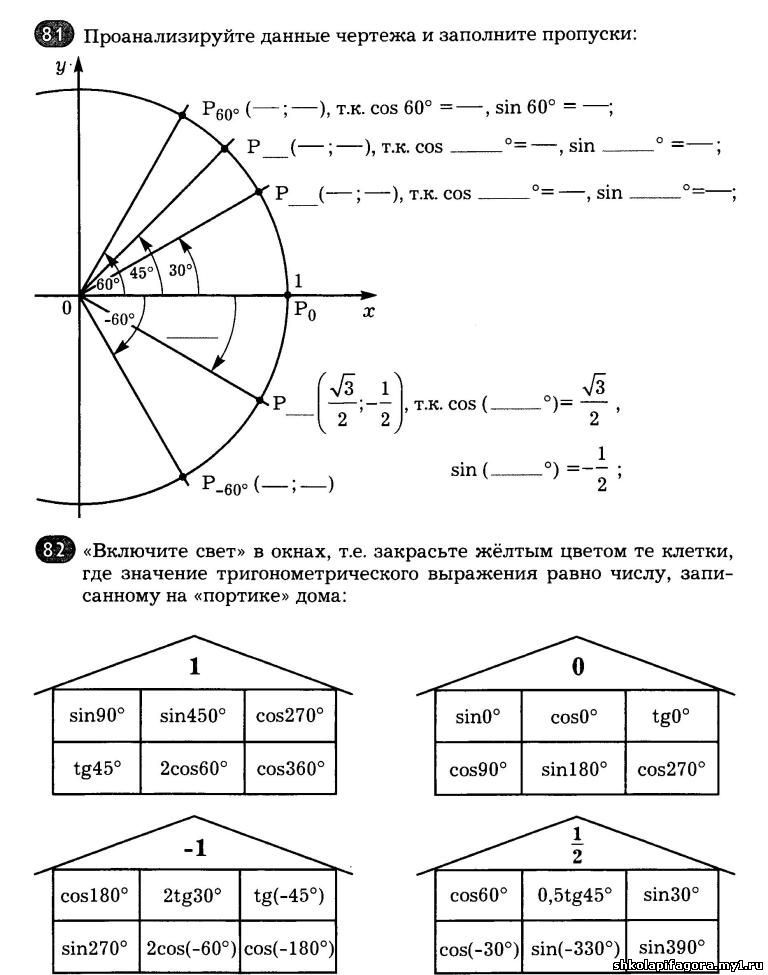
https://shkolapifagora.my1.ru/kirill/01/80.jpg

9.Задания, направленные на развитие памяти

Память является одним из основных свойств личности. Древние греки считали богиню памяти Мнемозину матерью девяти муз, покровительниц всех известных наук и искусств. Человек, лишенный памяти, по сути дела перестает быть человеком. Память – это одно из необходимых условий для развития интеллектуальных способностей. У младших школьников более развита память наглядно образная, чем смысловая. Уже в среднем звене школы необходимо развивать логическую память. Учащимся приходится запоминать определения, доказательства, объяснения. Приучая детей к запоминанию логически связанных значений, мы способствуем развитию их мышления.

Для развития математической памяти, используются, в частности, приемы мысленного составления плана, соотнесения, реконструкции, использования стимулирующих звеньев, выделения смысловых опорных. Для развития памяти представляют определенный интерес задачи с лишними данными, нереальные задачи, задачи с несколькими решениями и упражнения типа математические слова, цепочка слов, повтори-ка, зрительный диктант.

Например:1.Задания со сменой установки.

-На доске записано несколько чисел: 10,3,

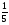, 100, 18. Я вам предлагаю их запомнить в том же порядке. Теперь я убираю этот ряд чисел, а вы должны постараться ответить на мои вопросы, вспоминая то, что было написано. Вопросы:

1) Сколько было чисел, которые делятся на 5 без остатка? (2)

2) Каким по счету было число, соответствующее порядковому номеру месяца октября в году? (первым)

3) В словесной записи скольких чисел есть буква «т»? ( во всех)

4) Порядковый номер какого дня недели получится при делении последнего числа на второе? (субботы)

5) Сколько было нечетных чисел? (1)

6) Какой месяц соответствует второму числу? (март)

7) В какую букву надо вписать число 17, чтобы получилось последнее число? (в О)

8) Какая цифра записана в разряде десятков четвертого числа? (0)

9) Какой будет правильная дробь, составленная из первого и второго числа? (

)

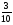10) Какой будет правильная дробь, составленная из четвертого и последнего числа? (

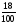
11) Что общего между дробям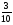и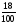

? (знаменатели обеих дробей- единица с нулями)

12) Результат деления второго числа на первое? (

)

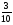Юра после прогулки рассказал: «У озера видел жука, трёх гусей, двух уток, жаворонка и четырёх стрекоз». Сколько птиц видел Юра?
Учитель называет слово (например, пять). Ученик повторяет это слово и добавляет другое (пять, квадрат). Следующий ученик, перечислив ранее названные слова, добавляет свое (пять, квадрат, больше) и т.д. Тот, кто не сумеет повторить всех слов или перепутает их порядок - выбывает из игры. Побеждает тот, кто остается.

10.Развивающим потенциалом обладают провоцирующие задачи.

Они способствуют воспитанию одного из важнейших качеств мышления – критичности, приучают к анализу воспринимаемой информации, ее разносторонней оценке, повышают познавательную активности школьников.

Можно выделить следующие разновидности задач провоцирующего характера:

Задачи, условия которых в той или иной форме навязывают неверный ответ.
Задачи, условия которых тем или иным способом подсказывают неверный путь решения.
Задачи, вынуждающие придумывать, составлять, строить и т. п. такие математические объекты, которые при заданных условиях не могут иметь места.
Задачи, вводящие в заблуждение из-за неоднозначности трактовки терминов, словесных оборотов, буквенных или числовых выражений.

Рассмотрим примеры.

1. Сколько граней имеет новый шестигранный карандаш ?

Навязывается ответ: "6 граней", но он неверный, так как помимо 6 боковых граней у нового карандаша есть еще 2 торцевые грани. Правильный ответ: «8 граней»

2. Сколько цифр потребуется, чтобы записать двенадцатизначное число?

Навязывается ответ: "12 цифр", но это не так, поскольку десятичная система счисления обходится всего лишь десятью цифрами. Правильный ответ: "Двенадцатизначное число можно записать с помощью одной, двух, трех, четырех, пяти, шести, семи, восьми, девяти, десяти цифр".

3. Какое из следующих утверждений истинно ?

а) Четырехугольник, диагонали которого делятся точкой пересечения пополам и взаимно перпендикулярны, является прямоугольником.

б) Четырехугольник, диагонали которого делятся точкой пересечения пополам и равны, является ромбом.

в) Четырехугольник, диагонали которого взаимно перпендикулярны и равны, является квадратом.

Чаще всего учащиеся выбирают утверждение в), хотя все утверждения ложны. Правильный ответ: "Никакое".

4. Какое простое число следует за числом 200?

Напрашивается ответ: 201, ведь это число следующее — за числом 200. Но этот ответ неверен, так как число 201 — составное. На самом деле искомое число 211.

5. Что больше, число а или число 2а?

Обычно учащиеся отвечают: "2а", ведь, чтобы получить 2а, нужно а умножить на 2. Но при отрицательных значениях а справедливо обратное неравенство.

Правильный ответ: "Неизвестно".

6. Функция у = k/х является возрастающей или убывающей на каждом из промежутков (- ; 0) и (0; + )?

Напрашивается ответ: "убывающей". Он неверен, так как при отрицательных значениях к функция возрастает и на промежутке (- ; 0), и на промежутке

(0; + ). Правильный ответ: "Не определено".

7. Сколько натуральных делителей у числа 2 • 3?[Четыре.]

8. Что больше sina или sin2a? [Heопределено.]

9. Что легче: пуд пуха или пуд железа? [Равны.]

10. Одно яйцо сварится вкрутую в кипящей воде за 5 мин. За сколько минут сварятся 2 яйца? [За 5 мин.]

11. Сколько получится десятков, если два десятка умножить на три десятка? [60 десятков.]

12. Сколько натуральных чисел заключено между 300 и 700? [399.]

Повторение любой темы полезно завершать уроком, в котором основное внимание уделяется приобщению школьников к творческой деятельности.

Конечно, решение любой задачи — это прежде всего творчество, и кажется, что чем сложней задача, тем больше умственных усилий она требует и тем лучше служит развитию учащихся. Но это расхожее мнение опровергается учительской практикой. Учителя знают, что урок нельзя строить на одних только сложных заданиях, которые оказываются обычно непосильными для доброй половины класса. Настоящее обучение, вовлекающее в творческую работу весь класс, проходит именно на легком материале. Но этот материал должен быть подан разнообразно не столько в математическом, сколько в методическом плане. Под методическим разнообразием имеется в виду следующее: формулировка задачи должна содержать конфликт, который виден учащемуся сразу, без обращения к математической стороне вопроса.

К задачам такого рода часто относят следующие:

задачи, где предлагаются ошибочные рассуждения или нереальные конфигурации и требуется найти ошибку и исправить ее;
задачи, в которых по предлагаемым данным нужно отыскать все, что возможно (т.е. учащиеся вынуждены сами формулировать цели своей работы);
задачи, нацеленные на перестраивание условия путем отказа от избыточной информации.

Применение задач указанных видов при повторении тем «Четырехугольники и теорема Пифагора»

Задача 1. Найдите ошибки на рис. 1, а—г.

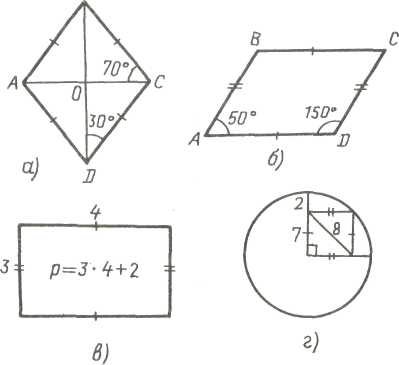
Рассмотрев рис. 1, учащиеся установят, что треугольники ВОС и DOC равны и, значит, угол DCO составляет 70°, а тогда угол COD равен 80°, что противоречит перпендикулярности диагоналей ромба. Но можно рассудить иначе: применение свойств диагоналей ромба противоречит теореме о сумме углов треугольника.

На рис. 1, г ошибочно показаны неравными смежные стороны квадрата и неправильно указана его диагональ. Это один из самых трудных случаев, поскольку здесь скрыты сразу две трудности, и одна из них графического плана. В предыдущих заданиях ребята встречались с ошибками лишь метрического характера: или с неправильно измеренными углами параллелограмма (рис. 1, б), или с ошибочно подсчитанным периметром (рис. 1, в).

Задача 2. Определите вид треугольников на рис. 2, а, б. Узнайте о них все, что возможно. Прежде всего учащиеся должны понять, что на рис. 2, а дан равносторонний треугольник, имеющий три угла по 60°. Отсюда остается сделать простейшие логические шаги до нахождения длины отрезка АС, а затем периметра треугольника ABC. По рис. 2, б ребята вычислят второй острый угол, гипотенузу, второй катет, а затем смогут найти периметр и площадь данного треугольника.

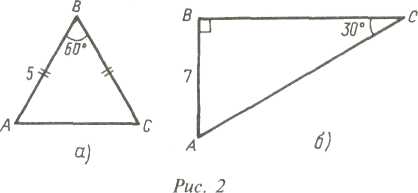
Как видим, задания нетрудные. Но все дело в том, что этих заданий учащимся никто непосредственно не предлагает. Они сами ставят перед собою маленькие цели, продвигаясь в том порядке, какой им кажется наиболее разумным. Вот так и оттачивается то, что в дальнейшем сложится в умение находить верный путь решения.

Конечно, неплохо было бы, если некоторые задачи из предлагаемых обучающимся были практико-ориентированными. Не известна ли вам такая задача?

Больному прописано лекарство, которое нужно пить по 0,25г 2 раза в день в течении 20 дней. Лекарство продаётся в упаковках по 12 таблеток по 0,25г. Какое наименьшее количество упаковок хватит на весь курс лечения?

1) 2 × 20 = 40

2) 40 : 12 = 3,333… 3,333… округляем до 4 штук, так как целостность упаковки не может быть нарушена.

Ответ: 4 упаковки.

Отдельно хочется сказать об использовании старинных задач на уроках математики. Очень веский аргумент в пользу того, что математику нужно учить не только для того, чтобы сдать зачет, написать контрольную работу или успешно сдать ЕГЭ, а, прежде всего, для того, чтобы быть образованным человеком. Сейчас существует огромный выбор книг такой направленности.

Если же говорить об учебниках, то мне посчастливилось поработать и уже выпустить параллели классов, занимавшихся по таким учебникам, в которых авторами уже предусмотрены развивающие задания всех названных ранее видов. Это УМК «Математика. Арифметика. Геометрия. 5 класс» линии «Сферы» со своим электронным приложением, содержащим более 1500 ресурсов, объединённых в рубрики:

флеш-демонстрации;виртуальные лаборатории;интерактивные модели;

интерактивные упражнения;математический кружок;игры и головоломки;тренажёры; тесты;

и тетрадью- тренажером с заданиями по видам учебной деятельности: работаем с текстом;

выполняем упражнения; находим закономерности; анализируем и рассуждаем.

И УМК по геометрии Смирновых для 7-9 и 10-11 классов, который сопровождается материалами на сайте https://geometry2006.narod.ru/ .

Рекомендации учителям, работающим с одаренными детьми:

Не занимайтесь наставлениями, помогайте детям действовать независимо, не давайте прямых инструкций относительно того, чем они должны заниматься.

Не сдерживайте инициативы и не делайте за них то, что они могут сделать самостоятельно.

Научите школьников прослеживать межпредметные связи и использовать знания, полученные при изучении других предметов.

Приучайте детей к навыкам самостоятельного решения проблем, исследования и анализа ситуации.

Используйте трудные ситуации, возникшие в школе или дома, как область приложения полученных навыков при решении задач.

Помогайте детям научиться управлять процессом усвоения знаний.
Литература

1. Беляева Н., Савенков А. И. Одаренные дети в обычной школе. // Народное образование.

– 1999.– № 9.

2. Шумакова Н.Б. Обучение и развитие одаренных детей. // М.: - 2004.

3. Гусев В.А., Комбаров А.П. Математическая разминка //М.: Просвещение. - 2005

4.https://geometry2006.narod.ru/

5.https://shkolapifagora.my1.ru/

6.https://metaschool.ru/