Разработка урока математики «Подготовка к егэ. Задачи С6»
 Скачать 20.93 Kb.
|
| Муниципальное образовательное бюджетное учреждение Средняя общеобразовательная школа села Амзя ГО г. Нефтекамск РБ Разработка урока математики «Подготовка к ЕГЭ. Задачи С6» Учитель: Новосёлова Лидия Евгеньевна Цели: отработка навыков решения задач ЕГЭ (С6); воспитание творческого подхода к решению задач типа С6. Ход урока:
- вспомнить понятия натурального и целого, рационального и иррационального числа; - определение модуля числа; - понятие «взаимно-простые числа». 2. Решение задач. Задача 1. Если к десятичной записи натурального числа а приписать справа запятую, а потом некоторый бесконечный набор цифр, то получится десятичная запись такого иррационального числа с, что (2с - 3)² = 3а² – 12с + 46. Найдите все возможные значения числа с. Решение. По условию задачи с = а + в, где 0< в <1. Так как в = с – а, то 0 < с – а < 1, а < с < а + 1. Выразим с через а из условия (2с - 3)² = 3а² - 12с + 46. 4с² - 12с + 9 = 3а² - 12с + 46, 4с² = 3а² + 37, │с│ = √(3а² + 37) /2, с > 0, с = √(3а² + 37) /2. Имеем а<√(3а² + 37)/2<а+1, а ϵ Ν. 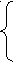 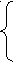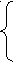√ 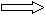 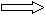(3а² + 37) > 2а, 3а² + 37 > 4а², а² < 37,√(3а² + 37) < 2а + 2; 4а² +8а +4 >3а² + 37; а² + 8а – 33 > 0; 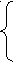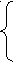│ 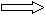а │<√ 37, │а│<√37, 3 < а < √37.(а - 3)(а + 11) > 0; а > 3 или а < - 11, Учитывая, что а – натуральное число, получаем а = 4; 5; 6. При а =4, с = √(3·4² + 37)/2 = √85/2; а = 5, с = √(3·5² + 37)/2 = √112/2 = 2√7; а =6, с = √(3·6² + 37)/2 = √145/2. Ответ: √85/2; 2 √7; √145/2 . Задача 2. Найти все пары взаимно-простых чисел а и в(а < в), таких, что если к нулю приписать справа через запятую десятичную запись числа в, то получится десятичная запись числа (в – 2а)/а. Решение. в/10ⁿ = (в – 2а)/а; в/10ⁿ = в/а – 2 (*). Так как в десятичной записи всего n цифр, то целая часть в/10ⁿ = 0, тогда целая часть в/а = 2. По определению целого числа в= 2а + с (**), где с < а. По условию а и в – взаимно – простые числа, тогда НОД (а,в) = 1, тогда и НОД (а,с) = 1. Применим (**) к (*), получаем: (2а + с)/10ⁿ = с/а; (2а + с)а = 10ⁿ · с. Так как НОД(а,с) = 1, то чтобы выполнялось полученное равенство, необходимо, чтобы (2а + с) делится на с, тогда, так как с делится на с, 2а делится на с. Но так как а и с взаимно – простые , то а должно делится на с и 2 делится на с, тогда возникают два случая:
2а² + а = 10ⁿ; n = 1: 2а² + а = 10; а = 2 или а = - 2,5; а = 2, тогда в = 2а +1 = 5. 2) с =2: (2а + 2)а = 2·10ⁿ; (а + 1)а = 10ⁿ . Получили слева – произведение двух последовательных чисел, тогда этот случай нам не подходит. Ответ: одна пара – (2;5). 3. Итог : Задача на дом. Если к десятичной записи натурального числа а приписать справа запятую, а потом некоторый бесконечный набор цифр, то получится десятичная запись такого иррационального числа с, что 2с² + с = 20а + 10. Найдите все возможные значения числа с. |