Рахмеева Л. А. (учитель математики)
 Скачать 44.17 Kb. Скачать 44.17 Kb.
|
| Рахмеева Л.А. (учитель математики) Грашина Ю.В. (учитель нач. классов) Проблема непрерывности обучения на уроках математики в 3-м и 5-м классах. Проблема непрерывности и преемственности образования всегда была одной из самых насущных и важных задач. Использование интегрированных уроков математики позволяет облегчить процесс адаптации учащихся начальных классов при переходе их в среднее звено школы, при этом формируются основные общеучебные умения и навыки, без которых школьники не смогут успешно учиться в 5-м классе. Непрерывность обучения – это отсутствие «разрывов между всеми этапами обучения, когда на каждом этапе ребенок активно работает, ему интересно, он с удовольствием идет в школу, а при переходе с одной ступени обучения на другую ему не говорят: «Забудь, как ты это делал раньше…». И.Г. Песталоцци утверждал, что процесс обучения должен быть построен таким образом, чтоб, с одной стороны, разграничить между собой отдельные предметы, а с другой – объединить в нашем сознании схожие и родственные, внося тем самым огромную ясность в наше сознание и после полного их уточнения повысить до ясных понятий. Учителя, которые планируют включить в свою педагогическую деятельность проведение интегрированных уроков, должны учитывать затруднения, которые могут при этом возникнуть. Во-первых, следует просмотреть программу уроков, которые предлагаются для изучения в 5-м классе. При этом нужно не забывать, что цель урока должна быть направлена на более глубокое изучение материала или его повторения, направленное на практическое подкрепление теоретических знаний, что необходимо для лучшего усвоения материала. Во-вторых, если урок готовиться 2 учителями, то при составлении конспекта урока следует четко распределить количество времени, отводимое каждому педагогу и проанализировать этапы объяснения материала и его закрепления каждым из педагогов. В-третьих, следует обратить особое внимание на организацию интегрированного урока: тщательно продумать расположение необходимого оборудования и его использование; продумать формы организации практической работы обучающихся; заранее разложить на столах необходимый раздаточный и рабочий материал. Все это позволяет более рационально использовать время урока. В-четвертых, не стоит забывать, что проведение интегрированных уроков требует от педагогов тщательной подготовки к уроку. Учителя должны строго придерживаться конспекта урока, тщательно продумать формы и методы работы на уроке. Такие уроки являются непривычными не только для учащихся, но и для учителя, а следовательно, от учителя требуется умение импровизировать. Современные технологические приемы помогают учителям расширить рамки педагогических возможностей при подготовке к интегрированным урокам. На таких уроках изменяется характер взаимодействия учителей с учениками с целью сделать их поведение на уроке более активным. Так при повторении и обобщении темы «Нахождение площади прямоугольников» в 3-м классе был проведен интегрированный урок математики учителем начальной школы и учителем математики средней школы. При этом были использованы возможности интерактивной доски, которые позволяли более глубоко повторить изученный материал и познакомиться с более сложными задачами, которые решаются в курсе 5-го класса. Рассмотрим основные этапы такого урока. В начале урока учащимся сообщается тема, цели и задачи урока, а также рассказывается об уроках и требованиях, которые предъявляются ученикам 5-го класса. На следующем этапе учитель начальной школы проводит повторение материала при помощи устного счета, в ходе которого повторяются основные формулы нахождения площади прямоугольника и квадрата, и нахождение сторон по известной площади. На 1-м слайде расположены номера задач (рис. 1), после чего при помощи инструментов доски Mimio поэтапно выдвигаются задания для учащихся (рис. 2).  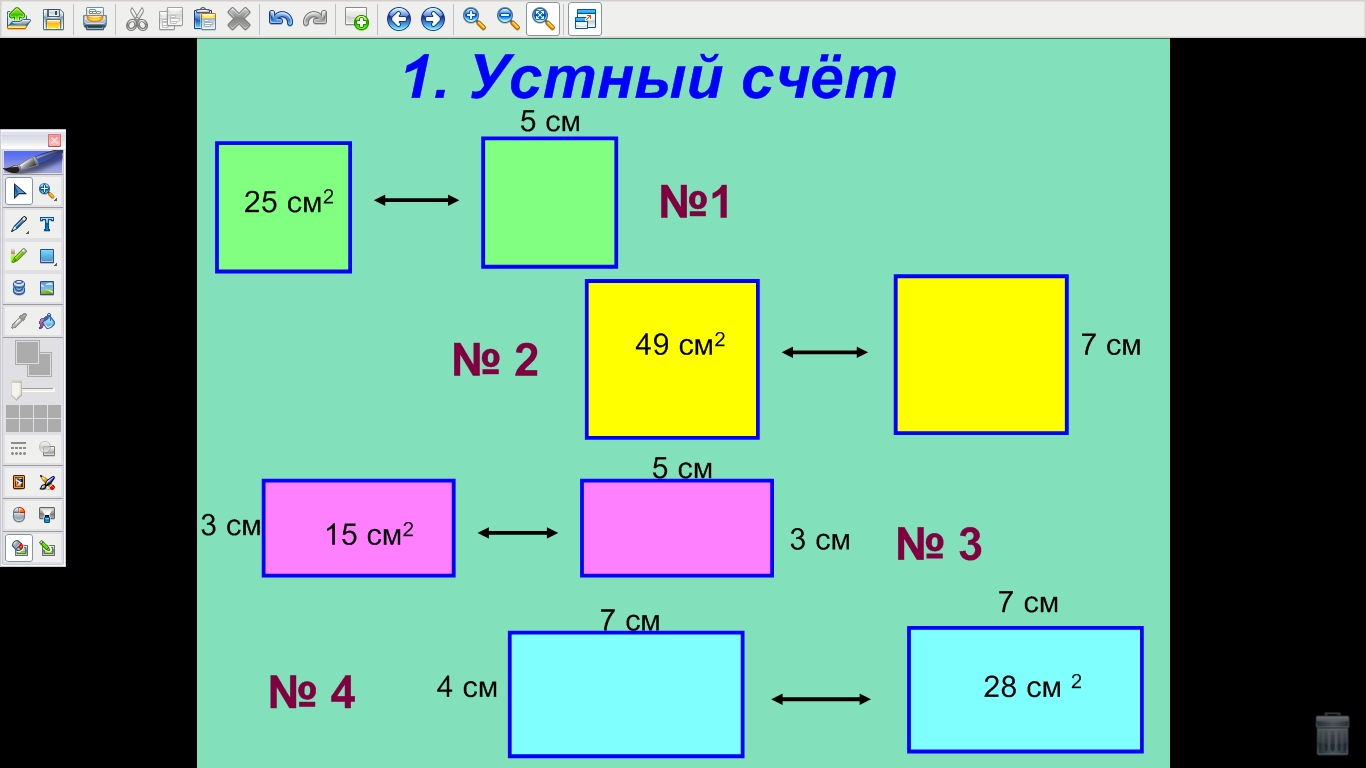 (рис. 1) (рис. 2) После повторения учитель математики ставит перед учащимися усложненные задачи на нахождение площади «сложных» фигур. Этот этап подразумевает знакомство учащихся со способом нахождения площади таких фигур при помощи разбиения их на прямоугольники и вычисления площади при помощи подсчета клеток. На слайде предлагается учащимся две задачи на нахождение площади фигур (рис. 3). Идет обсуждение способа нахождения площади, а затем предлагается решение этой задачи при помощи разбиения фигуры на прямоугольники (рис. 4). 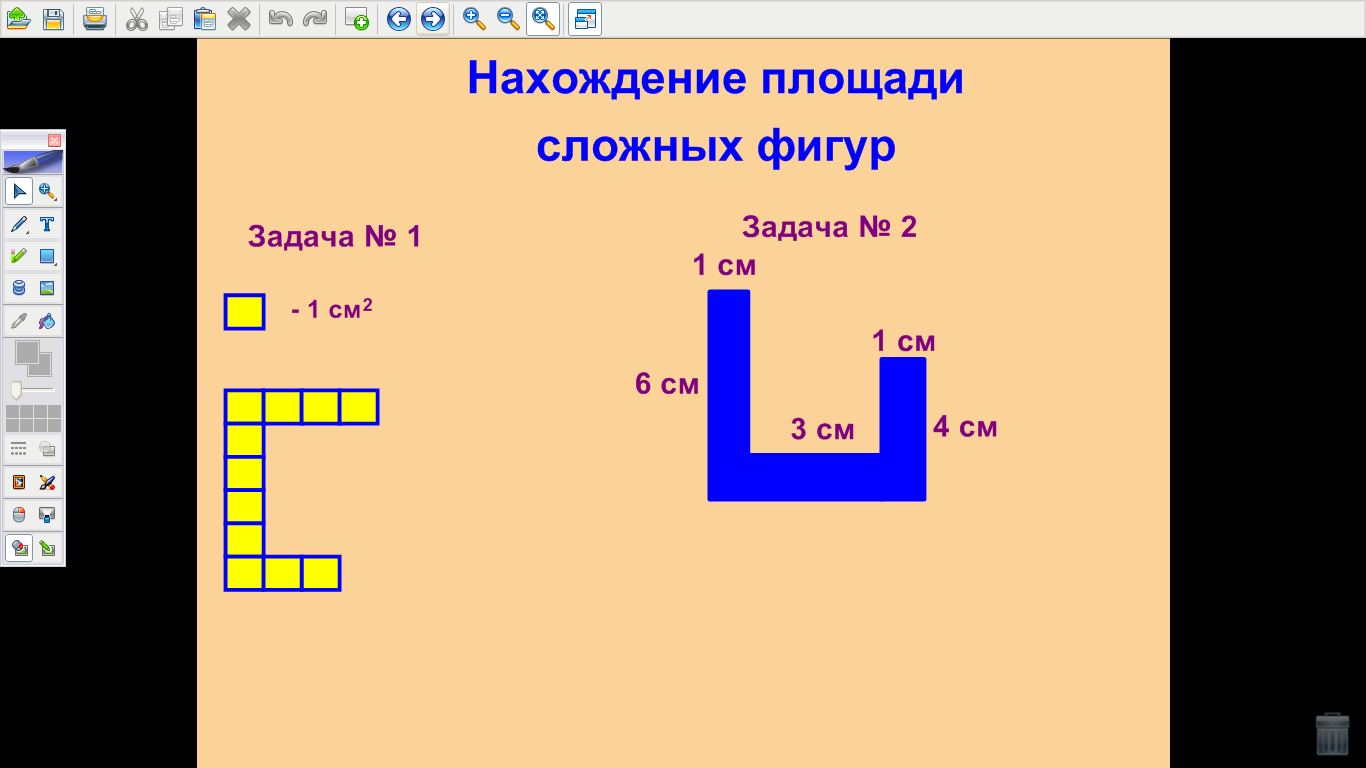  (рис. 3) (рис. 4) На этапе закрепления формулы нахождения площади прямоугольника учащимся предлагается работа с задачей, которая выполняется по действиям. Каждое действие обсуждается и при помощи инструментов доски Mimio выполняются учащимися. Задача. Буратино на участке, который имеет форму прямоугольника со сторонами 9 м. и 7 м., построил дом с размерами 3 м. и 2 м., а остальную площадь засеял газоном. Найти площадь газона. Решение. Учащиеся обсуждают задачу и намечают порядок выполнения действий. Первым действием они находят площадь участка (рис. 5). Вторым действием находят площадь дома (рис. 6). Третьим действием вычисляют площадь газона (рис. 7).  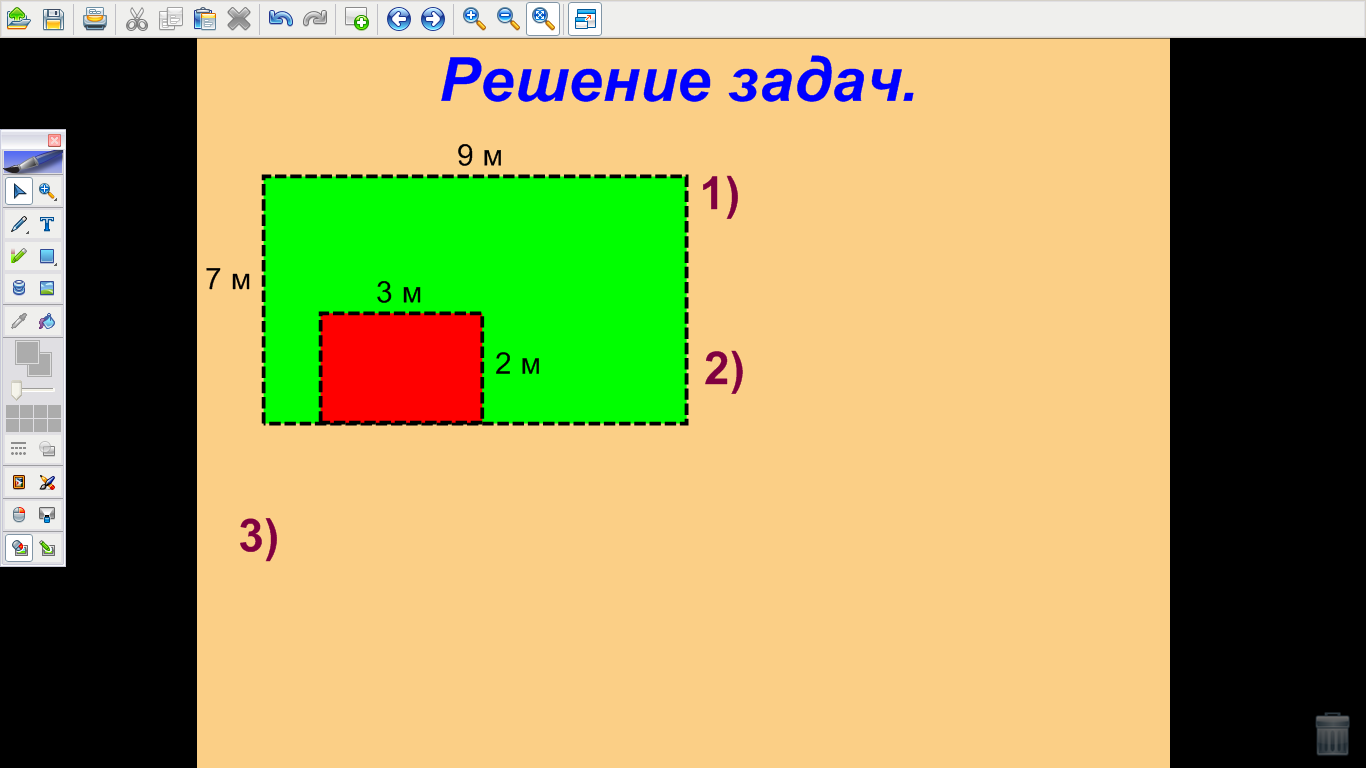 (рис. 5) (рис. 6)  (рис. 7) (рис. 7)На заключительном этапе урока учитель математики сообщает учащимся еще об одном способе нахождения площадей сложных фигур при помощи палетки. Учащимся предлагается рисунок сложной фигуры (рис. 8), а затем с помощью инструментов доски Mimio на нее накладывается палетка и учитель вместе с учащимися находит площадь этой фигуры (рис. 9). После чего учитель предлагает учащимся при помощи заранее заготовленных и розданных детям палеток и рисунков найти их площади. Учащиеся выполняют эту работу и сдают рисунки на проверку своему учителю. Учитель проверяет и на следующем уроке выставляет оценки. 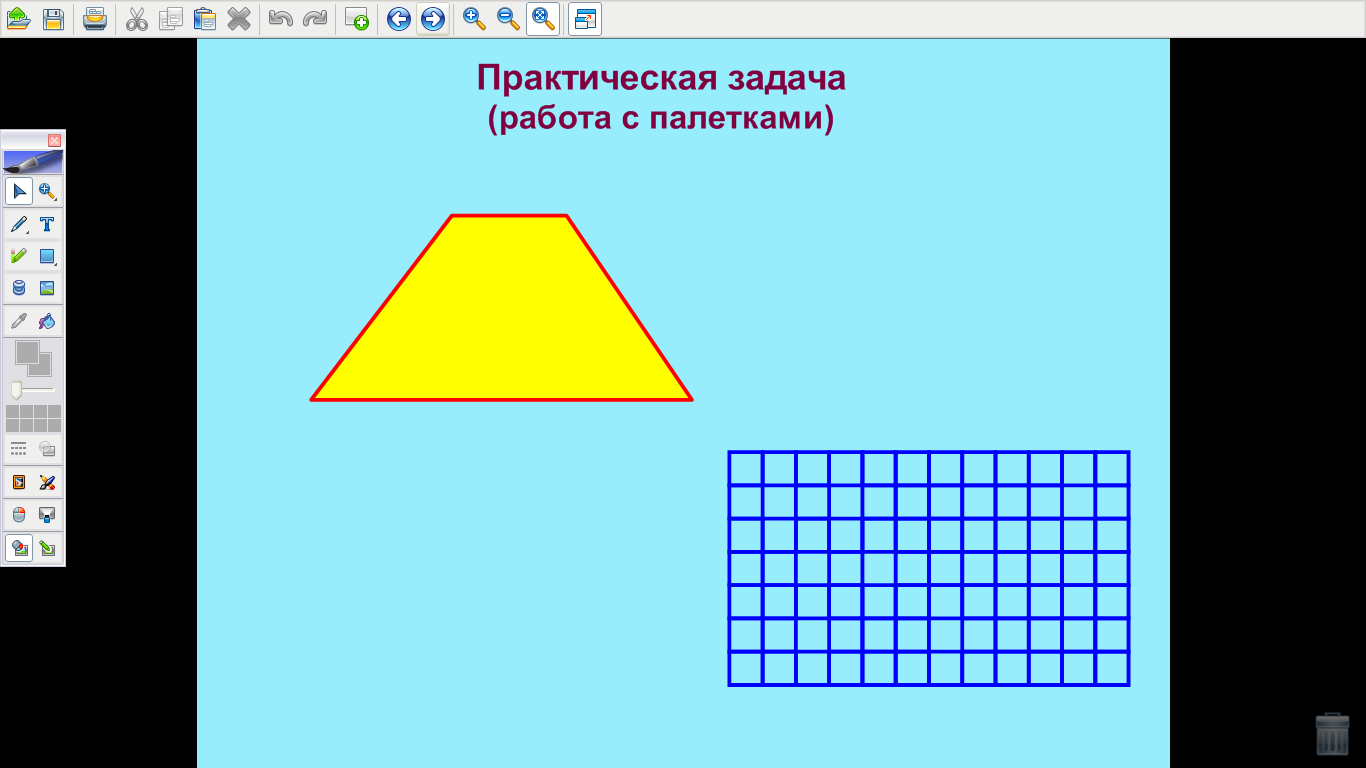 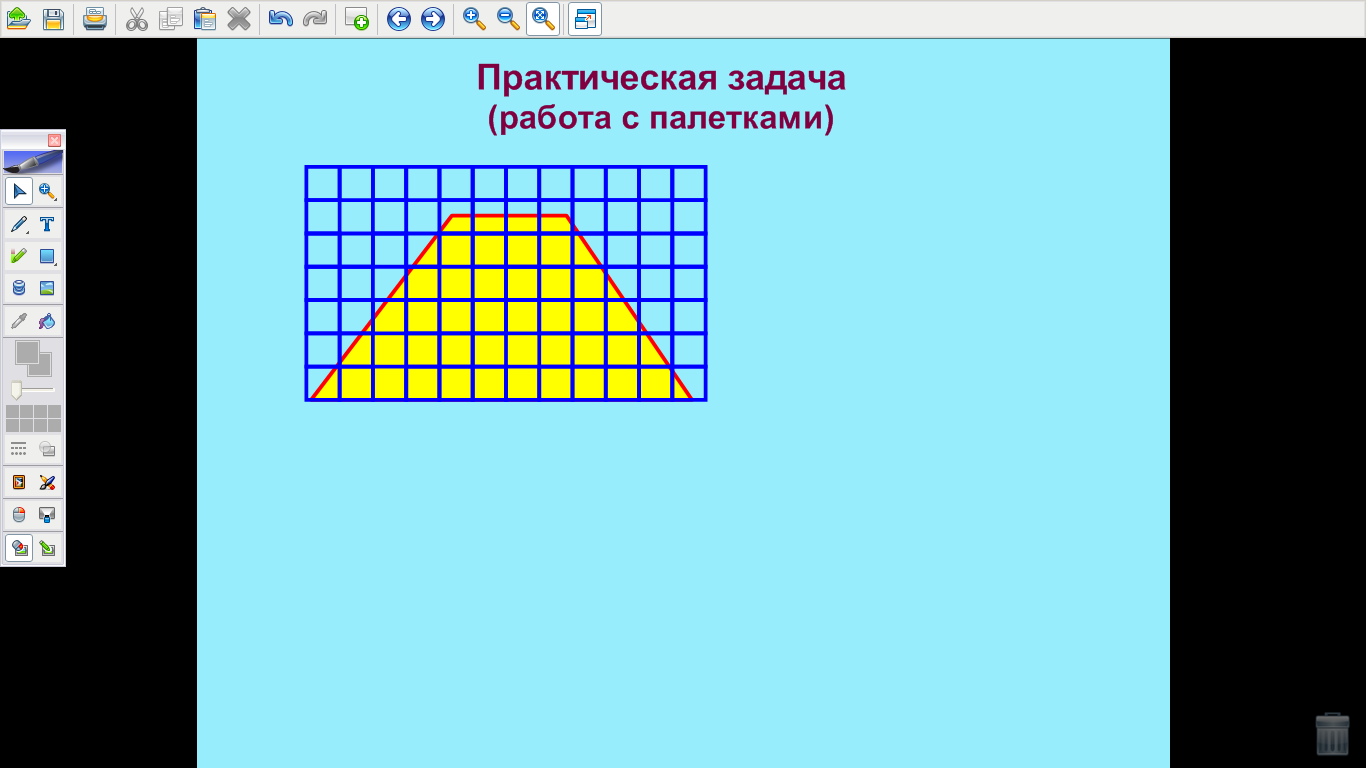 (рис. 8) (рис. 9) Таким образом, на этом уроке были реализованы следующие задачи: - повторение и обобщение темы «Нахождение площадей прямоугольников»; - умение определять понятие площади, устанавливать связь между нахождением площади и сторон; - умение строить логические рассуждения и делать выводы; - знакомство с новыми способами нахождения площади сложных фигур; - формирование готовности и способности обучающихся к восприятию учебного материала в следующем классе. |