Работа с одаренными детьми на уроке математики

Название	Работа с одаренными детьми на уроке математики
Дата	27.02.2016
Размер	74.86 Kb.
Тип	Документы

Работа с одаренными детьми на уроке математики.
« Три пути ведут к знанию:

путь размышления - это путь самый благородный,

путь подражания - это путь самый легкий

и путь опыта - это путь самый горький».

( Конфуций)
Развитие учащихся во многом зависит от той деятельности, которую они выполняют в процессе обучения. Если деятельность репродуктивная – ученик получает готовую информацию, воспринимает ее, понимает, запоминает, а затем воспроизводит. Цель такой деятельности – формирование знаний, умений и навыков.

Если деятельность продуктивная – происходит активная работа мышления, связанная с логическими операциями анализа, синтеза, сравнения, аналогии, обобщения. Задумываясь над основанием собственных умений (рефлексируя), ребенок овладевает обобщенными способами действий, лежащими в основе этого умения, и тем самым приобретает знания, которые может конкретизировать при решении целого класса частных задач. В общем случае появлению конкретных знаний предшествует овладение методом получения этих знаний.

«Кто приобретает знания, но не пользуется ими, подобен тому, кто пашет, но не сеет».

("Круг чтения").

В своей работе с одаренными детьми по математике я вижу главную задачу не в раскрытии принципов действия, решение задачи ради точного ответа, а ради способа его получения, ради логических рассуждений на пути к нему. Я подбираю задания, выходящие за рамки изучаемых понятий по годам обучения, задания, требующие нестандартного подхода к их решению.

Задания подбираются таким образом, чтобы их можно было систематизировать по общему способу их решения и представить в виде модели (знаковой, геометрической, диаграммы, алгоритма действий и т.д.)

Получив пятый класс, я, как все учителя, выявляю одаренных детей, начинаю кропотливую работу по развитию способностей детей с использованием интерактивных технологий, ведь все дети, в основном, способны в той или иной области. И развитие одаренности в одной области влекут в той или иной мере развитие способностей в других областях, хотя и неравномерно (как бы нам этого не хотелось).
Эта работа идет в трех направлениях. Постоянный подбор задач, которые решаются различными способами, выделяя оптимальный способ. Решение задач повышенной сложности в освободившееся время на уроках и внеурочное время. Проведение модульной работы с классом, которая выявит способных «раскрутиться». Привлечение детей ко всяким предметным олимпиадам, турнирам, играм.
В 7 – 8 классах активно работаю на уроках и во внеурочное время с группой не более 15 человек, иногда индивидуально, по прохождению отдельных тем для подготовки детей к профильному обучению математике. После 8 класса стараюсь «пристроить» учеников в «Летнюю гуманитарно-математическую школу» -уникальное место для веселого, полезного и умного отдыха на летних каникулах.

В 8, 9 классах начинаю индивидуальную работу по подготовке к НПК. Эта задача сложная для любого учителя, а желание детей к научной работе уже пробуждается. Вот здесь любому учителю необходима помощь Вузовских преподавателей.
Учебный процесс строю таким образом, чтобы на уроке создать максимальную комфортность, хороший рабочий микроклимат. Наряду с традиционными формами обучения используются современные образовательные технологии, которые работают на результативность:
· Уроки «Ярмарка задач» в 5 – 11 классах,
· «Урок одного уравнения » (где под моим руководством ученики находят несколько способов решения уравнения),
· «Общественные смотры знаний», математические эстафеты, викторины.
Самым продуктивным для одаренных детей является такой вид работы, как «Ярмарки задач», на которых представляются решения изящных задач, полученных заранее на дом. Задачи подбираю таким образом, что они решаются различными способами или имеют нестандартный подход к решению.

При завершении каждого раздела математики использую карточки для одаренных детей с задачами повышенной сложности при написании контрольной работы с последующим их разбором.

Под моим руководством дети используют на уроках фрагменты мультимедийных презентаций своих творческих работ.

Самым эффективным в работе с одаренными детьми считаю такой вид деятельности, как «Урок одной задачи», где ребята могут показать различные подходы в решении задачи.

Решение одной геометрической задачи несколькими способами.

Ниже предлагаю девять решений одной красивой геометрической задачи.

З а д а ч а. На гипотенузе АВ прямоугольного треугольника АВС построен квадрат ABDE в той полуплоскости от прямой АВ, которой не принадлежит треугольник АВС. Найти расстояние от вершины С прямого угла до центра квадрата, если катеты ВС и АС имеют соответственно длины a и b.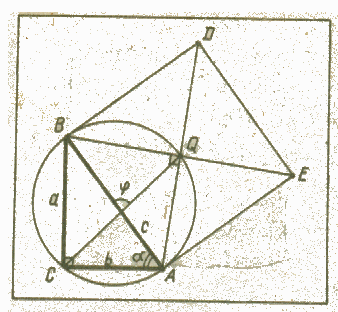

Рис.3

Решение 1 (по теореме синусов).

Пусть Q - центр построенного квадрата(рис.3). Так как угол AQB прямой, то точка Q лежит на описанной около треугольника АВС окружности. Ее диаметром служит гипотенуза АВ. Из треугольника AQC по теореме синусов имеем: СQ = АВsin(α+45°), где α – величина угла ВАС. Далее получаем:
CQ= c(sinαcos45°+cosαsin45°) =

) =

, где с = АВ. Итак, искомое расстояние CQ равно

.
Решение 2 (по теореме косинусов).
Из того же треугольника AQC по теореме косинусов находим:
CQ² = b² + AQ² – 2b∙CQcos (α+45°).
Рассмотрим треугольник AQB, который является прямоугольным и равнобедренным (BQ=QA). По теореме Пифагора находим, что AQ² =

c². Тогда

CQ² = b² +

c² – 2b∙

∙

(

) = b² +

(a² + b²) – b² + ab =

(a +b)², СQ =

Решение 3 (по теореме Птолемея).

Во вписанном в окружность четырехугольнике сумма произведений длин противоположных сторон равна произведению длин диагоналей (теорема Птолемея). Поэтому для вписанного четырехугольника AQBC имеем:
a∙AQ + b∙BQ = c∙CQ.

Но AQ = BQ =

и, следовательно,

(a + b)

= c∙ CQ, откуда CQ =

.
Решение 4 (методом площадей).
Сумма площадей треугольников АВС и ABQ равна площади четырехугольника AQBC:

ab +

AQ² =

c∙CQsinφ,
где φ – величина угла между прямыми AB и CQ. Луч CQ есть биссектриса угла АСВ, так как вписанные углы ACQ и BCQ опираются на равные дуги AQ и BQ.По теореме о внешнем угле треугольника φ = α + 45°. Подставив в предыдущее равенство AQ² =

(a² + b²) и sinφ =

∙

(по решению 1), получим:

ab +

(a^{2 +}b²) = CQ∙

(a + b) и CQ =

Решение 5 (методом геометрических преобразований).

Выполним поворот около центра Q квадрата на 90°: В→А, А→А₁, С→С₁ (рис.4). Так как

А₁АС₁ =

СВА, то

САВ +

ВАА₁ +

А₁АС₁ = 180°,

и поэтому точки С,А,С₁ лежат на одной прямой. В треугольнике CQC₁ угол CQC₁ прямой (угол поворота), CQ = C₁Q, СС₁ = АС₁ = a+b. Следовательно, CQ =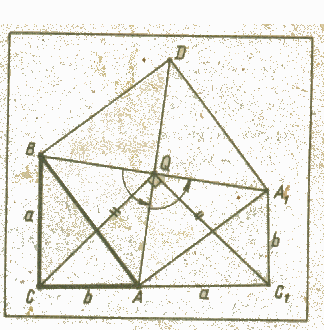

Рис.4

Решение 6 (методом координат).

Примем прямые СА и СВ за оси Ох и Оу прямоугольной декартовой системы координат. Найдем координаты х, у точки Q. Она принадлежит биссектрисе угла АСВ (по решению 4) и равноудалена от точек A(b,0) и B(0,a). Имеем систему:

х = у

(x - b)² + у² = х² + (у - а)²,
откуда 2х(b - а ) = b² – a² (подставив первое равенство во второе).

Если a ≠b, то имеем решение х = у =

.

При a = b четырехугольник AQBC является квадратом и х = у =а, т.е. координаты точки Q удовлетворяют прежнему решению. По формуле расстояния между двумя точками

CQ =

Решение 7 (векторное).

Положим

= b и

= a и выразим через эти векторы вектор

(рис.3):

(

) =

(

) +

(

) +

,

положив

= αа + βb, найдем коэффициенты α и β этого разложения, используя условия

∙

= 0 и

, которые приводят к системе уравнений:
(α

+ β

)(

) = 0,

(α

+ β

)² = (

–

)².
Поскольку

= 0, то эта система эквивалентна такой:
α

² - β

² = 0,

α²a² + β²b^{2 =}

² +

² ,
откуда α =

и β =

и, следовательно,

(

) +

(

) =

(

).

Наконец, CQ² =

(a+b)², CQ =

.
Решение 8 (методом комплексных чисел).
Введем прямоугольную декартову систему координат так же, как при решении 6. Тогда точки А,В,С будут иметь соответственно комплексные координаты b, ai, 0, причем a =

, b =

. При повороте на 90° вектор

переходит в вектор

. Этому повороту соответствует умножение на комплексное число i. Поэтому имеем равенство: (ai - q)i = b-q, где q – комплексная координата точки Q. Отсюда q =

. Находим:

CQ² = q

∙

(a+b)².

Решение 9 (чисто геометрическое).

Опишем около квадрата другой квадрат со стороной a+b. Тогда искомое расстояние, очевидно, равно половине диагонали большего квадрата.
Рассмотренные выше методы и приёмы обучения нацеливают деятельность каждого учителя на поддержку познавательного интереса своих учеников, формирование потребности и способности личности к саморазвитию, создание максимальных условий к перерастанию потенциальной одарённости в развившуюся.

В Сибири число одаренных детей в каждом возрасте составляет от 8 до 10%, а это самый высокий показатель на планете.
Использованная литература: статья «Учителю об одаренных детях(глазами психолога-консультанта)»А. Кулемзина ,

«Задача одна - решений много» Я. П. Панарин,

«Богатство интересов - залог обучаемости» К. В. Лавренович,

«Контуры дифференциации в преподавании математики» В. Н. Келбакиани,

«О технологии творческого обучения математики» Б. П. Эрдниев.

Материалы с сайтов https://cap.ru/, https://festival.1september.ru/ .