|
Рабочая программа
государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная школа № 2 с углубленным изучением отдельных предметов п.г.т.Усть – Кинельский городского округа Кинель Самарской области
РАБОЧАЯ ПРОГРАММА
элективного курса по алгебре и началам математического анализа
«Решение логарифмических уравнений и неравенств».
для 11 класса
ГБОУ СОШ № 2 п.г.т. УСТЬ-КИНЕЛЬСКИЙ
НА 2013 – 2014 УЧЕБНЫЙ ГОД
Составитель:
Старостина О.Е
Учитель математики
.
п.г.т. Усть – Кинельский 2013 г.
"Мало знать, надо и применять, мало хотеть, надо и делать". Гете
«Решение логарифмических уравнений и неравенств».
Структура программы.
1 Пояснительная записка.
2 Цели курса.
3 Задачи курса.
4 Учебно – тематический план.
5 Содержание курса.
6 Литература.
7 Приложения.
Данная программа предназначена для учащихся 11 класса, желающих успешно сдать экзамен в форме ЕГЭ и собирающихся после окончания школы поступить в высшие учебные заведения. Методы решения логарифмических уравнений и неравенств рассмотрены в учебнике для общеобразовательных учреждений « Алгера и начала математического анализа » для 10 – 11 классов. Это одна из важных тем школьного курса, но на освоение этих тем отводится мало часов, и на решение уравнений и неравенств повышенного уровня сложности времени на уроках не остаётся. При решении заданий такого уровня учащиеся приобретают первые навыки исследовательской работы. Курс призван помочь учащимся сознательно овладеть системой математических знаний и умений, достаточных для изучения смежных дисциплин, для достойной сдачи ЕГЭ и продолжения образования в ВУЗе, а также предусматривает развитие математических способностей, логического мышления, интереса к решению задач различного уровня сложности. В процессе решения логарифмических уравнений часто используются преобразования, которые изменяют область допустимых значений исходного уравнения, следовательно, могут появиться посторонние решения или могут быть потеряны решения, поэтому при решении логарифмических уравнений полезно использовать равносильные преобразования. Если при решении логарифмического уравнения можно найти корни уравнения, а потом сделать проверку, то при решении логарифмического неравенства при переходе от логарифмов к выражениям, стоящим под знаком логарифма необходимо записывать ОДЗ неравенства. При решении нестандартных задач встречаются уравнения, содержащие разнородные функции. Задания подобного типа встречаются среди экзаменационных в задачах части С. В учебнике «Алгебра и начала анализа» А. Г. Мордковича есть несколько подобных заданий, но четкого определения и метода решения данных уравнений нет. Данный курс позволит учащимся расширить и систематизировать знания о методах решения логарифмических уравнений и неравенств. Все занятия должны носить исследовательский, дифференцированный характер и включать в себя самостоятельную работу. Для обобщения, систематизации знаний учащихся и проверке умений и навыков решения задач по изученной теме проводятся два зачёта. Формы и методы работы: лекция, семинар, самостоятельная работа, индивидуальные формы работы.
Цели изучения курса:
Обобщение, систематизация и расширение методов, способов решения логарифмических уравнений и неравенств;
оказание индивидуальной и систематической помощи выпускнику при подготовке к экзаменам.
Задачи курса:
обеспечение усвоения учащимися наиболее общих приемов и способов решения логарифмических уравнений и неравенств повышенного уровня сложности;
формирование у старшеклассников аналитического и логического мышления ;
развитие умений самостоятельно анализировать и решать задачи по образцу и в незнакомой ситуации;
формирование навыков вести дискуссию, аргументировать ответы;
формирование навыков решать задания, по типу приближенных к заданиям ЕГЭ;
формирование навыка работы с научной литературой и интернетресурсами.
Планируемые результаты обучения: прошедшие курс учащиеся должны уметь решать различные виды уравнений и неравенств, распознавать их, определять метод их решения, использовать свойства функций.
Данный курс рассчитан на 17 часов. 1 час в неделю.
Учебно – тематический план.
-
№ занятия
|
Наименование тем курса
|
Количество часов
|
1
|
Актуализация базовых знаний.
|
1
|
2
|
Приведения логарифмов к одному и тому же основанию. Метод потенцирования.
|
2
|
3
|
4
|
Решение уравнений, методом логарифмирования. Метод замены переменной
|
2
|
5
|
6
|
Уравнения, содержащие переменную и в основании логарифма и в выражении, стоящем под знаком логарифма.
|
2
|
7
|
8
|
Зачётная работа 1.
|
1
|
9
|
Графические методы решения уравнений, неравенств.
|
2
|
10
|
11
|
Метод мажорант.
|
2
|
12
|
13
|
Решение комбинированных уравнений, неравенств.
|
2
|
14
|
15
|
Решение логарифмических неравенств методом интервалов.
|
2
|
16
|
17
|
Итоговое занятие. Зачётная работа 2 .
|
1
|
Содержание программы
Актуализация базовых знаний: (выполнение действий, состоящих в извлечении из кратковременной или долговременной памяти ранее усвоенного материала для его использования, расширение, углубление знаний при помощи ранее усвоенного) повторение свойств логарифмических функций; свойств логарифмов, определение логарифмического уравнения, определение логарифмического неравенства.
Приведения логарифмов к одному и тому же основанию. Метод потенцирования. Потенцировать – значит научиться освобождаться от знаков логарифмов в процессе решения. Рассмотреть методы решения логарифмических уравнений, подчеркнуть, что в процессе решения логарифмических уравнений часто используются преобразования, которые изменяют область допустимых значений (ОДЗ) исходного уравнения. Следовательно, могут появиться посторонние решения или могут быть потеряны решения. Практическое закрепление.
Решение уравнений методом логарифмирования. Метод замены переменной. Рассмотреть уравнения, которые решаются методом логарифмирования. Этим методом решаются уравнения, содержащих переменную и в основании и в показателе степени. Если, при этом, в показателе степени содержится логарифм, то обе части уравнения надо логарифмировать по основанию этого логарифма. В некоторых случаях логарифмическое уравнение можно свести к алгебрическому уравнению относительно новой переменной. Рассмотреть уравнения вида f(logax) = 0, где f(x) - алгебраическая рациональная функция. Посредством подстановки logax = t сводится к алгебраическому уравнению относительно t, f(t) = 0. Основная трудность решения задач методом подстановки заключается в том, что иногда трудно угадать вид самой подстановки и вид уравнений, где подстановку можно использовать.
Уравнения, содержащие переменную и в основании логарифма и в выражении, стоящем под знаком логарифма.
Поиски разных способов решения комбинированных уравнений и неравенств, рассмотрение всех возможных случаев, критическая оценка их с целью выделения наиболее рационального, красивого. Обратить внимание, что при решении неравенства при переходе от логарифмического неравенства к рациональному знак неравенства будет зависеть от основания логарифма и монотонности логарифмической функции.
Функционально - графический метод решения уравнений, неравенств. Повторить свойства и графики функций. Графически решением уравнения являются абсциссы точек пересечения графиков функций, заданных в уравнении.
Метод мажорант. Метод мажорант - нестандартный метод решения уравнения и неравенств. Заключается в том, что одна часть уравнения (или неравенства) ограничена сверху неким числом М, а другая часть уравнения (или неравенства) ограничена снизу этим же числом
f(x) ≤ М и g(x) ≥ М
f(x)=M и g( (x)=M
Признаком присутствия мажоранты в задаче могут быть комбинированные уравнение (или неравенство), т.е. в задании есть разнородные функции, например: логарифмическая и линейная; квадратный трехчлен и логарифмическая; тригонометрическая и логарифмическая, или вообще несколько видов.
Для того чтобы найти мажоранту нужно выполнить одно или несколько действий:
найти D(f) функции;
найти E(f) функции;
исследовать функцию на экстремум;
если функция определена на отрезке, найти наибольшее и наименьшее значения;
используется определение ограниченных функций;
преобразовывать функции, так, чтобы было проще вытащить мажоранту;
мажоранту можно найти, используя графики функций.
Решение комбинированных уравнений, неравенств. При решении комбинированных уравнений ( неравенств) приходится применять комбинации различных приёмов, преобразований, после которых оно сведётся к простейшему: линейному или квадратному. При проведении преобразований мы изменяем внешний вид уравнения (неравенства), но при этом можем изменить множество его решений. Проводимые с уравнением (неравенством) действия могут привести либо к потере корней , за счёт сужения области допустимых значений; либо к приобретению корне, за счёт расширения области допустимых значений.
Решение логарифмических неравенств методом интервалов. Нахождение области определения функции, решение неравенств по алгоритму. Алгоритм решения неравенств методом интервалов.
Собираем все слагаемые в левой части неравенства .
Приводим слагаемые к общему знаменателю. В левой части неравенства получаем дробь, знаменатель которой уже разложен на множители. В правой части стоит нуль.
Раскладываем числитель полученной дроби на множители.
Отмечаем на числовой прямой нули числителя и знаменателя. Нули знаменателя выколоты. Нули числителя выколоты, если неравенство строгое, и закрашены, если неравенство нестрогое.
Расставляем знаки на полученных интервалах. Если множитель х-х0 стоит в нечётной степени, то при переходе через х0 знак меняется. . Если множитель х-х0 стоит в чётной степени, то при переходе через х0 знак не меняется.
Записываем ответ. Если при переходе через закрашенную точку знак не меняется и точка оказалась внутри промежутка решений, то это число «погложается» этим промежутком. Если закрашенная точка не находится внутри промежутка решений, то это число является решением.
Итоговое занятие. Зачётная работа.
Литература.
Программа: И.И. Зубарева, А.Г. Мордкович Алгебра и начала математического анализа.10-11классы. – М.: Мнемозина, 2009.
Мордкович А.Г. Алгебра и начала анализа 10 - 11 Учебник. Москва, Мнемозина, 2011г.
Мордкович А.Г. и др. Алгебра и начала анализа. Задачник10 - 11. Москва, Мнемозина, 2011г.
Глинзбург В. И. Алгебра и начала математического анализа 11. Контрольные работы для общеобразовательных учреждений (базовый уровень) под ред. Мордковича А.Г.. Москва, Мнемозина, 2012г.
Александрова Л.А. Алгебра и начала математического анализа 11. Самостоятельные работы/ под.ред. Мордковича. Москва, Мнемозина, 2009г.
Денищева Л.О., Корешкова Т.А. Алгебра и начала анализа. Тематические тесты и зачеты / под.ред. Мордковича. Москва, Мнемозина, 2010г.
А.Г. Мордкович Алгебра и начала анализа.10-11.Методическое пособие для учителя. М:Мнемозина, 2010г.
Рурукин А.Н., Масленникова И.А. Поурочные разработки по алгебре и началам анализа. 11 класс. – М.: ВАКО, 2011
Тренировочные материалы для подготовки к ЕГЭ по математике. Самара: ГОУ СИПКРО, 2012 Составители : С.В.Богатырев, А.А. Максютин и др.
ЕГЭ – 2012. Математика: типовые экзаменационные варианты: 30 вариантов / под. Редакцией А.Л. Семенова, И. В. Ященко. – Национальное образование, 2012.
Саакян С.М. Задачи по алгебре и началам анализа: Пособие для учащихся 10- 11 кл. общеобразовательных учреждений. М.: Просвещение,2003.
Интернетресурсы
https://math.md/school/praktikum/logr/logr.html
https://raal100.narod.ru/index/0-268
Приложение 1.
Приведения логарифмов к одному и тому же основанию. Метод потенцирования.
а) 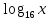 + +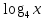 + +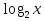 =7; =7;
б) 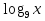 + + 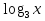 = 5; = 5;
в) 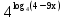 < 16; < 16;
г)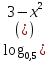 + 1< + 1< 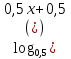 ; ;
д) 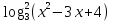 – 3 – 3 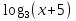 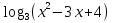 -2 -2 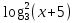 =0 =0
Методом логарифмирования. Метод замены переменной.
а)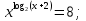
б)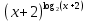 = 4(х+2); = 4(х+2);
в) 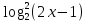 + + 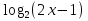 – 2 =0; – 2 =0;
г) 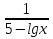 + + 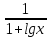 < 1; < 1;
д) 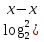 2 +2) +3 2 +2) +3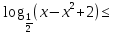 -2; -2;
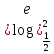 х + х + 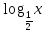 – 2 – 2 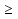 0. 0.
Уравнения и неравенства, содержащие переменную и в основании логарифма и в выражении, стоящем под знаком логарифма
а) 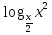 - 1 - 1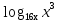 + +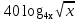 =0; =0;
б) log3х+7 (9 + 12х + 4х2) + log2х+3 (6х2 + 23х + 21) = 4;
в) log x+1(x3 - 9x + 8)log x-1(x + 1) = 3;
г) log2x(x2 - 5x + 6) < 1;
д)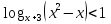 . .
Графические методы решения уравнений.
а) log5(x + 2) = 4 – x;
б) 2x = 9 - log3x;
в)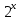 = = 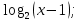
г) Определите число корней уравнения 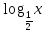 = - х2 + 2х -1 = - х2 + 2х -1
Метод мажорант.
a) log2(6x - x2 - 5) = x2 - 6x + 11;
б) log2(x2 + 1) - log2x = 2x - x2 ;
в) log3 (8 + 2х – х2) = 2х-1 + 21-х ;
г) 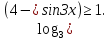
Решение комбинированных уравнений, неравенств.
а)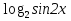 = = 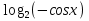 ; ;
б) lg cos x + log0,1 sin 2 x = lg 7;
в)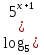 – 20) = х; – 20) = х;
г) 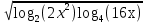 = = 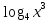 ; ;
д) 4log16 (cos 2x) + 2log4 (sin x) + log2 (cos x) +3 < 0;
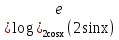 < 0 ; < 0 ;
ж)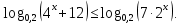
Решение логарифмических неравенств методом интервалов.
а) 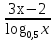 < 0; < 0;
б) 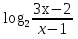 +3 +3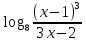 < 2 < 2
в) 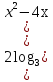 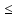 1; 1;
г)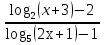 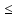 1; д) 1; д) 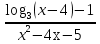 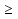 0 0
|
|
|
 Скачать 126.48 Kb.
Скачать 126.48 Kb. +
+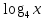 +
+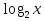 =7;
=7;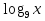 +
+ 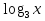 = 5;
= 5;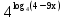 < 16;
< 16;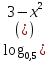 + 1<
+ 1< 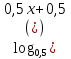 ;
;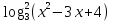 – 3
– 3 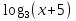
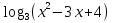 -2
-2 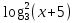 =0
=0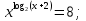
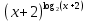 = 4(х+2);
= 4(х+2);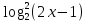 +
+ 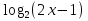 – 2 =0;
– 2 =0;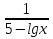 +
+ 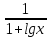 < 1;
< 1;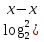 2 +2) +3
2 +2) +3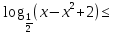 -2;
-2;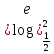 х +
х + 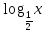 – 2
– 2 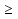 0.
0.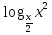 - 1
- 1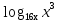 +
+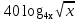 =0;
=0;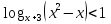 .
.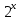 =
= 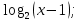
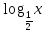 = - х2 + 2х -1
= - х2 + 2х -1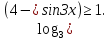
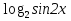 =
= 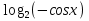 ;
;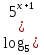 – 20) = х;
– 20) = х;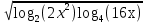 =
= 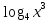 ;
;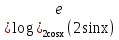 < 0 ;
< 0 ;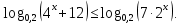
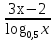 < 0;
< 0;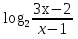 +3
+3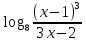 < 2
< 2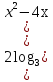
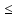 1;
1;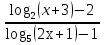
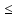 1; д)
1; д) 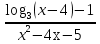
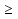 0
0