|
Формы занятий
Урок беседа с элементами лекции;
Урок решение задач;
Урок самостоятельная работа;
Урок обобщения, систематизации и корректировки знаний, умений, навыков;
Урок игра;
Урок практикум
Урок- лабораторная;
Урок семинар;
Урок зачет;
Урок дискуссия;
Уроки-презентации;
Урок- КВН.
Планируемые результаты обучения.
Знать/понимать
Существо понятия математического доказательства, приводить примеры доказательств.
Существо понятия алгоритма, приводить примеры алгоритмов.
Как используются математические формулы, уравнения и неравенства, примеры их применения для решения математических и практических задач.
Как математически определенные функции могут описывать реальные зависимости, приводить примеры таких описаний
Как потребности практики привели математическую науку к необходимости расширения понятия числа.
Вероятностный характер многих закономерностей окружающего мира, примеры статистических закономерностей и выводов.
Каким образом геометрия возникла из практических задач землемерия, примеры геометрических объектов и утверждений о них, важных для практики.
Смысл формализации, позволяющий решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при формализации.
Арифметика
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе с использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычислений с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
Уметь
составлять формулу по условию задачи; осуществлять числовые подстановки и выполнять соответствующие вычисления в формулах, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через другую;
применять свойства арифметических корней для вычисления значений и преобразования числовых выражений, содержащих корни;
решать линейные, квадратные и рациональные уравнения, сводящиеся к ним, системы двух уравнений, линейные и несложные нелинейные;
решать линейные и квадратные неравенства и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа на координатной прямой и точки с заданной координатой на координатной плоскости; изображать множество решений неравенства на координатной прямой;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значение функции по ее аргументу, значение аргумента по значению функции;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; находить нужные формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами
Геометрия
уметь
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задачи; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин, в том числе тригонометрических функций; находить стороны, углы и площади треугольников, правильных многоугольников, некоторых четырехугольников, длины ломаных и дуг окружности; находить площади основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами.
Элементы логики, комбинаторики, статистики и теории вероятностей
Уметь
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждения;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятность случайного события в простейших случаях.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве в диалоге;
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности;
решения учебных и практических задач, требующих системного перебора вариантов;
сравнения шансов наступления случайных событий, для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
Способы достижения и формы оценки результатов обучения.
Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
Основными формами проверки знаний и умений, учащихся по математике являются письменная контрольная работа и устный опрос.
Оценка устных ответов учащихся.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания
Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившие математического содержания ответа, исправленные по замечанию учителя.
допущены ошибки или более двух недочетов при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»).
имелись затруднения или допущены ошибки в определении понятий и, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Оценка письменных контрольных работ учащихся.
Отметка «5» ставится в следующих случаях:
работа выполнена полностью.
в логических рассуждениях и обоснованиях нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала)
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умения обосновывать рассуждения не являлись специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки);
Отметка «3» ставится, если:
допущены более одной ошибки или более двух- трех недочетов в выкладках, чертежах или графика, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что учащийся не владеет обязательными знаниями по данной теме в полной мере.
Перечень контрольных работ
Алгебра:
Контрольная работа №1 «Свойства функций. Квадратный трёхчлен»
Контрольная работа №2 «Квадратичная и степенная функции»
Контрольная работа № 3 «Уравнения и неравенства с одной переменной»
Контрольная работа № 4 «Уравнения и неравенства с двумя переменными»
Контрольная работа №5 «Арифметическая прогрессия»;
Контрольная работа №6 «Геометрическая прогрессия»;
Контрольная работа № 7 «Элементы комбинаторики и теории вероятностей»
Контрольная работа №8 Итоговая контрольная работа, 2 ч
Геометрия:
Контрольная работа №1 «Векторы. Метод координат»
Контрольная работа № 2 «Соотношения между сторонами и углами треугольника»
Контрольная работа № 3 «Длина окружности и площадь круга»
Контрольная работа №4 «Движения»
Контрольная работа №5 Итоговая контрольная работа
Перечень учебно-методического обеспечения образовательного процесса
Учебный комплект для учащихся:
Макарычев и др. Алгебра 9. Учебник для 9 класса общеобразовательных учреждений.- М., Просвещение, 2009-2012.
Геометрия, 7 – 9: Учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2009-2012.
Методические пособия для учителя:
Программа для общеобразовательных учреждений. Математика. Министерство образования Российской Федерации.
Федеральный общеобразовательный стандарт. Вестник образования. №12,2004.
Макарычев Ю.Н. Алгебра 9. Учебник для учащихся 9 класса с углубленным изучением математики. – М., Мнемозина, 2010г.
Макарычев Ю.Н., Н.Г. Миндюк, Л.М. Короткова «Дидактические материалы по алгебре для 9 класса М., Просвещение 1996г
А.Н. Рурукин, С.А. Полякова «Поурочные разработки по алгебре 9 класс», М.: «ВАКО», 2011г.
И.В. Гришина «Математика (алгебра).9 класс. Тесты.» – Саратов: Лицей, 2011. в 2 частях.
И.М. Сугоняев «Математика. 9 класс. Тренировочные работы к экзамену. ГИА.» – Саратов: Лицей, 2011.
Алтынов П.И. Тесты. Алгебра (7-9 кл.). М.:Дрофа 2000г
Поурочные разработки по геометрии 9 класс / Н. Ф. Гаврилова. – М.: «ВАКО», 2011г.
Научно-теоретический и методический журнал «Математика в школе»
Еженедельное учебно-методическое приложение к газете «Первое сентября» Математика
CD «Уроки геометрии Кирилла и Мефодия 7-9 классы»
В.И. Жохов, Г.Д. Карташева, Л.Б. Крайнева – «Уроки геометрии в 7-9 классах», методические рекомендации для учителя к учебнику Л.С. Атанасяна, 2003г.
Г.И. Кукарцева «Сборник задач по геометрии 7-9 классы», Москва «Аквариум», 1999г.
Б.Г. Зив. Дидактические материалы по геометрии для 9 класса- М. Просвещение, 2003.
Л. С. Атанасян, В. Ф. Бутузов. Ю. А. Глазков, В. Б. Некрасов, И. И. Юдина Изучение геометрии в 7-9 классах. Методические рекомендации.- М.: Просвещение 2003 г.
Образовательные диски.
Математика 5 – 11 классы. Практикум. Под редакцией Дубровского. НФПК 2004 год.
Математика 5 – 11 классы. Практикум. Дрофа. 2004.
Лист корректировки календарно - тематического планирования
Класс
|
Дата
|
Количество
непроведен-
ных
уроков
|
Причина
|
Коррекция
|
Согласование с курирующим завучем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение:
Контрольные работы.
Алгебра
К-1
Вариант 1.
1. Дана функция 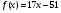 . При каких значениях аргумента . При каких значениях аргумента 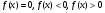 ? Является ли эта функция возрастающей или убывающей? ? Является ли эта функция возрастающей или убывающей?
2. Разложите на множители квадратный трехчлен:
а) 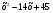 ; б) ; б) 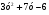 . .
3. Сократите дробь 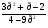 . .
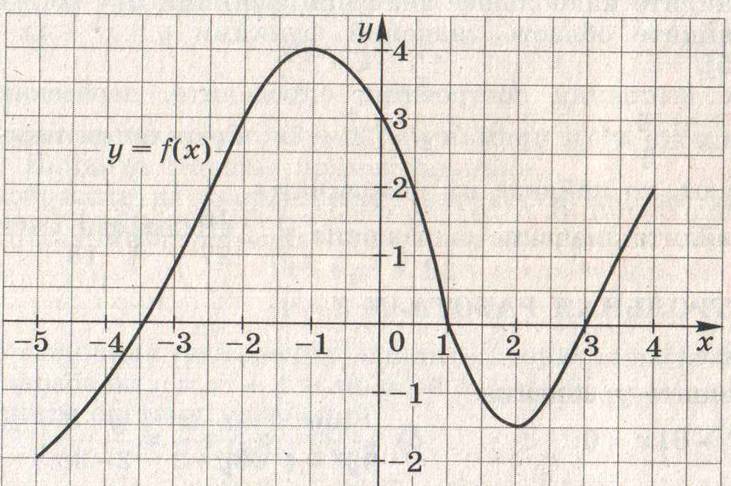
4. Область определения функции g – отрезок 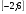 . Найдите нули функции, промежутки возрастания и убывания, область значений функции. . Найдите нули функции, промежутки возрастания и убывания, область значений функции.
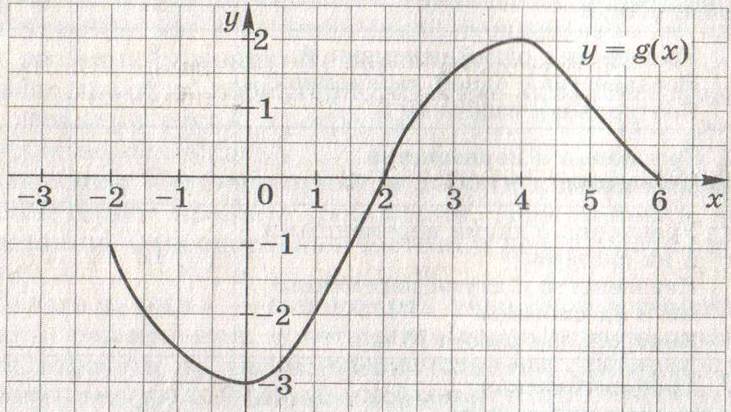
5. Сумма положительных чисел а и b равна 50. При каких значениях а и b их произведение будет наибольшим?
|
К-1
Вариант 2.
1. Дана функция 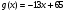 . При каких значениях аргумента . При каких значениях аргумента 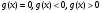 ? Является ли эта функция возрастающей или убывающей? ? Является ли эта функция возрастающей или убывающей?
2. Разложите на множители квадратный трехчлен:
а) 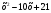 ; б) ; б) 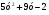 . .
3. Сократите дробь 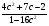 . .
4. Область определения функции f – отрезок 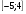 . Найдите нули функции, промежутки возрастания и убывания, область значений функции. . Найдите нули функции, промежутки возрастания и убывания, область значений функции.
5. Сумма положительных чисел с и d равна 70. При каких значениях c и d их произведение будет наибольшим?
|
К-2
Вариант 1.
1. Постройте график функции 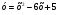 . Найдите с помощью графика: . Найдите с помощью графика:
а) значение у при х = 0,5;
б) значения х, при которых у = – 1;
в) нули функции; промежутки, в которых
y > 0 и в которых y < 0;
г) промежуток, на котором функция возрастает.
2. Найдите наименьшее значение функции 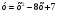 . .
3. Найдите область значений функции 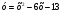 , где , где 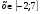 . .
4. Не выполняя построения, определите, пересекаются ли парабола 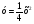 и прямая и прямая 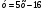 . Если точки пересечения существуют, то найдите их координаты. . Если точки пересечения существуют, то найдите их координаты.
5. Найдите значение выражения 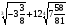
|
К-2
Вариант 2.
1. Постройте график функции 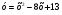 . Найдите с помощью графика: . Найдите с помощью графика:
а) значение у при х = 1,5;
б) значения х, при которых у = 2;
в) нули функции; промежутки, в которых
y > 0 и в которых y < 0;
г) промежуток, на котором функция убывает.
2. Найдите наибольшее значение функции 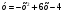 . .
3. Найдите область значений функции 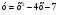 , где , где 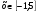 . .
4. Не выполняя построения, определите, пересекаются ли парабола 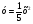 и прямая и прямая 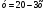 . Если точки пересечения существуют, то найдите их координаты. . Если точки пересечения существуют, то найдите их координаты.
5. Найдите значение выражения 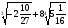
|
К-3
Вариант 1.
1. Решите уравнение:
а) 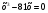 ; ;
б) 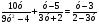 . .
2. Решите неравенство:
а) 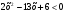 ; б) ; б) 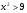 . .
3. Решите неравенство методом интервалов:
а) 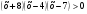 ; б) ; б) 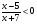 . .
4. Решите биквадратное уравнение
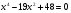 . .
5. При каких значениях т уравнение 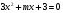 имеет два корня? имеет два корня?
6. Найдите область определения функции
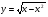 . .
7. Найдите координаты точек пересечения графиков функций 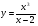 и и 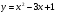 . .
|
К-3
Вариант 2.
1. Решите уравнение:
а) 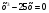 ; б) ; б) 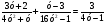 . .
2. Решите неравенство:
а) 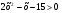 ; б) ; б) 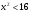 . .
3. Решите неравенство методом интервалов:
а) 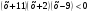 ; б) ; б) 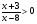 . .
4. Решите биквадратное уравнение
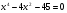 . .
5. При каких значениях п уравнение 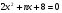 не имеет корней? не имеет корней?
6. Найдите область определения функции
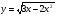 . .
7. Найдите координаты точек пересечения графиков функций 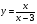 и и 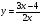 . .
|
К-4
Вариант 1.
1. Решите систему уравнений 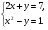
2. Периметр прямоугольника равен 28 м, а его площадь равна 40 м2. Найдите стороны прямоугольника.
3. Изобразите на координатной плоскости множество решений системы неравенств
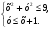
4. Не выполняя построения, найдите координаты точек пересечения параболы 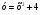 и прямой и прямой 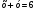 . .
5. Решите систему уравнений 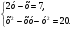
|
К-4
Вариант 2.
1. Решите систему уравнений 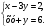
2. Одна из сторон прямоугольника на 2 см больше другой стороны. Найдите стороны прямоугольника, если его площадь равна 120см2.
3. Изобразите на координатной плоскости множество решений системы неравенств
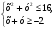
4. Не выполняя построения, найдите координаты точек пересечения окружности 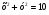 и прямой и прямой 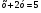 . .
5. Решите систему уравнений 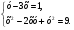
|
К-5
Вариант 1.
1. Найдите двадцать третий член арифметической прогрессии 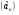 , если , если 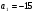 и и 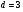 . .
2. Найдите сумму шестнадцати первых членов арифметической прогрессии: 8; 4; 0; … .
3. Найдите сумму шестидесяти первых членов последовательности 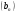 , заданной формулой , заданной формулой 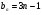 . .
4. Является ли число 54,5 членом арифметической прогрессии 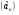 , в которой , в которой 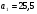 и и 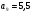 ? ?
5. Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 100.
|
К-5
Вариант 2.
1. Найдите восемнадцатый член арифметической прогрессии 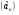 , если , если 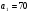 и и 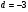 . .
2. Найдите сумму двадцати первых членов арифметической прогрессии: – 21; – 18; – 15; … .
3. Найдите сумму сорока первых членов последовательности 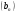 , заданной формулой , заданной формулой 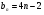 . .
4. Является ли число 30,4 членом арифметической прогрессии 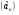 , в которой , в которой 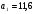 и и 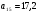 ? ?
5. Найдите сумму всех натуральных чисел, кратных 7 и не превосходящих 150.
|
К-6
Вариант 1.
1. Найдите седьмой член геометрической прогрессии 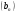 , если , если 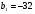 и и 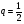 . .
2. Первый член геометрической прогрессии 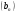 равен 2, а знаменатель равен 3. Найдите сумму шести первых членов этой прогрессии. равен 2, а знаменатель равен 3. Найдите сумму шести первых членов этой прогрессии.
3. Найдите сумму бесконечной геометрической прогрессии: 24; –12; 6; … .
4. Найдите сумму девяти первых членов геометрической прогрессии 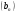 с положительными членами, зная, что с положительными членами, зная, что 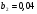 и и 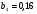 . .
|
К-6
Вариант 2.
1. Найдите шестой член геометрической прогрессии 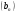 , если , если 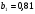 и и 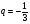 . .
2. Первый член геометрической прогрессии 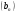 равен 6, а знаменатель равен 2. Найдите сумму семи первых членов этой прогрессии. равен 6, а знаменатель равен 2. Найдите сумму семи первых членов этой прогрессии.
3. Найдите сумму бесконечной геометрической прогрессии: – 40; 20; – 10; … .
4. Найдите сумму восьми первых членов геометрической прогрессии 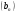 с положительными членами, зная, что с положительными членами, зная, что 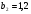 и и 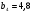 . .
|
К-7
Вариант 1.
1. Сколькими способами могут разместиться 5 человек в салоне автобуса на 5 свободных местах?
2. Сколько трехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 1, 2, 5, 7, 9?
3. Победителю конкурса книголюбов разрешается выбрать две книги из 10 различных книг. Сколькими способами он может осуществить этот выбор?
4. В доме 90 квартир, которые распределяются по жребию. Какова вероятность того, что жильцу не достанется квартира на первом этаже, если таких квартир 6?
5. Из 8 мальчиков и 5 девочек надо выделить для работы на пришкольном участке 3 мальчиков и 2 девочек. Сколькими способами это можно сделать?
6. На четырех карточках записаны цифры 1, 3, 5, 7. Карточки перевернули и перемешали. Затем наугад последовательно положили эти карточки в ряд одну за другой и открыли. Какова вероятность того, что в результате получится число 3157?
|
К-7
Вариант 2.
1. Сколько шестизначных чисел можно составить из цифр 1, 2, 3, 5, 7, 9 без повторений цифр?
2. Из 8 учащихся класса, успешно выступивших на школьной олимпиаде, надо выбрать двух для участия в городской олимпиаде. Сколькими способами можно сделать этот выбор?
3. Из 15 туристов надо выбрать дежурного и его помощника. Какими способами это можно сделать?
4. Из 30 книг, стоящих на полке, 5 учебников, а остальные художественные произведения. Наугад берут с полки одну книгу. Какова вероятность того, что она не окажется учебником?
5. Из 9 книг и 6 журналов надо выбрать 2 книги и 3 журнала. Сколькими способами можно сделать этот выбор?
6. На пяти карточках написаны буквы а, в, и, л, с. Карточки перевернули и перемешали. Затем наугад последовательно положили эти карточки в ряд одну за другой и открыли. Какова вероятность того, что в результате получится слово «слива»?
|
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА
Вариант 1.
1. Упростите выражение 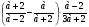 . .
2. Решите систему уравнений 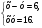
3. Решите неравенство 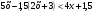 . .
4. Представьте выражение 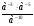 в виде степени с основанием а. в виде степени с основанием а.
5. Постройте график функции 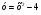 . Укажите, при каких значениях х функция принимает положительные значения. . Укажите, при каких значениях х функция принимает положительные значения.
6. В фермерском хозяйстве под гречиху было отведено два участка. С первого участка собрали 105 ц гречихи, а со второго, площадь которого на 3 га больше, собрали 152 ц. Найдите площадь каждого участка, если известно, что урожайность гречихи на первом участке была на 2 ц с 1 га больше, чем на втором.
|
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА
Вариант 2.
1. Упростите выражение 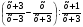 . .
2. Решите систему уравнений 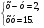
3. Решите неравенство 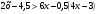 . .
4. Представьте выражение 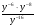 в виде степени с основанием у. в виде степени с основанием у.
5. Постройте график функции 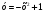 . Укажите, при каких значениях х функция принимает отрицательные значения. . Укажите, при каких значениях х функция принимает отрицательные значения.
6. Из пункта А в пункт В, расстояние между которыми 45 км, выехал велосипедист. Через 30 мин вслед за ним выехал второй велосипедист, который прибыл в пункт В на 15 мин раньше первого. Какова скорость первого велосипедиста, если она на 3 км/ч меньше скорости второго?
| |
|
|
 Скачать 0.54 Mb.
Скачать 0.54 Mb.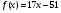 . При каких значениях аргумента
. При каких значениях аргумента 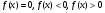 ? Является ли эта функция возрастающей или убывающей?
? Является ли эта функция возрастающей или убывающей?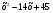 ; б)
; б) 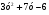 .
. 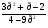 .
.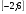 . Найдите нули функции, промежутки возрастания и убывания, область значений функции.
. Найдите нули функции, промежутки возрастания и убывания, область значений функции.
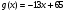 . При каких значениях аргумента
. При каких значениях аргумента 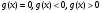 ? Является ли эта функция возрастающей или убывающей?
? Является ли эта функция возрастающей или убывающей?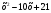 ; б)
; б) 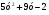 .
. 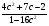 .
.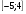 . Найдите нули функции, промежутки возрастания и убывания, область значений функции.
. Найдите нули функции, промежутки возрастания и убывания, область значений функции.
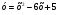 . Найдите с помощью графика:
. Найдите с помощью графика: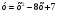 .
. 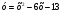 , где
, где 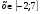 .
.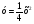 и прямая
и прямая 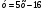 . Если точки пересечения существуют, то найдите их координаты.
. Если точки пересечения существуют, то найдите их координаты.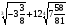
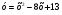 . Найдите с помощью графика:
. Найдите с помощью графика: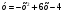 .
. 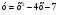 , где
, где 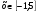 .
.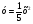 и прямая
и прямая 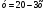 . Если точки пересечения существуют, то найдите их координаты.
. Если точки пересечения существуют, то найдите их координаты.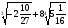
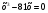 ;
; 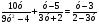 .
.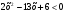 ; б)
; б) 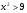 .
. 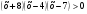 ; б)
; б) 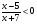 .
.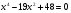 .
.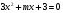 имеет два корня?
имеет два корня?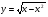 .
.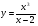 и
и 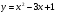 .
.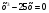 ; б)
; б) 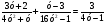 .
.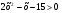 ; б)
; б) 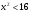 .
. 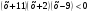 ; б)
; б) 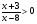 .
.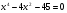 .
.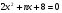 не имеет корней?
не имеет корней?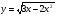 .
.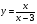 и
и 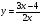 .
.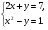
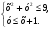
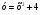 и прямой
и прямой 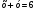 .
.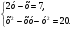
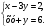
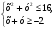
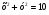 и прямой
и прямой 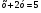 .
.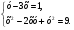
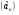 , если
, если 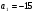 и
и 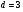 .
.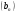 , заданной формулой
, заданной формулой 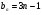 .
.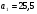 и
и 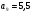 ?
?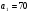 и
и 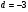 .
.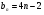 .
.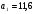 и
и 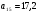 ?
?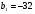 и
и 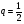 .
.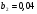 и
и 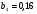 .
.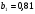 и
и 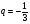 .
.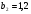 и
и 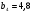 .
.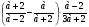 .
.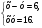
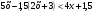 .
.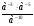 в виде степени с основанием а.
в виде степени с основанием а.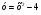 . Укажите, при каких значениях х функция принимает положительные значения.
. Укажите, при каких значениях х функция принимает положительные значения.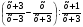 .
.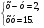
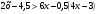 .
.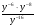 в виде степени с основанием у.
в виде степени с основанием у.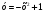 . Укажите, при каких значениях х функция принимает отрицательные значения.
. Укажите, при каких значениях х функция принимает отрицательные значения.