Рабочая программа по алгебре для 9 общеобразовательных классов Учитель Ф. Попондополо
 Скачать 277.5 Kb. Скачать 277.5 Kb.
|
| Бюджетное государственное общеобразовательное учреждение Средняя общеобразовательная школа № 354 Московского района Санкт-Петербурга Согласовано Зам. директора по УВР ___________ Е.Л.Кот «____» августа 2012 г. Утверждаю Директор СОШ № 354 Санкт-Петербурга _________Л.А.Шнырикова «___» августа 2012 г. Рассмотрено на методическом объединении СОШ № 354 Протокол №__ от ___.08.2012 Руководитель МО ___________ РАБОЧАЯ ПРОГРАММА по алгебре для 9 общеобразовательных классов Учитель Ф. Попондополо И. Наталья О. Юрьевна Санкт-Петербург 2012 Пояснительная записка Рабочая программа учебного предмета алгебра для 9 класса составлена на основе Примерной программы по учебным предметам. Математика 5-9 классы. — М.: Просвещение, 2011. (Стандарты второго поколения) и авторской программы Ш.А.Алимова, Ю.М.Колягина, Ю.В.Сидорова. Примерная программа основного общего образования по математике составлена на основе Фундаментального ядра содержания общего образования и Требований к результатам общего образования, представленных в федеральном государственном образовательном стандарте общего образования, с учетом преемственности с Примерными программами для начального общего образования. В ней также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования. Цели обучения математике в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека. Алгебра нацелена на формирование математического аппарата для решения задач из математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др.). Школьное математическое образование ставит следующие цели обучения:
В задачи обучения математики входит: Овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования; Овладение навыками дедуктивных рассуждений; Интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, необходимой, в частности, для освоения курса информатики; Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов; Получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и т.д.); Воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса; Развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами. Требования к результатам обучения и освоению содержания курса Изучение математики в основной школе дает возможность обучающимся достичь следующих результатов развития: В личностном направлении:
В метапредметном направлении: 1) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов; 2) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни; 3) умение находить в различных источниках информацию, необходимую для решения математических проблем, и пред-ставлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации; 4) умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) Для иллюстрации, интерпретации, аргументации; 5) умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; 6) умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач; 7) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; 8) умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем; 9) умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера; В предметном направлении: 1) овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления; 2) умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений; 3) развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками устных, письменных, инструментальных вычислений; 4) овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем; умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса; 5) овладение системой функциональных понятий, функциональным языком и символикой; умение использовать функционально-графические представления для описания и анализа реальных зависимостей; 6) овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях; 7) овладение геометрическим языком, умение использовать его для описания предметов окружающего мира; развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений; 8) усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне — о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач; 9) умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов геометрических фигур; 10) умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера. Курс алгебры построен в соответствии с традиционными содержательно-методическими линиями: числовой, функциональной, алгоритмической, уравнений и неравенств, алгебраических преобразований. В курсе алгебры 9-го класса продолжается систематизация и расширение сведений о функциях. На этапе 9-го класса завершается изучение рациональных уравнений с одной переменной. Дается понятие целого рационального уравнения и его степени. Особое внимание уделяется решению уравнений третьей и четвертой степени с помощью разложения на множители и введения вспомогательной переменной, что широко используется в дальнейшем при решении тригонометрических, логарифмических и других видов уравнений. Рассматриваются системы, содержащие уравнения второй степени с двумя неизвестными. Даются первые знания об арифметической и геометрической прогрессиях, как о частных видах последовательностей. Изучая формулу нахождения суммы первых членов арифметической прогрессии и формулу суммы первых членов геометрической прогрессии , целесообразно уделить внимание заданиям, связанным с непосредственным применением этих формул. Из курса геометрии продолжается изучение синуса, косинуса и тангенса острого угла прямоугольного треугольника. Вводится понятие котангенса угла. Изучаются свойства синуса, косинуса, тангенса и котангенса, которые находят применение в преобразованиях тригонометрических выражений. Специальное внимание уделяется переходу от радианной меры угла к градусной мере и наоборот. Центральное место занимают формулы, выражающие соотношения между тригонометрическими функциями одного и того же аргумента. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов. Программой отводится на изучение алгебры по 3 урока в неделю, что составляет 105 часов в учебный год. В рабочей программе предусмотрено 8 контрольных работ. Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов. Количество часов по темам изменено в связи со сложностью тем. Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных работ и математических диктантов (по 10 - 15 минут) в конце логически законченных блоков учебного материала. Итоговая аттестация предусмотрена в виде административной контрольной работы. При организации учебного процесса будет обеспечена последовательность изучения учебного материала: новые знания опираются на недавно пройденный материал; обеспечено поэтапное раскрытие тем с последующей реализацией; закрепление в процессе практикумов и деловых игр тренингов и итоговых собеседований; будут использоваться уроки-соревнования, уроки консультации, зачёты Основные типы учебных занятий:
Основным типом урока является комбинированный. При изучении курса проводится 2 вида контроля: Текущий – контроль в процессе изучения темы; Формы: устный опрос, тестирование, самостоятельные работы Итоговый – контроль в конце изучения зачетного раздела; Формы: устные и письменные зачетные работы по отдельным темам, собеседование, практические работы. В каждом разделе уделяется внимание привитию навыков самостоятельной работы. В ходе изучения материала планируется проведение 7 контрольных работ по основным темам и 1 итоговой контрольной работы. Требования к уровню подготовки учащихся 9 классов (базовый уровень): Должны знать: значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
Должны уметь: выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
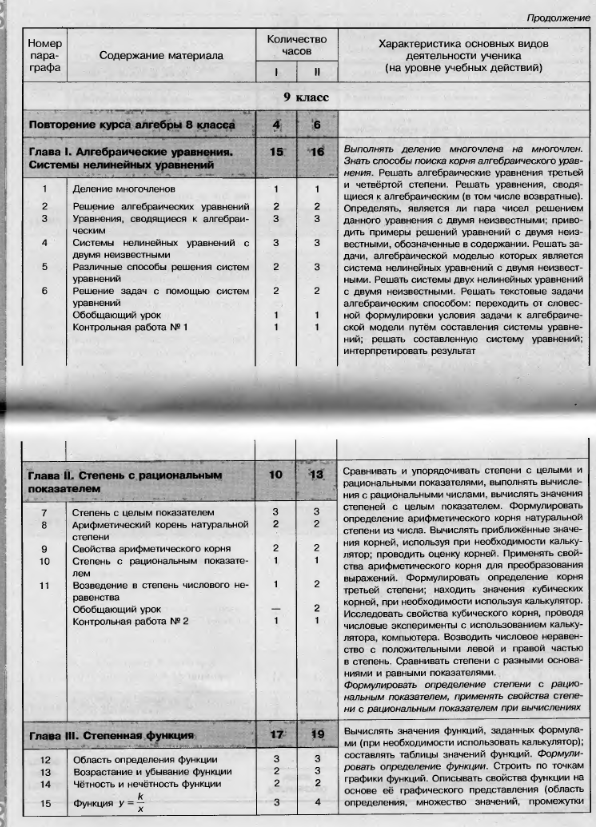
Владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной. Способны решать следующие жизненно-практические задачи: Самостоятельно приобретать и применять знания в различных ситуациях, работать в группах, аргументировать и отстаивать свою точку зрения, уметь слушать других, извлекать учебную информацию на основе сопоставительного анализа объектов, пользоваться предметным указателем энциклопедий и справочников для нахождения информации, самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем. Содержание обучения 1.Вводное повторение – 4 часа. Квадратные уравнения, замена переменной, биквадратное уравнение. Неравенства второй степени с одной переменной, нули функции, метод интервалов, график квадратичной функции. Уметь выполнять упражнения из разделов курса VIII класса: решать квадратные уравнения и неравенства, задачи с помощью квадратных уравнений, строить график квадратичной функции. Знать формулы решения квадратных уравнений, алгоритм построения параболы, теорему Виета. 2. Алгебраические уравнения. Системы нелинейных уравнений – 14 часов. Знать: алгоритм решения алгебраических уравнений и уравнений, сводящихся к ним. Уметь: решать алгебраические уравнения и системы уравнений, выполнять деление многочленов, решать задачи с помощью уравнений. .Основные термины по разделу: Многочлен, алгоритм деления многочленов, формула деления многочленов, уравнения третьей и четвёртой степеней, понятие возвратного уравнения, системы нелинейных уравнений. 3. Степень с рациональным показателем – 12 часов. Знать: степень с целым и рациональным показателями и их свойства; степень с нулевым и отрицательным показателями; определение арифметического корня натуральной степени и его свойства. Уметь: находить значение степени с целым показателем при конкретных значениях основания и показателя степени и применять свойства степени для вычисления значений числовых выражений и выполнения простейших преобразований. Основные термины по разделу: Определение степени с целым отрицательным и рациональным показателем; нулевым показателем, определение и свойства арифметического корня n-й степени. 4. Степенная функция – 16 часов. Знать: понятия область определения, чётность и нечётность функции, возрастание и убывание функции на промежутке. Уметь: строить графики линейных и дробно-линейных функций и по графику перечислять их свойства; решать уравнения и неравенства, содержащие степень. Основные термины по разделу: Функция, область определения и область изменения, нули функции, возрастающая и убывающая функция, четные и нечетные функции, их симметричность, понятие функции у=k/х, обратно пропорциональная зависимость, свойства степенной функции, иррациональное уравнение. 5. . Прогрессии – 14 часов. Знать: определения арифметической и геометрической прогрессий, формулы суммы n первых членов арифметической и геометрической прогрессий; определение бесконечно убывающей геометрической прогрессии. Уметь: решать задачи на нахождение неизвестного члена арифметической и геометрической прогрессии, проверять является ли данное число членом прогрессии, находить сумму n первых членов прогрессии. Основные термины по разделу: Арифметическая и геометрическая прогрессии, формула n-го члена прогрессии, формула суммы n-членов прогрессии. И нескольких первых членов прогрессий. 6 Случайные события – 11 часов. Уметь: ориентироваться в комбинаторике; строить дерево возможных вариантов Знать и уметь пользоваться формулами для решения комбинаторных задач Основные термины по разделу: Перебор возможных вариантов, комбинаторное правило умножения, перестановки, число всевозможных перестановок, размещения, сочетания. 7. Случайные величины – 11 часов. Уметь: определять количество равновозможных исходов некоторого испытания; Знать классическое определение вероятности, формулу вычисления вероятности в случае исхода противоположных событий Основные термины по разделу: Случайное событие, относительная частота, классическое определение вероятности, противоположные события, независимые события, несовместные и совместные события. 8. Множества. Логика – 10 часов. Уметь: решать задачи, применяя теоремы множеств, круги Эйлера, с использованием логических связок «и», «или», «не». Знать понятия множества, подмножества, пересечение множеств, объединение множеств; понятие высказывания. Основные термины по разделу: Множество, подмножество, высказывание, логическая связка. 9. Итоговое повторение - 13 часов. -знать алгоритм построения графика функции; формулы n-го члена и суммы n членов арифметической и геометрической прогрессий и уметь их применять при решении задач -уметь строить графики функции; по графику определять свойства функции -уметь решать уравнения третьей и четвертой степени с одним неизвестным с помощью разложения на множители и введения вспомогательной переменной; решать неравенства методом интервалов; решать системы уравнений; решать задачи с помощью составления систем. Данная программа содержит все темы , включенные в федеральный компонент содержания образования. Содержание программы носит локальный (созданный для данного образовательного учреждения) и индивидуальный (разработанный учителем ) характер Содержание курса алгебры 9 класса включает следующие тематические блоки:
Список используемой литературы: 1. Учебник для учащихся 9 класса общеобразовательных учреждений под редакцией коллектива, авторов: Ш.А.Алимова, Ю.М.Колягина, Ю.В.Сидорова .Алгебра. 9 класс .-М.:Просвещение , 2010. 2. Методическое пособие к учебнику Алимова. 9 класс. 3. Программа для общеобразовательных учреждений: алгебра для 5-9 классов, составитель Т.А. Бурмистрова, издательство просвещение, 2011 г., 4. Стандарт основного общего образования по математике. 5. В.И. Жохов. «Дидактические материалы по алгебре. 9 класс» 5. Л.В.Кузнецова «Сборник заданий для подготовки к итоговой аттестации в 9 классе».-М.,: Просвещение, 2006. 6. Ткачева М.В., Федорова Н.Е. «Элементы статистики и вероятность». М.,: Просвещение, 2007 7.Интернет портал proшколу.ru https://proshkolu.ru/ 8.https://school-collection.edu.ru/ – единая коллекция цифровых образовательных ресурсов.
    Требования к математической подготовке Уметь выполнять действия с обыкновенными и десятичными дробями. Уметь выполнять тождественные преобразования алгебраических выражений. Знать формулы сокращенного умножения. Уметь решать линейные и квадратные уравнения и неравенства и их системы. Знать понятие функции, свойства функций. Уметь решать квадратные, рациональные уравнения, сводящиеся к ним. Уметь решать системы двух линейных уравнений и несложные нелинейные системы. Уметь решать текстовые задачи алгебраическим методом. Знать как используются уравнения и системы уравнений на практике. Знать понятие функции, свойства функций. Уметь выполнять основные действия со степенями с целыми показателями. Уметь применять свойства арифметических корней для вычислений значений и преобразований числовых выражений, содержащих арифметические корни. Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами. Знать, как математически степенные функции могут описывать реальные зависимости; приводить примеры такого описания и уметь применить это при решении практических задач. Уметь находить значения функции, заданной формулой, таблицей, графиком по ее аргументу. Уметь находить значение аргумента по значению функции, заданной графиком или таблицей. Уметь определять свойства степенной функции по ее графику. Уметь описывать свойства степенных функций, строить их графики. Уметь применять графические представления при решении уравнений, неравенств и систем. Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для интерпретации графиков реальных зависимостей между величинами. Распознавать арифметические и геометрические прогрессии. Решать задачи с применением формул общего члена и нескольких первых членов прогрессий. Уметь решать несложные комбинаторные задачи Уметь решать комбинаторные задачи с использованием правила умножения; Уметь находить вероятности случайных событий в простейших случаях. Уметь находить частоту события, используя собственные наблюдения и готовые статистические данные. Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения учебных и практических задач, требующих систематического перебора вариантов. Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||