|
1. Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
Уровневые контрольные работы оцениваются:
«3» - выполнено задание репродуктивного уровня;
«4» - выполнено задание репродуктивного уровня + задание конструктивного уровня;
«5» - выполнено задание репродуктивного уровня + задание конструктивного уровня + задание творческого уровня.
Тестовые работы оцениваются по критериям данного теста.
Тематический план курса алгебры и начал анализа 11 класс.
№
|
Содержание
|
Кол-во часов
|
Кол-во к.р.
|
1.
|
Повторение курса за 10 класс
|
5
|
к.р. вход
|
Глава III. Первообразная и интеграл
|
18
|
|
2
|
Первообразная.
|
9
|
к.р. №1
|
3.
|
Интеграл
|
9
|
к.р. №2
|
Глава IV. Показательная и логарифмическая функции
|
38
|
|
4.
|
Обобщение понятие степени
|
10
|
к.р. №3
|
5.
|
Показательная и логарифмическая функции
|
16
|
к.р. №4
|
6.
|
Производная показательной и логарифмической функций
|
12
|
к.р. № 5
|
Глава V. Задачи на повторение
|
41
|
|
7.
|
Действительные числа
|
6
|
|
8.
|
Тождественные преобразования
|
8
|
|
9.
|
Функции
|
6
|
|
10.
|
Уравнения, неравенства, системы уравнений и неравенств
|
14
|
к.р. №6
|
11.
|
Производная
|
5
|
|
12.
|
Репетиционный экзамен
|
1
|
Итоговая к.р.
|
13.
|
Обобщение курса
|
1
|
|
14.
|
Резерв
|
3
|
|
|
Всего
|
105
|
8
|
Основное содержание
Алгебра и начала анализа (102часов)
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Первообразная. Понятие об определенном интеграле как площади криволинейной трапеции. Формула Ньютона-Лейбница. Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Примеры применения интеграла в физике и геометрии. Вторая производная и ее физический смысл.
АЛГЕБРА
Корни и степени. Корень степени n>1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Логарифм. Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е. Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования.
ФУНКЦИИ.
Показательная функция (экспонента), её свойства и график. Логарифмическая функция, её свойства и график. Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой 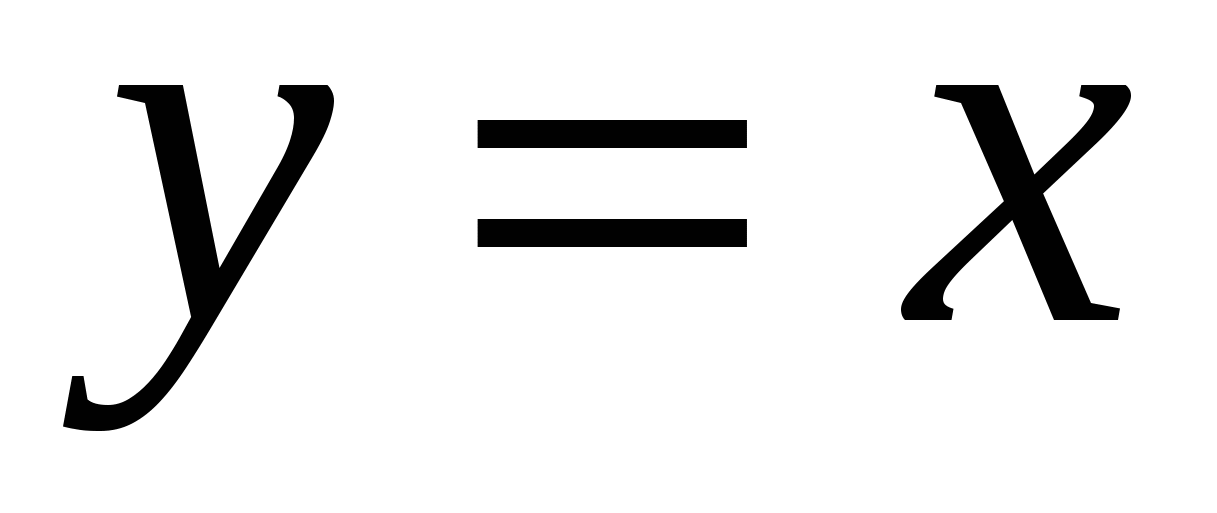 , растяжение и сжатие вдоль осей координат. , растяжение и сжатие вдоль осей координат.
УРАВНЕНИЯ И НЕРАВЕНСТВА
Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных и тригонометрических уравнений.
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенства с двумя переменными и их систем. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
РЕШЕНИЕ ТИПОВЫХ ТЕСТОВЫХ ЗАДАНИЙ
Формирование представлений о различных типах тестовых заданий, которые включаются в ЕГЭ по математике. Овладение навыкам и умениями решения заданий разного уровня: тестовых заданий с выбором ответа, качественных заданий с числовым ответом, заданий повышенного уровня с полным ответом. Развитие творческих способностей применения знаний и умений в решении вариантов ЕГЭ по математике.
Календарно-тематическое планирование алгебры и начал анализа, 11 класс
№ уро
ка
|
Тема урока
|
Кол-во часов/пункт
|
Тип урока
|
Вид контроля, измерители
|
Элементы содержания урока
|
Требования к уровню подготовки
|
Дополнительные знания. Умения требования повышеного уровня
|
Д/З
|
сроки изучения
|
план
|
факт
|
Повторение курса за 10 класс (5 часов)
Цель:
- формирование представлений о целостности и непрерывности курса алгебры 10 класса;
- овладение умениями обобщения и систематизации знаний учащихся по основным темам;
- развитие логического, математического мышления и интуиции, творческих способностей в области математики.
|
|
|
1
|
Производная функции
|
1
|
Обобщение и систематизация
|
Фронтальный опрос, ответы на вопросы по теории, упражнения
|
Формулы дифферен- цирования. Правила дифференцирования
Возрастающая и убывающая функции. Монотонность, точки экстремума Алгоритм исследования функции.
Решение методом интервалов.
|
Уметь:
-находить производные элементарных функций. произв. суммы, произвед, частного, сложной функции;
-работать с учебником. Отбирать и конструировать материал
|
Умение вывести формулы производных;
вычислять скорость изменения функции; передавать информацию кратко, сжато, полно, выборочно
|
Поиск инфор в разл источниках
|
04.09
|
|
2
|
Применение производной
|
1
|
Обобщение и систематизация
|
Фронтальный, индивидуальный опрос, построение алгоритма действий
|
Уметь:
-исследовать в простейших случаях ф-ю на монотонность, строить графики;
-объяснять изученные положения на конкретных примерах
|
Умение использовать производную при решении уравнений и неравенств. Нахождение наибольшего и наименьшего значений. Приводить примеры, подбирать аргументы, формулировать вывод
|
Конспекты уч-ся
|
05.09
|
|
|
Тригонометрические уравнения
|
1
|
Обобщение и систематизация
|
ответы на вопросы по теории, упражнения
|
Однородные тригонометрические уравнения 1 и 2 степени, метод разложения на множители. Алгоритм решения
|
Уметь:
- преобразовывать простые тригонометр выражения; решать простые тригонометрические уравнения;
- собирать материал для сообщения по теме
|
Преобразовывать сложные тригонометрические выражения; решать сложные уравнения. Вычислять значения выраж, содержащих обратные тригоном етрические функции
|
Дифференц задания
|
07.09
|
|
3
|
1
|
8.09
|
|
5
|
Входная контрольная работа
|
1
|
Контроль обобщение и коррекция
|
Решение контрольных заданий
|
Проверить умения и навыки по повторению материала за 10 класс
|
Уметь:
- обобщать и систематизировать знания по основным темам курса 10 класса; развернуто обосновывать решения
|
Уметь обобщать и систематизировать знания на сложных примерах. Владеть навыками самоконт роля и самоанализа
|
Создание базы тестовых заданий
|
09.09
|
| |
|
|
 Скачать 0.79 Mb.
Скачать 0.79 Mb.