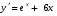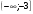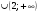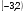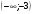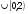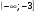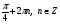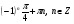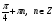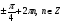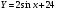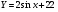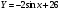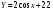Протокол № от Председатель мк / / Утверждаю Директор гбоу спо рпт мо
 Скачать 148.88 Kb. Скачать 148.88 Kb.
|
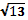 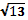 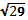 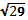 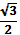 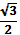 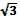 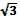 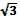 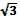 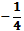 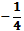 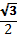 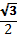 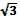 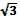 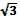  Государственное бюджетное образовательное учреждение Государственное бюджетное образовательное учреждениесреднего профессионального образования «Раменский политехнический техникум» МО
Программа итогового экзамена ПД.01 Математика Раменское 2014 г. Пояснительная записка Программа итогового экзамена по математике предназначена для студентов ГБОУ СПО «Раменский политехнический техникум» МО. Основной формой проверки знаний за курс математики является тест. На выполнение экзаменационной работы по математике дается 4 часа (240 мин). Работа состоит из двух частей и содержит 21 задание. Программа итогового экзамена по математике Для успешной подготовки к итоговому экзамену по математике в 2014 году студентам ГБОУ СПО «Раменский политехнический техникум» МО следует обратить особое внимание на повторение тем, согласно стандарта.
Основные формулы тригонометрии. Функции и их графики. Решение тригонометрических уравнений и неравенств.
Правила вычисления производных. Производная сложной функции. Производная показательной функции. Метод интервалов. Применение производной к исследованию функции. Применение производной в физике.
Основное свойство первообразной. Правила нахождения первообразных.
Корень n-ой степени и его свойства. Степень с рациональным показателем. Решение иррациональных уравнений. 5. Показательная и логарифмическая функции: Показательная функция. Решение показательных уравнений и неравенств. Логарифмы и их свойства. Логарифмическая функция. Решение логарифмических уравнений и неравенств. Свойства функций. 6. Интеграл: Площадь криволинейной трапеции. 7. Стереометрия: Многогранники. Тела вращения. 8. Планиметрия: Соотношения между сторонами и углами в прямоугольном треугольнике. Рекомендации для проверки (проведения) экзаменационного теста. Тест состоит из 21задания. Часть 1 содержит 16 заданий. К каждому из заданий дано 4 варианта ответа, из которых только один верный. При выполнении задания в «бланке ответов» надо указать номер выбранного ответа. Часть 2 содержит 5 более сложных заданий. При их выполнении в «бланке ответов» надо записать только полученный ответ. Задания части 2 считаются выполненными, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби. При их выполнении надо записать полное решение на чистом листе и приложить к бланку ответов. Критерии оценки контрольной работы. Часть 1 задания с 1 – 16 оцениваются по 1 баллу. Часть 2 задания с 1 – 5 оцениваются по 2 балла. Максимальный балл за тест – 26. 0 – 12 баллов - «2» («неудовлетворительно») 13 – 16 баллов - «3» («удовлетворительно») 17 – 22 баллов - «4» («хорошо») 23 – 26 баллов - «5» («отлично») Бланк ответов экзаменационного теста по математике Ф.И.О.___________________________________________ Группа № _____________________ Специальность ____________________ __ вариант. Таблица 1Ответы к заданиям с выбором ответа часть 1
Таблица 2Ответы к заданиям с кратким ответом часть 2
Тестовый балл_______________ Отметка_______________ Председатель экз.ком.______________ Преподаватель__________________ Ассистент________________________ 1 вариант ЧАСТЬ 1
1. Найдите значение выражения 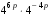 при при 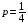 . .
2. Упростите выражение 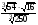 . .
3. Найдите значение выражения 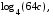 если если 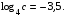
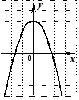
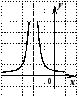
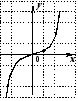
4. На одном из следующих рисунков изображен график нечетной функции. Укажите этот рисунок.
5. Найдите производную функции 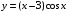 . .
6. Укажите промежуток, содержащий корень уравнения 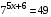 . .
7. Решите неравенство 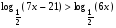 . .
8. Решите уравнение 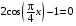 . .
9. В правильной четырехугольной пирамиде SABCD точка O- центр основания, S – вершина, SC = 73, AC = 110. Найдите длину отрезка SO. 1) 48 2) 52 3) 49 4) 47 10. Двое решают , как им обойдется дешевле доехать из Москвы в Санкт- Петербург – на поезде или автомобиле. Билет на поезд стоит 630 рублей на одного человека. Автомобиль расходует 11 литров бензина на 100 км пути, расстояние по шоссе равно 700 км, а цена бензина равна 19,5 рублям за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на двоих? 1) 1360 2) 1260 3) 1501 4) 1275 11. В треугольнике АВС угол С = 90°, угол А = 30°, АВ = . Найдите АС. 1) 1 2) 3) 1,5 4) 12. Решите уравнение 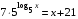 . .1) 3 2) 14 3) 2,6 4) 3,5 13. Найдите значение выражения 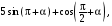 если если 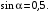 1) - 3 2) 3 3) 1 4) – 1 14. Укажите множество решений неравенства  . .
15. Вычислите значение производной функции у = sin x – 2х в точке х0 = 0. 1) 1 2) 0 3) - 3 4) - 1 16. Укажите первообразную функции 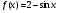 . .
1 вар. ЧАСТЬ 2
1. Решите уравнение 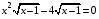 . . (Если уравнение имеет более одного корня, то в ответе запишите сумму всех его корней). 2. Найдите значение выражения 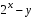 , если , если 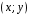 является является решением системы уравнений 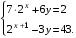 3. Найдите площадь фигуры, ограниченной линиями 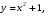 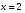 , , 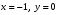 4. Шар объемом 6 м3 вписан в цилиндр. Найдите объем цилиндра (в м3). 5. Найдите наибольшее значение функции f(x) = - x3 + 12x – 14 на отрезке [- 2; 3]. Ответы к заданиям по математике для 1 варианта. Таблица 1 Ответы к заданиям с выбором ответа части 1
Таблица 2 Ответы к заданиям с кратким ответом части 2
2 вариант ЧАСТЬ 1
1. Вычислите: 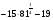 . .
2. Упростите выражение 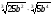 . .
3. Найдите значение выражения 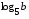 , если , если 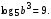
4. Решите уравнение 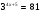 . .1) 2) 4 3) 4) - 4 5. Решите неравенство 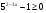 . .
6. Найдите производную функции 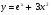 . .
7. Поезд Санкт-Петербург – Нижний Новгород отправляется в 17.30, а прибывает в 8.30 следующего дня ( время московское ). Сколько часов поезд находился в пути? 1) 13 2) 15 3) 17 4) 11 8. Упростите выражение 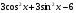 . .
9. Найдите значение выражения 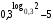 . .
10. Укажите график функции, заданной формулой 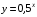 . 2 вар. . 2 вар.1) 0 y 1 x 1 2) 0 y 1 x 1 4) x 1 1 y 0 3) x 1 1 y 0 11. Решите неравенство 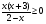 . .
12. Решите уравнение 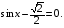
13. В треугольнике АВС угол С = 90°, угол А = 60°, ВС = . Найдите АС. 1) 2) 3) 1 4) 14. Какому промежутку принадлежит корень уравнения 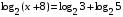 ? ?
15. Для функции 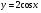 найдите первообразную, график которой проходит через точку М0 найдите первообразную, график которой проходит через точку М0  . .
16. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1 = , BB1 = 3, A1D1 = 4. Найдите длину ребра AB. 1) 2 2) 4 3) 4) 5 2 вар. ЧАСТЬ 2
1. Пусть (х0; у0) - решение системы 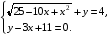 Найдите произведение 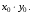 2. Точка движется по координатной прямой согласно закону 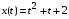 , где , где 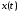 – координата точки в момент времени t. В какой момент времени скорость точки будет равна 5? – координата точки в момент времени t. В какой момент времени скорость точки будет равна 5?3. Вычислите площадь фигуры, ограниченной линиями 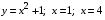 и и 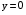 . .4. Шар объемом 8 м3 вписан в цилиндр. Найдите объем цилиндра ( в м3). 5. Найдите наименьшее значение функции f(x)=x3 - 3x2 - 9x + 31 на отрезке [-1;4] Ответы к заданиям по математике для 2 варианта. Таблица 1Ответы к заданиям с выбором ответа часть 1
Таблица 2 Ответы к заданиям с кратким ответом часть 2
|
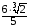
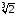
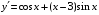
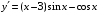
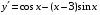
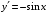
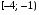
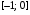
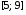
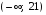
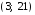
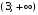
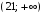
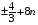 ,
, 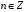
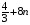 ,
, 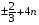 ,
, 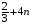 ,
, 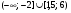
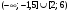
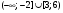
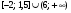
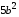
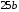
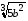
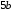
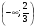
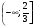
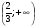
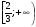
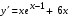 3)
3) 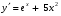
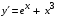 4)
4)