Протокол № от от мбоу «сош №3» Председатель мс директор мбоу «сош №3»

Название	Протокол № от от мбоу «сош №3» Председатель мс директор мбоу «сош №3»
страница	2/5
Дата	13.02.2016
Размер	0.67 Mb.
Тип	Протокол

1 2 3 4 5

3. Числовые функции (25ч)

Определение числовой функции. Независимая переменная. Зависимая переменная. Область определения функции. Область значений функции.

Способы задания функций (аналитический, графический, табличный, словесный).

Свойства функций (монотонность, ограниченность, выпуклость, наибольшее и наименьшее значения, непрерывность). . Четные и нечетные функции. Графики четной и нечетной функции.

Степенные функции с натуральным показателем, её свойства и график. Степенная функция с отрицательным целым показателем, её свойства и график. Функции y = xⁿ , (nN), их свойства и графики. Функции y = x^–ⁿ , (nN), их свойства и графики. Функция у=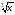

, ее свойства и график.

Основная цель — расширить сведения о свойствах функций, ознакомить учащихся со свойствами и графиком квадратичной функции.

В начале темы систематизируются сведения о функциях. Повторяются основные понятия: функция, аргумент, область определения функции, график. Даются понятия о возрастании и убывании функции, промежутках знакопостоянства. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа.

Подготовительным шагом к изучению свойств квадратичной функции является также рассмотрение вопроса о квадратном трехчлене и его корнях, выделении квадрата двучлена из квадратного трехчлена, разложении квадратного трехчлена на множители .

Изучение квадратичной функции начинается с рассмотрения функции у = ах², ее свойств и особенностей графика, а также других частных видов квадратичной функции — функций у = ах² + Ь, у = а (х — т)². Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы учащиеся поняли, что график функции у = ах² + Ьх + с может быть получен из графика функции у = ах²с помощью двух параллельных переносов. Приемы построения графика функции у = ах² + Ьх + с отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у учащихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы.

При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак.

Учащиеся знакомятся со свойствами степенной функции у = х^ппри четном и нечетном натуральном показателе п. Вводится понятие корня n-й степени. Учащиеся должны понимать смысл записей вида . Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется

4. Прогрессии (15ч)

Числовые последовательности Способы задания числовых последовательностей (аналитический, словесный, рекуррентный). Свойства числовых последовательностей.

Арифметическая прогрессия. Формула п-ого члена. Формула суммы членов конечной арифметической прогрессии. Характеристическое свойство.

Геометрическая прогрессия. Формула п-ого члена. Формула суммы членов конечной геометрической прогрессии .Характеристическое свойство. Прогрессии и банковские расчеты.

Основная цель — дать понятия об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.

При изучении темы вводится понятие последовательности, разъясняется смысл термина «n-й член последовательности», вырабатывается умение использовать индексное обозначение. Эти сведения носят вспомогательный характер и используются для изучения арифметической и геометрической прогрессий.

Работа с формулами n-го члена и суммы первых п членов прогрессий, помимо своего основного назначения, позволяет неоднократно возвращаться к вычислениям, тождественным преобразованиям, решению уравнений, неравенств, систем.

Рассматриваются характеристические свойства арифметической и геометрической прогрессий, что позволяет расширить круг предлагаемых задач.

5. Элементы комбинаторики, статистики и теории вероятностей (16 ч)

Множества и операции над ними. Комбинаторные задачи. Правило умножения. Факториал. Перестановки.

Группировка информации. Общий ряд данных.Кратность варианты измерений. Табличное представление информации. Частота варианты. Графическое представление информации. Полигон распределения данных. Гистограмма. Числовые характеристики данных измерения (размах, мода, среднее значение).

Вероятность. События (случайное, достоверное, невозможное). Классическая вероятностная схема. Противоположные события. Невозможные события. Вероятность суммы двух событий. Вероятность противоположного события. Статистическая устойчивость. Статистическая вероятность.

Основная цель — ознакомить учащихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события.

Изучение темы начинается с решения задач, в которых требуется составить те или иные комбинации элементов и подсчитать их число. Разъясняется комбинаторное правило умножения, которое используется в дальнейшем при выводе формул для подсчета числа перестановок, размещений и сочетаний.

При изучении данного материала необходимо обратить внимание учащихся на различие понятий «размещение» и «сочетание», сформировать у них умение определять, о каком виде комбинаций идет речь в задаче.

В данной теме учащиеся знакомятся с начальными сведениями из теории вероятностей. Вводятся понятия «случайное событие», «относительная частота», «вероятность случайного события». Рассматриваются статистический и классический подходы к определению вероятности случайного события. Важно обратить внимание учащихся на то, что классическое определение вероятности можно применять только к таким моделям реальных событий, в которых все исходы являются равновозможными

6. Векторы (22ч)

Понятие вектора. Откладывание вектора от данной точки. Откладывание вектора от данной точки. Сумма двух векторов Сумма нескольких векторов. Вычитание векторов. Умножение вектора на число Применение векторов к решению задач Средняя линия трапеции Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в координатах. Решение задач «Метод координат». Уравнение окружности. Уравнение прямой.

Основная цель — научить учащихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов и метода координат при решении геометрических задач.

Вектор определяется как направленный отрезок и действия над векторами вводятся так, как это принято в физике, т. е. как действия с направленными отрезками. Основное внимание должно быть уделено выработке умений выполнять операции над векторами (складывать векторы по правилам треугольника и параллелограмма, строить вектор, равный разности двух данных векторов, а также вектор, равный произведению данного вектора на данное число).

На примерах показывается, как векторы могут применяться к решению геометрических задач. Демонстрируется эффективность применения формул для координат середины отрезка, расстояния между двумя точками, уравнений окружности и прямой в конкретных геометрических задачах, тем самым дается представление об изучении геометрических фигур с помощью методов алгебры

7. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов (12 ч)

Синус, косинус и тангенс угла. Теорема синусов. Теорема косинусов Теорема о площади треугольникаРешение треугольников. Измерительные работы Скалярное произведение векторов. Скалярное произведение векторов в координатах. Применение скалярного произведения векторов к решению задач.

Основная цель — развить умение учащихся применять тригонометрический аппарат при решении геометрических задач.

Синус и косинус любого угла от 0° до 180° вводятся с помощью единичной полуокружности, доказываются теоремы синусов и косинусов и выводится еще одна формула площади треугольника (половина произведения двух сторон на синус угла между ними). Этот аппарат применяется к решению треугольников.

Скалярное произведение векторов вводится как в физике (произведение длин векторов на косинус угла между ними). Рассматриваются свойства скалярного произведения и его применение при решении геометрических задач.

Основное внимание следует уделить выработке прочных навыков в применении тригонометрического аппарата при решении геометрических задач.

8. Длина окружности и площадь круга (10 ч)

Правильный многоугольник. Окружность, описанная около правильного многоугольника и вписанная в правильный многоугольник .Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной. окружности. Длина окружности. Площадь круга и кругового сектора

Основная цель — расширить знание учащихся о многоугольниках; рассмотреть понятия длины окружности и площади круга и формулы для их вычисления.

В начале темы дается определение правильного многоугольника и рассматриваются теоремы об окружностях, описанной около правильного многоугольника и вписанной в него. С помощью описанной окружности решаются задачи о построении правильного шестиугольника и правильного 2га-угольника, если дан правильный /г-угольник.

Формулы, выражающие сторону правильного многоугольника и радиус вписанной в него окружности через радиус описанной окружности, используются при выводе формул длины окружности и площади круга. Вывод опирается на интуитивное представление о пределе: при неограниченном увеличении числа сторон правильного многоугольника, вписанного в окружность, его периметр стремится к длине этой окружности, а площадь — к площади круга, ограниченного окружностью

9. Движения (6 ч)

Понятие движения Свойства движений. Параллельный перенос. Поворот.

Основная цель — познакомить учащихся с понятием движения и его свойствами, с основными видами движений, со взаимоотношениями наложений и движений.

Движение плоскости вводится как отображение плоскости на себя, сохраняющее расстояние между точками. При рассмотрении видов движений основное внимание уделяется построению образов точек, прямых, отрезков, треугольников при осевой и центральной симметриях, параллельном переносе, повороте. На эффектных примерах показывается применение движений при решении геометрических задач. Понятие наложения относится в данном курсе к числу основных понятий. Доказывается, что понятия наложения и движения являются эквивалентными: любое наложение является движенцем плоскости и обратно. Изучение доказательства не является обязательным, однако следует рассмотреть связь понятий наложения и движения

10. Об аксиомах геометрии

Беседа об аксиомах геометрии.

Основная цель — дать более глубокое представление о системе аксиом планиметрии и аксиоматическом методе.

В данной теме рассказывается о различных системах аксиом геометрии, в частности о различных способах введения понятия равенства фигур.

11. Начальные сведения из стереометрии

Предмет стереометрии. Геометрические тела и поверхности. Многогранники: призма, параллелепипед, пирамида, формулы для вычисления их объемов. Тела и поверхности вращения: цилиндр, конус, сфера, шар, формулы для вычисления их площадей поверхностей и объемов.

Основная цель — дать начальное представление о телах и поверхностях в пространстве; познакомить учащихся с основными формулами для вычисления площадей поверхностей и объемов тел. Рассмотрение простейших многогранников (призмы, параллелепипеда, пирамиды), а также тел и поверхностей вращения (цилиндра, конуса, сферы, шара) проводится на основе наглядных представлений, без привлечения аксиом стереометрии. Фор мулы для вычисления объемов, указанных тел выводятся на основе принципа Кавальери, формулы для вычисления площадей боковых поверхностей цилиндра и конуса получаются с помощью разверток этих поверхностей, формула площади сферы приводится без обоснования

12. Повторение учебного материала курса 9 класса (15ч+9ч)
МЕХАНИЗМЫ ФОРМИРОВАНИЯ КЛЮЧЕВЫХ КОМПЕТЕНЦИЙ ОБУЧАЮЩИХСЯ

№п/п	Название разделов	Всего часов	Контрольные работы	Тесты	Проверочные работы	Зачеты
1	Неравенства и системы неравенств	2	1	1
2	Системы уравнений	3	1		1	1
3	Числовые функции.	5	2	3
4	Прогрессии	2	1	1
5	Элементы комбинаторики, статистики и теории вероятностей	3	1	1	1
6	Векторы. Метод координат	3	1		2
7	Соотношение между сторонами и углами треугольника. Скалярное произведение векторов»	2	1		1
8	Длина окружности и площадь круга	2	1		1
9	Движения	2	1		1
10	Итоговое повторение	3		2		1
	ИТОГО	27	10	8	7	2

Требования к уровню подготовки выпускников основной школы

АРИФМЕТИКА

Уметь:

выполнять устный счет с целыми числами, обыкновенными и десятичными дробями;
переходить от одной формы записи чисел к другой, выбирая наиболее подходящую, в зависимости от конкретной ситуации; представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты в виде дроби и дробь в виде процентов; применять стандартный вид числа для записи больших и малых чисел; выполнять умножение и деление чисел, записанных в стандартном виде;
изображать числа точками на координатной прямой;
выполнять арифметические действия с рациональными числами, сравнивать рациональные числа; находить значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближенное значение числового выражения; пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи на движение и работу; задачи, связанные с отношением и с пропорциональностью величин; основные задачи на дроби и на проценты; задачи с целочисленными неизвестными.
Применять полученные знания:
для решения несложных практических расчетных задач, в том числе, с использованием при необходимости справочных материалов и простейших вычислительных устройств; для устной прикидки и оценки результатов вычислений; для проверки результата вычисления на правдоподобие, используя различные приемы; для интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.

АЛГЕБРА

Уметь:

составлять буквенные выражения и формулы по условиям задач, осуществлять подстановку одного выражения в другое, осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, выражать из формул одни переменные через другие;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы уравнений (линейные и системы, в которых одно уравнение второй, а другое первой степени);
решать линейные неравенства с одной переменной и их системы, квадратные неравенства;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, учитывать ограничения целочисленности, диапазона изменения величин;
определять значения тригонометрических выражений по заданным значениям углов;
находить значения тригонометрических функций по значению одной из них;
определять координаты точки в координатной плоскости, строить точки с заданными координатами; решать задачи на координатной плоскости: изображать различные соотношения между двумя переменными, находить координаты точек пересечения графиков;
применять графические представления при решении уравнений, систем, неравенств;
находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу;
строить графики изученных функций, описывать их свойства, определять свойства функции по ее графику;
распознавать арифметические и геометрические прогрессии, использовать формулы общего члена и суммы нескольких первых членов.
Применять полученные знания:
для выполнения расчетов по формулам, понимая формулу как алгоритм вычисления; для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах; при моделировании практических ситуаций и исследовании построенных моделей (используя аппарат алгебры);
при интерпретации графиков зависимостей между величинами, переводя на язык функций и исследуя реальные зависимости;
для расчетов, включающих простейшие тригонометрические формулы;
при решении планиметрических задач с использованием аппарата тригонометрии.

ЭЛЕМЕНТЫ ЛОГИКИ, КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ

Уметь:

оценивать логическую правильность рассуждений, в своих доказательствах использовать только логически корректные действия, понимать смысл контрпримеров;
извлекать информацию, представленную в таблицах, на диаграммах, на графиках; составлять таблицы; строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
вычислять средние значения результатов измерений; находить частоту события;
в простейших случаях находить вероятности случайных событий, в том числе с использованием комбинаторики.

Применять полученные знания:

при записи математических утверждений, доказательств, решении задач;
в анализе реальных числовых данных, представленных в виде диаграмм, графиков;
при решении учебных и практических задач, осуществляя систематический перебор вариантов;
при сравнении шансов наступления случайных событий;
для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией.

ГЕОМЕТРИЯ

Уметь:

распознавать плоские геометрические фигуры, различать их взаимное расположение, аргументировать суждения, используя определения, свойства, признаки;
изображать планиметрические фигуры, выполнять чертежи по условиям задач, осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их; представлять их сечения и развертки;
вычислять значения геометрических величин (длин, углов, площадей, объемов);
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать основные задачи на построение с помощью циркуля и линейки: угла, равного данному; биссектрисы данного угла; серединного перпендикуляра к отрезку; прямой, параллельной данной прямой; треугольника по трем сторонам;
решать простейшие планиметрические задачи в пространстве.

Применять полученные знания:

при построениях геометрическими инструментами (линейка, угольник, циркуль, транспортир);
для вычисления длин, площадей основных геометрических фигур с помощью формул (используя при необходимости справочники и технические средства).

1 2 3 4 5