|
Рабочая программа
по математике
для 9 класса
среднего (полного) общего образования
(базовый уровень)
Составила Дедова Т.В
учитель математики и физики
МКОУ «Синелипяговская СОШ»
с. Синие Липяги - 2013-14
Пояснительная записка
Рабочая программа составлена на основе следующих документов:
Федерального компонента государственного образовательного стандарта основного общего образования по математике 2004 г;
Примерной программы основного общего образования по математике;
Авторской программы по алгебре к учебнику «Алгебра 9 класс», авторы Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова;
Авторской программы к учебнику «Геометрия, 7-9 класс», авторы Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.
Учебного плана МКОУ «Синелипяговская СОШ»
Примерная программа основного общего образования по математике и авторская программа по алгебре и геометрии взяты из методического пособия «Программы общеобразовательных учреждений» АЛГЕБРА 7-9 классы, ГЕОМЕТРИЯ 7-9 классы, составитель: Бурмистрова Т.А Издательство «Просвещение», 2009.
Обучение математике в 9 классе направлено на достижение следующих целей:
Овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования.
Интеллектуальное развитие, продолжение формирований качеств личности, свойственных математической деятельности: ясности и точности мышления, критичности мышления, интуиции как свернутого сознания, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей.
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание культуры личности, внимания как свернутого контроля, отношения к математике как к части общечеловеческой культуры.
Общая характеристика учебного предмета.
Математическое образование в основной школе складывается из следующих содержательных компонентов: алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия – один из важнейших компонентов математического образования. Она необходима для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, развития пространственного воображения и интуиции, математической культуры, эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
В курсе геометрии 9-го класса формируется понятие вектора. Особое внимание уделяется выполнению операций над векторами в геометрической форме. Учащиеся дополняют знания о треугольниках сведениями, о методах вычисления элементов произвольных треугольниках, основанных на теоремах синусов и косинусов. Даются систематизированные сведения о правильных многоугольниках, об окружности, вписанной в правильный многоугольник и описанной. Особое место занимает решение задач на применение формул. Даются первые знания о движении, повороте и параллельном переносе. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Место предмета в учебном плане.
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится не менее 875 ч из расчета 5 ч в неделю с V по IX класс. Математика изучается в 9 классе 5 ч в неделю, всего 175 ч.
Требования к уровню подготовки выпускников 9 класса
Знать/понимать
Существо понятия математического доказательства, приводить примеры доказательств.
Существо понятия алгоритма, приводить примеры алгоритмов.
Как используются математические формулы, уравнения и неравенства, примеры их применения для решения математических и практических задач.
Как математически определенные функции могут описывать реальные зависимости, приводить примеры таких описаний
Как потребности практики привели математическую науку к необходимости расширения понятия числа.
Вероятностный характер многих закономерностей окружающего мира, примеры статистических закономерностей и выводов.
Каким образом геометрия возникла из практических задач землемерия, примеры геометрических объектов и утверждений о них, важных для практики.
Смысл формализации, позволяющий решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при формализации.
Арифметика
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе с использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычислений с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
Уметь
составлять формулу по условию задачи; осуществлять числовые подстановки и выполнять соответствующие вычисления в формулах, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через другую;
применять свойства арифметических корней для вычисления значений и преобразования числовых выражений, содержащих корни;
решать линейные, квадратные и рациональные уравнения, сводящиеся к ним, системы двух уравнений, линейные и несложные нелинейные;
решать линейные и квадратные неравенства и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа на координатной прямой и точки с заданной координатой на координатной плоскости; изображать множество решений неравенства на координатной прямой;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значение функции по ее аргументу, значение аргумента по значению функции;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; находить нужные формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами
Геометрия
уметь
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задачи; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин, в том числе тригонометрических функций; находить стороны, углы и площади треугольников, правильных многоугольников, некоторых четырехугольников, длины ломаных и дуг окружности; находить площади основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами.
Элементы логики, комбинаторики, статистики и теории вероятностей
Уметь
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждения;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятность случайного события в простейших случаях.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве в диалоге;
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности;
решения учебных и практических задач, требующих системного перебора вариантов;
сравнения шансов наступления случайных событий, для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
Содержание программы учебного курса.
Свойства функций. Квадратичная функция
Функция. Свойства функций. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Функция у = ах2 + bх + с, её свойства и график. Степенная функция.
Цель: расширить сведения о свойствах функций, ознакомить обучающихся со свойствами и графиком квадратичной функции.
Уравнения и неравенства с одной переменной
Целые уравнения. Дробные рациональные уравнения. Неравенства второй степени с одной переменной. Метод интервалов.
Цель: систематизировать и обобщить сведения о решении целых и дробных рациональных уравнений с одной переменной, сформировать умение решать неравенства вида ах2 + bх + с>0 или ах2 + bх + с<0, где а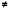 0. 0.
Уравнения и неравенства с двумя переменными
Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы.
Цель: выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и неравества с двумя переменными, и текстовые задачи с помощью составления таких систем.
Прогрессии
Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы первых n членов прогрессии. Бесконечно убывающая геометрическая прогрессия.
Цель: дать понятия об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.
Элементы комбинаторики и теории вероятностей
Комбинаторное правило умножения. Перестановки, размеще�ния, сочетания. Относительная частота и вероятность случайного события.
Цель: ознакомить учащихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события.
Векторы. Метод координат
Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простей�шие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.
Цель: научить обучающихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов и метода координат при решении геометрических задач.
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Синус, косинус и тангенс угла. Теоремы синусов и косину�сов. Решение треугольников. Скалярное произведение векторов и его применение в геометрических задачах.
Цель: развить умение обучающихся применять тригонометрический аппарат при решении геометрических задач.
Длина окружности и площадь круга
Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.
Цель: расширить знание обучающихся о многоугольниках; рассмотреть понятия длины окружности и площади круга и формулы для их вычисления.
Движения
Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. На�ложения и движения.
Цель: познакомить обучающихся с понятием движения и его свойствами, с основными видами движений, со взаимоотношениями наложений и движений.
Об аксиомах геометрии
Беседа об аксиомах геометрии.
Цель: дать более глубокое представление о си�стеме аксиом планиметрии и аксиоматическом методе.
Начальные сведения из стереометрии
Предмет стереометрии. Геометрические тела и поверхности. Многогранники: призма, параллелепипед, пирамида, формулы для вычисления их объемов. Тела и поверхности вращения: цилиндр, конус, сфера, шар, формулы для вычисления их площадей поверхностей и объемов.
Цель: дать начальное представление о телах и поверхностях в пространстве; познакомить учащихся с основными формулами для вычисления площадей поверхностей и объемов тел.
Повторение. Решение задач
Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры и геометрии 7-9 классов.
Перечень контрольных работ.
Контрольная работа №1 по теме «Функции и их свойства».
Контрольная работа №2 по теме «Квадратичная и степенная функции».
Контрольная работа № 3 по теме «Векторы. Метод координат».
Контрольная работа № 4 по теме «Уравнения и неравенства с одной переменной».
Контрольная работа № 5 по теме «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов».
Контрольная работа № 6 по теме «Уравнения и неравенства с двумя переменными»
Контрольная работа № 7 по теме «Длина окружности и площадь круга».
Контрольная работа № 8 по теме «Арифметическая прогрессия».
Контрольная работа № 9 по теме «Геометрическая прогрессия».
Контрольная работа № 10 по теме «Движения».
Контрольная работа № 11 по теме «Элементы комбинаторики и теории вероятностей».
Итоговая контрольная работа.
Календарно тематическое планирование.
№ урока
|
Тема урока
|
Вид контроля
|
Тип урока
|
Дата проведения занятия
|
план
|
факт
|
Глава 1 Квадратичная функция 22часа
|
1
|
Функция. Область определения и область значений функции.
|
|
ИНМ
|
|
|
2
|
Функция. Область определения и область значений функции.
|
|
ЗИМ
|
|
|
3
|
Свойства функций.
|
|
ИНМ
|
|
|
4
|
Свойства функций.
|
|
ЗИМ
|
|
|
5
|
Свойства функций.
|
Самостоятельная работа по теме «Функции и их свойства»
|
ОСЗУ
|
|
|
6
|
Квадратный трёхчлен и его корни.
|
|
ИНМ
|
|
|
7
|
Квадратный трёхчлен и его корни.
|
Математический диктант
|
ЗИМ
|
|
|
8
|
Разложение квадратного трёхчлена на множители.
|
|
ИНМ
|
|
|
9
|
Разложение квадратного трёхчлена на множители.
|
|
ЗИМ
|
|
|
10
|
Контрольная работа №1 по теме «Функции и их свойства».
|
Контрольная работа
|
КЗ
|
|
|
11
|
Функция y=аx2, её график и свойства.
|
|
ИНМ
|
|
|
12
|
Функция y=аx2, её график и свойства.
|
|
ЗИМ
|
|
|
13
|
Графики функций y=аx2+ n u y= a(x-m)2
|
Математический диктант
|
ИНМ
|
|
|
14
|
Графики функций y=аx2+ n u y= a(x-m)2
|
|
ЗИМ
|
|
|
15
|
Графики функций y=аx2+ n u y= a(x-m)2
|
Самостоятельная работа
|
ОСЗУ
|
|
|
16
|
Построение графика квадратичной функции.
|
|
К
|
|
|
17
|
Построение графика квадратичной функции.
|
|
К
|
|
|
18
|
Построение графика квадратичной функции.
|
Практическая работа.
|
ОСЗУ
|
|
|
19
|
Функция y=xn
|
|
ИНМ
|
|
|
20
|
Корень n-й степени.
|
|
ИНМ
|
|
|
21
|
Корень n-й степени.
|
Самостоятельная работа
|
ЗИМ
|
|
|
22
|
Контрольная работа №2 по теме «Квадратичная и степенная функции».
|
Контрольная работа
|
КЗ
|
|
|
Векторы 8часов
|
23
|
Понятие вектора. Равенство векторов
|
|
К
|
|
|
24
|
Откладывание вектора от данной точки.
|
|
К
|
|
|
25
|
Сумма двух векторов.
|
|
К
|
|
|
26
|
Законы сложения векторов. Правило параллелограмма
|
|
К
|
|
|
27
|
Вычитание векторов.
|
Практическая работа по теме «Сложение и вычитание векторов».
|
ОСЗУ
|
|
|
28
|
Произведение вектора на число.
|
|
К
|
|
|
29
|
Применение векторов к решению задач.
|
|
ОСЗУ
|
|
|
30
|
Средняя линия трапеции
|
Практическая работа по теме «Умножение вектора на число».
|
К
|
|
|
Метод координат 10часов
|
31
|
Разложение вектора по двум неколлинеарным векторам.
|
|
К
|
|
|
32
|
Координаты вектора.
|
|
К
|
|
|
33
|
Связь между координатами вектора и координатами его начала и конца.
|
|
К
|
|
|
34
|
Простейшие задачи в координатах.
|
Математический диктант.
|
К
|
|
|
35
|
Уравнение линии на плоскости. Уравнение окружности.
|
|
К
|
|
|
36
|
Уравнение прямой.
|
|
К
|
|
|
37
|
Уравнения окружности и прямой.
|
Самостоятельная работа.
|
К
|
|
|
38
|
Решение задач.
|
|
ОСЗУ
|
|
|
39
|
Решение задач.
|
|
ОСЗУ
|
|
|
40
|
Контрольная работа № 3 по теме «Векторы. Метод координат».
|
Контрольная работа
|
КЗ
|
|
|
Уравнения и неравенства с одной переменной 14часов
|
41
|
Целое уравнение и его корни.
|
|
ИНМ
|
|
|
42
|
Целое уравнение и его корни.
|
|
ЗИМ
|
|
|
43
|
Целое уравнение и его корни.
|
Самостоятельная работа.
|
К
|
|
|
44
|
Дробные рациональные уравнения.
|
|
ИНМ
|
|
|
45
|
Дробные рациональные уравнения.
|
|
К
|
|
|
46
|
Дробные рациональные уравнения.
|
|
К
|
|
|
47
|
Дробные рациональные уравнения.
|
|
К
|
|
|
48
|
Дробные рациональные уравнения.
|
Самостоятельная работа.
|
ОСЗУ
|
|
|
49
|
Решение неравенств второй степени с одной переменной.
|
|
ИНМ
|
|
|
50
|
Решение неравенств второй степени с одной переменной.
|
|
ЗИМ
|
|
|
51
|
Решение неравенств методом интервалов.
|
|
ИНМ
|
|
|
52
|
Решение неравенств методом интервалов.
|
|
ЗИМ
|
|
|
53
|
Решение неравенств методом интервалов.
|
Самостоятельная работа.
|
ОСЗУ
|
|
|
54
|
Контрольная работа № 4 по теме «Уравнения и неравенства с одной переменной».
|
Контрольная работа
|
КЗ
|
|
|
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов 11часов
|
55
|
Синус, косинус, тангенс угла. Основное тригонометрическое тождество. Формулы приведения.
|
|
ИНМ
|
|
|
56
|
Формулы для вычисления координат точки.
|
|
К
|
|
|
57
|
Синус, косинус и тангенс. Решение задач.
|
Самостоятельная работа
|
К
|
|
|
58
|
Теорема о площади треугольника.
|
|
ИНМ
|
|
|
59
|
Теоремы синусов и косинусов.
|
|
ИНМ
|
|
|
60
|
Решение треугольников.
|
|
К
|
|
|
61
|
Решение треугольников. Измерительные работы.
|
|
К
|
|
|
62
|
Угол между векторами. Скалярное произведение векторов.
|
|
ИНМ
|
|
|
63
|
Скалярное произведение в координатах. Свойства скалярного произведения векторов.
|
Самостоятельная работа
|
К
|
|
|
64
|
Соотношения между сторонами и углами треугольника. Решение задач.
|
|
К
|
|
|
65
|
Контрольная работа № 5 по теме «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов».
|
Контрольная работа
|
КЗ
|
|
|
Уравнения и неравенства с двумя переменными 17часов
|
66
|
Уравнение с двумя переменными и его график.
|
|
ИНМ
|
|
| |
|
|
 Скачать 451.14 Kb.
Скачать 451.14 Kb. 0.
0.