Применение геометрических методов при решении задач на движение

Скачать 47.13 Kb. Название Применение геометрических методов при решении задач на движение Дата 05.03.2016 Размер 47.13 Kb. Тип Задача

Маркова Т.В. учитель математики МБОУ города Дубны МО лицей №6 имени академика Г.Н.Флерова Применение геометрических методов при решении задач на движение. Одной из актуальных проблем школьного математического образования на современном этапе является проблема интеграции математических знаний, формирования целостных представлений учащихся о математике как науке. Понятие “интеграция” следует понимать как объединение в целое элементов математических знаний, способность использовать их в различных ситуациях, применять математический аппарат при изучении смежных дисциплин, а также как процесс, ведущий к такому состоянию. Основным видом деятельности учащихся при обучении математике является решение задач, а значит целесообразно интеграцию алгебры и геометрии осуществлять по линии их методов. Надо отметить, что большинство учащихся знакомы с применением метода уравнений и неравенств при решении геометрических задач и почти никто не пытается применить геометрические методы в алгебре. Часто именно по этой причине выпускники не справляются с решением задач части С в ЕГЭ. В области обучения решению задач интеграция методов предполагает параллельное (на одном уроке) решение задачи разными методами или решение задачи более удобным, “нетрадиционным” методом. На уровне 8 класса учащиеся уже решаю достаточно сложные текстовые задачи, большое их количество содержит учебник, кроме того изученный геометрический материал богат и разнообразен. Все это дает возможность применить при решении сложных текстовых задач на движение графический метод, основанный на знании законов геометрии (метод треугольников и подобия треугольников) . Задача 1 (№ 564, алгебра 8, Ш.А. Алимов) Из пункта А в пункт В отправился автомобиль, а одновременно навстречу ему из пункта В отправился автобус. Автомобиль прибыл в пункт В через 40 мин после встречи с автобусом, а автобус прибыл в пункт А через 1,5 часа после их встречи. Найти скорость автомобиля и автобуса, если расстояние от А до В 100 км. 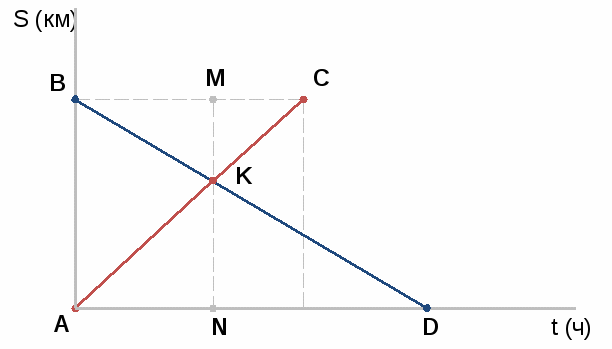40 мин = – время в пути автомобиля после встречи с автобусом до прибытия в пункт В. 1,5 ч – время в пути автобуса после встречи с автомобилем до прибытия в пункт А. 1) АВ = 100 км. Пусть AN = t, точка К соответствует встрече, тогда МС = , а ND = 1,5. ∆ ANK ~ ∆ CMK и ∆ DNK ~ ∆ BMK , значит . t : = 1,5 : t; t2 = · 1,5; t2 = 1 t = ± 1 ( -1 не подходит по смыслу задачи ), t = 1 1 ч прошел до встречи автомобиля и автобуса. 2) 1 + = 1 (ч) – ехал автомобиль от пункта А до пункта В 3) 100 : 1 = = 60 (км/ч) – скорость автомобиля 4) 1 + 1,5 = 2,5 (ч) – ехал автобус от пункта А до пункта В 5) 100 : 2,5 = = 40 (км/ч) – скорость автобуса Ответ: 40 км/ч, 60 км/ч Аналогично: № 835 (Ш.А. Алимов. Алгебра 8) №№ 7.2, 7.34, 7.35, 7.36 (Л.В. Кузнецова. Алгебра. Сборник заданий для подготовки к итоговой аттестации в 9 классе). Задача 2 (№ 8) Дрессировщик занимается с пони на арене цирка. По сигналу пони скачут в разные стороны друг от друга. Первая пони двигалась быстрее и поэтому к моменту встречи пробежала на 5 м больше второй и, продолжив движение, добежала до дрессировщика за 9 сек с момента встречи, а вторая – за 16 сек после встречи. Каков диаметр арены?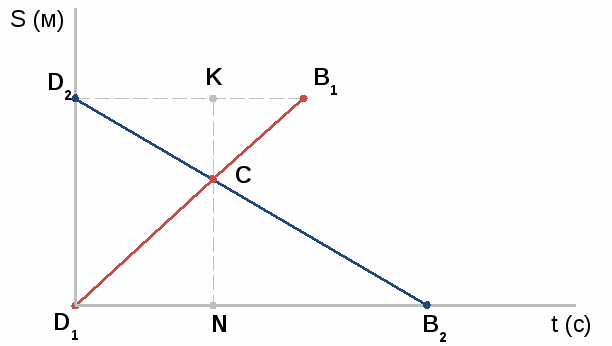 Если окружность, соответствующую границе арены, разрезать в точке, где стоит дрессировщик (D) и развернуть, то концы отрезка обозначим D1, D2. Пусть V1 > V2 , значит CN больше СК на 5, т.е. CN = СК + 5, В1К= 9, В2N = 16. 1) ∆ D1NC ~ ∆ B1KC = и ∆ В2NC ~ ∆ D2KC = , значит = . Пусть D1N = D2K = t, тогда: , t2 = 9 · 16, t = ±12 ( -12 не подходит по смыслу задачи ), t = 12 12 сек прошло до момента встречи пони 2) Пусть СК = х, тогда CN = х + 5 Так как = , то , 3х + 15 = 4х, х = 15 15 м проскакала вторая пони до момента встречи 3) NК = СК + CN = х + х + 5 = 35 (м) NК = D1D2 = С – длина окружности арены С = 2πr, C = πd, d = м – диаметр арены Ответ: м Аналогично: № 832, 833, 834 (Ш.А. Алимов. Алгебра 8) П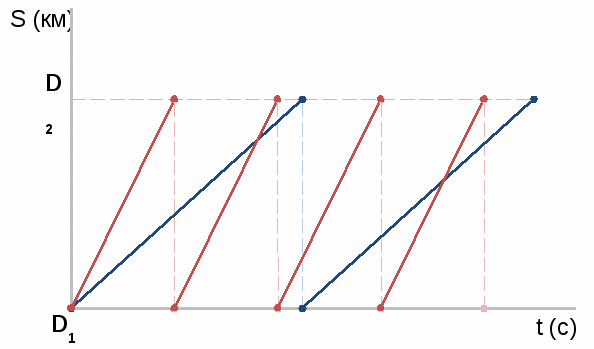ри самостоятельном составлении задач возможны другие ситуации. На рисунке изображен вариант, когда пони бегут в одном направлении, с разными постоянными скоростями. Задача 3 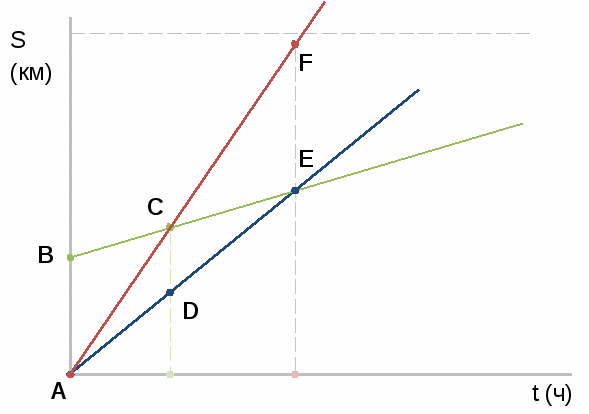Велосипедист и мотоциклист одновременно выезжают из пункта А в сторону пункта В, расстояние между которыми 6 км. Одновременно сними из пункта В выходит пешеход и движется в том же направлении, что и мотоциклист с велосипедистом. В момент, когда мотоциклист догнал пешехода, велосипедист находился от них на расстоянии з км. На каком расстоянии от велосипедиста и пешехода будет находиться мотоциклист в момент, когда велосипедист догонит пешехода? ∆ AВЕ ~ ∆ DCЕ = = ВЕ = 2CD ВС =СЕ ∆ АВС = ∆ FEC ( _ ) . Значит FE =АВ = 6 км Ответ: 6 км Возможно усложнить условие ( СD = 2 км ). В этом случае во второй части задачи опять опираемся на подобие треугольников В качестве домашнего задания можно поменять в условии FE = 2 км. Найти CD. При самостоятельном составлении задач возможны другие ситуации: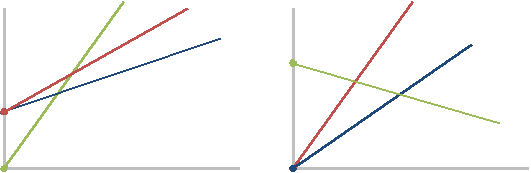