Главная страница
Анализ
Анкета
архив
Биография
Бюллетень
Викторина
Глава
Диплом
Доклад
Документация
Задача

Методическая разработка урока в 10 классе «Тригонометрические уравнения.»



Скачать 26.45 Kb.
НазваниеМетодическая разработка урока в 10 классе «Тригонометрические уравнения.»
Дата05.04.2016
Размер26.45 Kb.
ТипМетодическая разработка

Методическая разработка урока в 10 классе « Тригонометрические уравнения.»

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 5

Краснодарского края Красноармейского района


учитель математики Белик П.И.
Цель:

  1. разобрать два метода решения тригонометрических уравнений: метод подстановки и метод разложения;

  2. закрепить решения простейших тригонометрических уравнений.

Оборудование:

  1. макет единичной окружности;

  2. таблица тригонометрических формул;

Ход урока:

  1. Повторение.

  1. двое учащихся у доски: решение уравнений вида ,

  2. проверка домашнего задания № 348 (в): вычислить

  3. устный счет:

а) по макетам единичной окружности:





























Найти все числа, которым на числовой окружности соответствует точка (точка показывается цветной иголкой).

б) найти ошибки в решениях тригонометрических уравнений: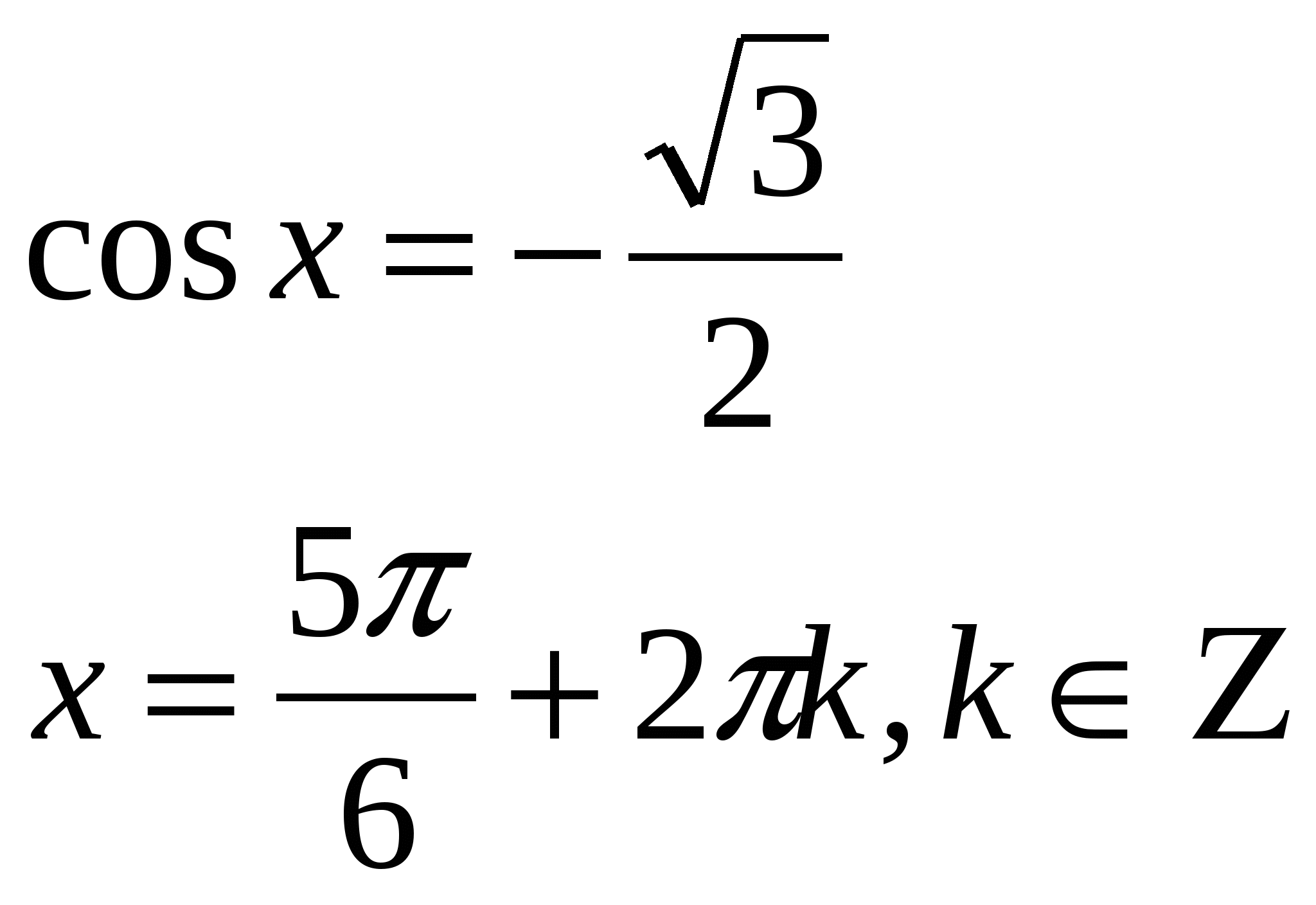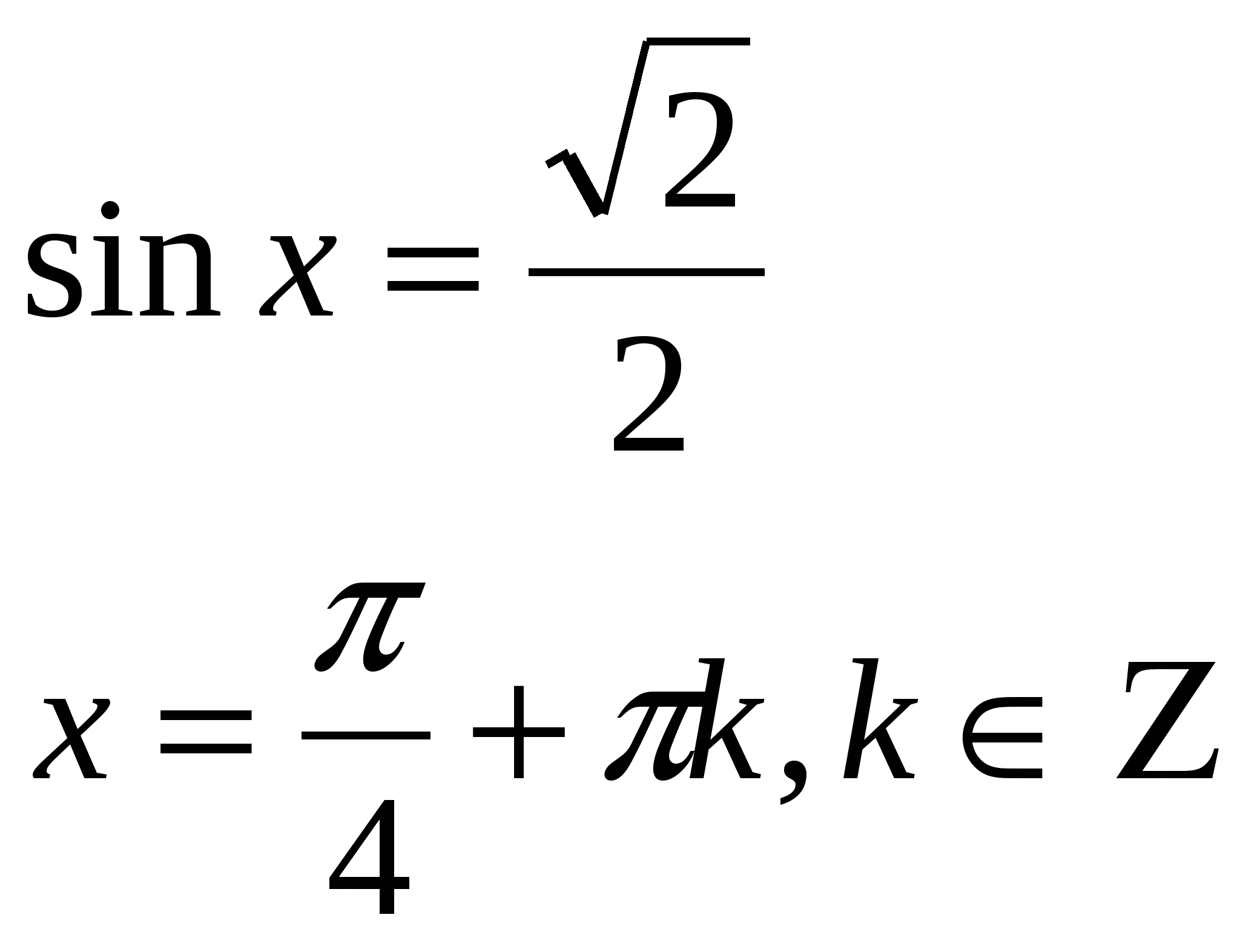




в) разложить на множители:



  1. Объяснение новой темы.


1). Объявить тему и цель урока.

2). Дать определение тригонометрического уравнения.

3). Повторить решения простейших тригонометрических уравнений:

а) проверить работу двух учащихся на доске: решение уравнений вида ,

б) устно вспомнить решения уравнений вида

4). Разберем метод подстановки.

Методом подстановки решаются те тригонометрические уравнения, которые представляют собой квадратные уравнения относительно какой-либо тригонометрической функции. Если в уравнение входят различные тригонометрические функции, то надо выразить их через одну.

а) Разбор учителем уравнения:



Т.к. 8 – (–1) + (–9)=0, то





б) Решение уравнения из № 355 (б) на доске одним из учеников, остальные работают в тетрадях.

Ответ:

в) № 356 (б) самостоятельно на местах с последующей проверкой: Ответ: .

г) № 358 (б) на доске.

Ответ:

5). Разберем метод разложения на множители.

а) Разбор учителем уравнения: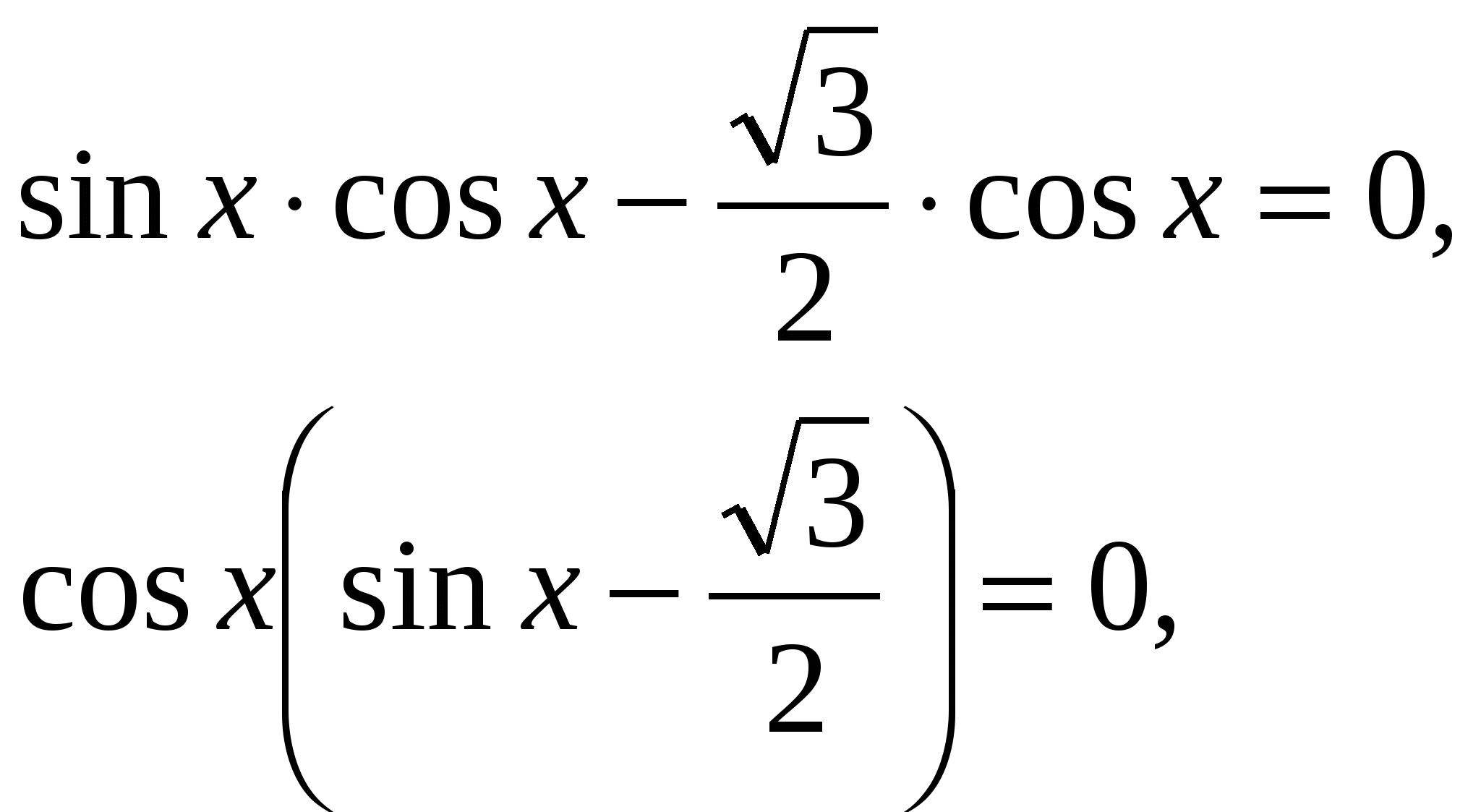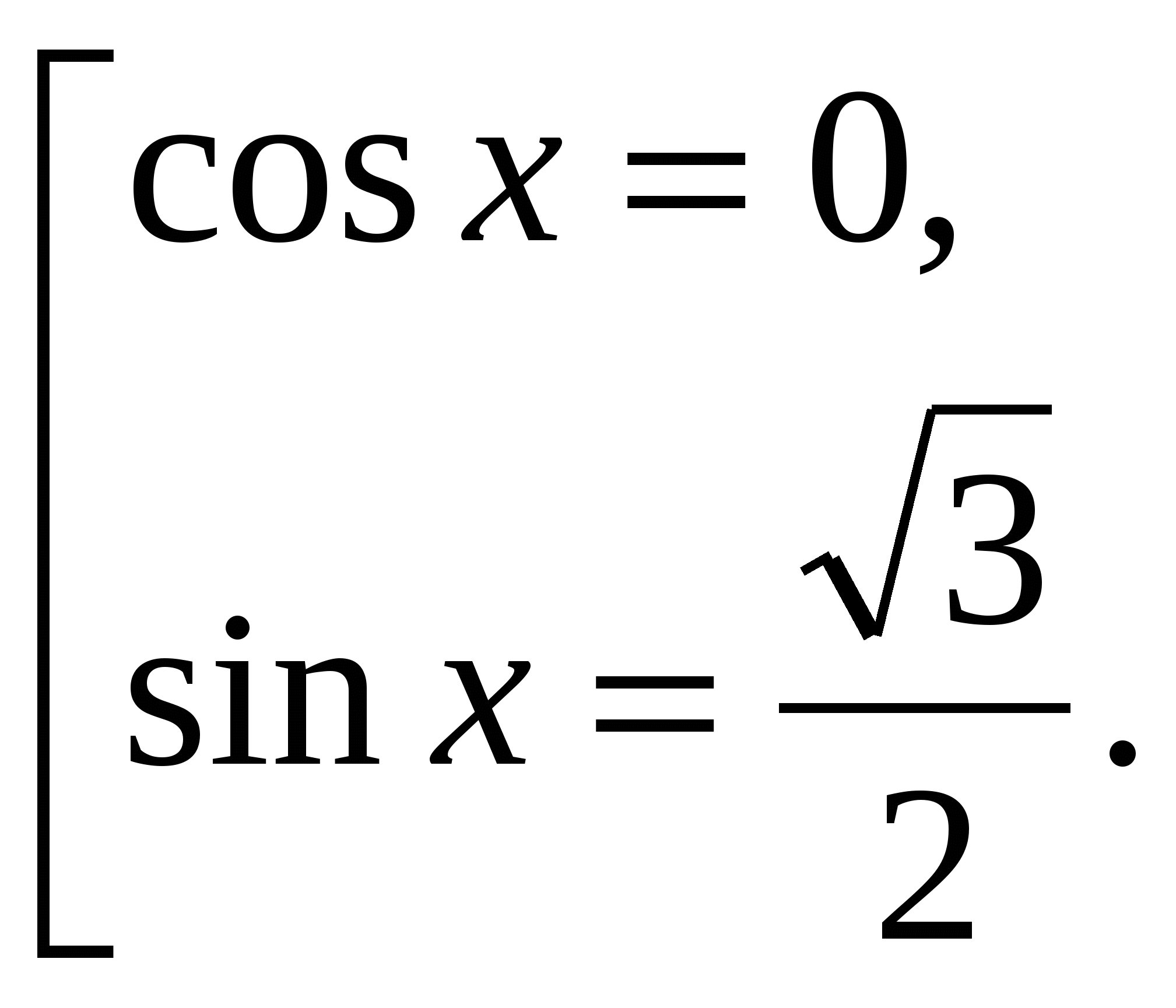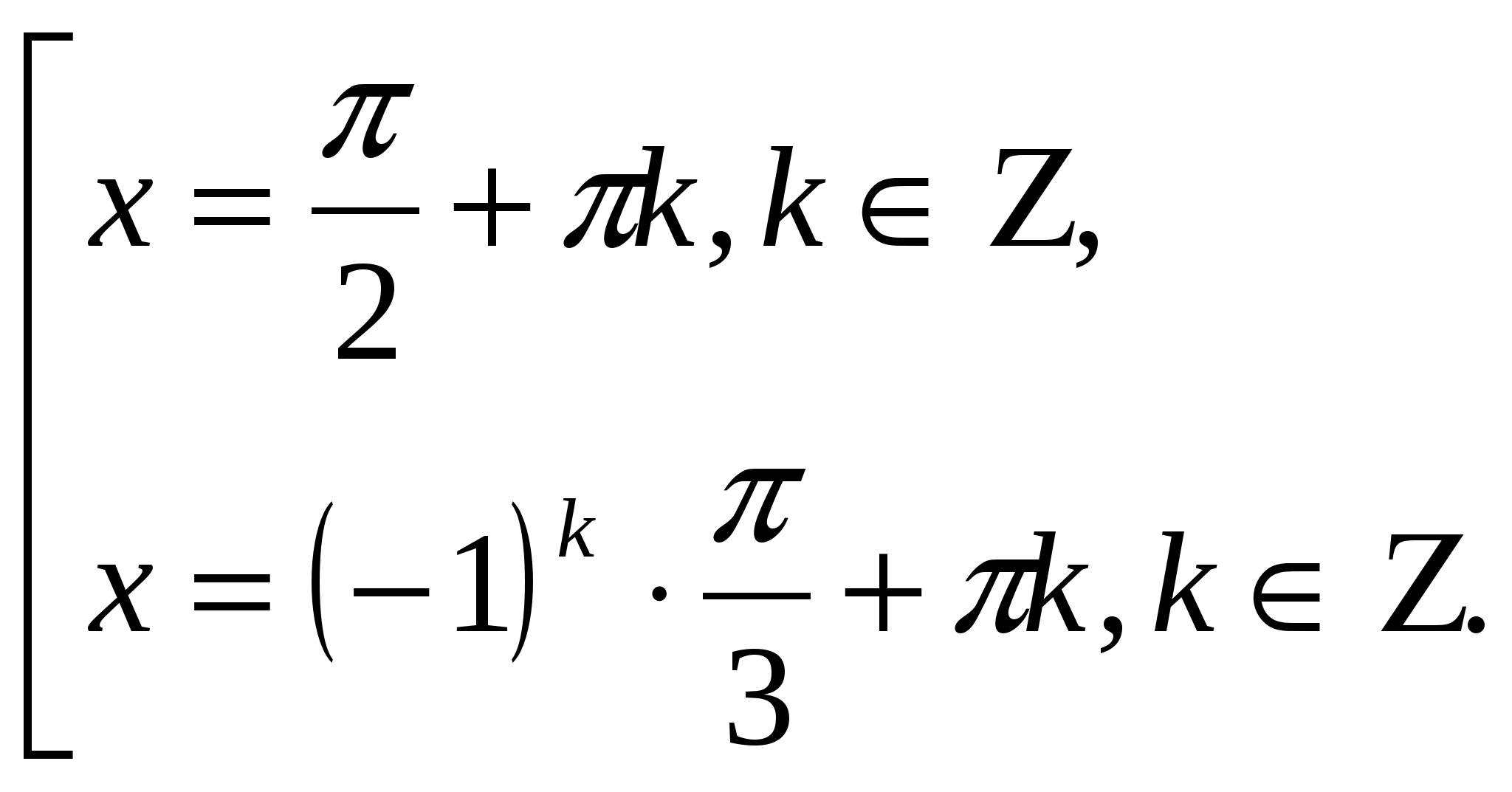





б) № 373 (а) на доске.

Ответ:

№ 373 (в) самостоятельно, один ученик на доске.

Ответ:

  1. Домашнее задание:

п. 20(2), № 355-356 (в), № 358 (в), № 359 (в).


  1. Подведение итогов урока:

  1. оценить работу некоторых активных учащихся;

  2. контрольные вопросы: дать определение тригонометрических уравнений; назвать методы решения тригонометрических уравнений, разобранных на сегодняшнем уроке.