План урока по алгебре и началам анализа в 10 классе по теме: Учитель математики: Назарова
 Скачать 46.56 Kb.
|
| Муниципальное бюджетное образовательное учреждение «Гимназия №3» План урока по алгебре и началам анализа в 10 классе по теме:  Учитель математики: Назарова М.А. 2011 – 2012 уч. год. Тема: Преобразование тригонометрических выражений. Цели урока : образовательные: повторить основные формулы тригонометрии, закрепить их знание в ходе выполнения упражнений, обобщить и систематизировать материал по данной теме; развивающие: развить внимание, логическое мышление, самостоятельность и творческий подход к преобразованию выражений. воспитательные: привитие интереса к предмету, формирование умения аккуратно и грамотно выполнять математические записи. Оборудование: интерактивная доска, мультимедийный проектор, карточки, наглядное пособие, учебник "Алгебра и начала анализа, 10 - 11 класс", А.Н.Колмогоров. Ход урока. I). Организационный момент: (приветствие класса, ознакомление учащихся с целями урока) II). Актуализация опорных знаний. 1) Задание на внимание 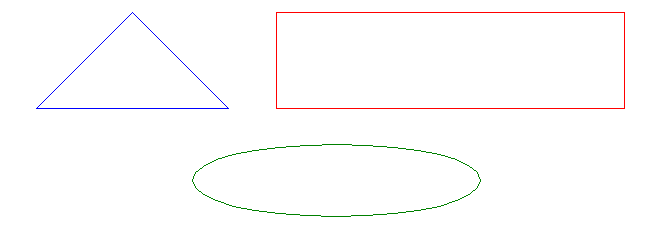 В треугольнике учителем записано выражение Sin 3α, в прямоугольнике Sin 2π + Cos  + Cos  , в эллипсе ctg  (на усмотрение учителя)Учитель несколько секунд показывает карточку с заданием классу, а затем убирает ее и задает вопросы: 1. В какой фигуре записано значение  ?2. Котангенс какого угла равен ?3. Чему равен аргумент синуса, и в какой фигуре это записано? 4. Чему равен Sin 3α? 5. Каким цветом изображен прямоугольник? 6. Найдите значение выражения, записанного в прямоугольнике? 2) Работа на интерактивной доске. Учитель предлагает учащимся повторить тригонометрические формулы с использованием электронного образовательного ресурса (ЭОР). (Применение основных тригонометрических формул к преобразованию выражений, (N 191997) , https://school-collection.edu.ru/catalog/rubr/164c80ce-6e8a-48ff-8b3d-767f851bfe51/112899/ ) 3) Устная работа. Второй и третий ряд работают устно, ученики, сидящие на первом ряду работают по индивидуальным карточкам. К – 1 К – 2 К – 3 1.Заполнить пропуски. 1. Заполнить пропуски. 1.Заполнить пропуски. Sin2 α +Cos2 α =…. Cos 3α = ….  = …..2. Упростить. 2. Упростить. 2. Найти значение.    К – 4 К – 5 К – 6 1.Заполнить пропуски. 1.Заполнить пропуски. 1.Заполнить пропуски. Sin 2α = …. Cos α + Cos β = …… tg α ctg α = ….. 2. Упростить. 2. Упростить. 2. Упростить.  Найти Sin 2α, если Cos α = 7 Cos2α + 7 Sin2α - 5 = 0,2 , α - угол 1 четверти. Задания для устной работы 1. Упростить. a) (1– Sin α)(1+ Sin α); б) Sin 30˚ ctg 30˚ – Cos 30˚; в) Cos α Cos 3α – Sin α Sin 3α; 2. Найти наибольшее значение выражения. tg αCos α + Sin α После третьего задания устной работы первый ряд присоединяется к фронтальной работе. 4) Задание на повторение темы «Преобразование графиков тригонометрических функций». Задание представлено вниманию учащихся в виде презентации. Во время этой работы сильный ученик работает на доске по карточке. * Выразить Sin α через  . (проверка решения после выполнения задания на повторения)Ответ:  III). Отработка знаний, умений, навыков. Ребята, математика, как и другая наука, дала миру огромное количество ученых от древности до наших дней, смысл жизни которых состоял в продвижении науки вперед, в открытии новых закономерностей, формул, доказательств теорем. Выполнив несколько заданий, вы сможете назвать имя древнегреческого ученого, астронома и математика, который составил таблицы хорд – первые тригонометрические таблицы (таблицы синусов от 0˚ до 90˚). Первую букву в его имени вы уже можете назвать, отыскав выражение, полученное при выражении Sin α через .
А П Е Г 4 Sin 25˚ Cos 33˚ Cos 27˚ 1  Х Н И Р Д  Cos 2α  4 Sin 20˚ Cos 12˚ Cos 8˚  1) Упростить:  Ответ: (работают вместе с учителем)2) Ученики работают в тетрадях по вариантам, после выполняют проверку с обменом тетрадей. (решение заранее записано на закрытой части доски). В – 1 (№ 13, в) В – 2 (№ 9, в) Найти числовое значение выражения  Ответ: 1  Ответ: 13). Работа по вариантам. Представители от первого и второго варианта выполняют задание на доске с комментированием, остальные работают в тетрадях В – 1 В – 2 Представить в виде произведения. Sin 19˚ + Sin 25˚+ Sin 31˚ Sin 16˚ + Sin 24˚ + Sin 40˚ Ответ: 4 Sin 25˚ Cos 33˚ Cos 27˚ Ответ: 4 Sin 20˚ Cos 12˚ Cos 8˚ Устно: 4 Sin15˚ Cos 15˚ (Cos215˚ – Sin215˚) Ответ: Ребята вписывают угаданные буквы и называют имя древнегреческого ученого! (Гиппарх) IV). Дифференцированная самостоятельная работа. Учащиеся оценивают свои знания по теме и выбирают задания, соответствующие их оценке. "3" "4" "5" Упростить: 1.Доказать что: Упростить: а) (1 – Sin2 α) (1 + ctg2 α);  а)  ;б)  ; 2. Упростить: б) Cos α – 2 Sin 3α – Cos 5αв)  . Sin α + 2 Sin 2α + Sin 3αV). Итог урока. (ученики в оценочных листах проставляют себе оценки по каждому виду работы.) VI). Домашнее задание. № 24, № 10 (б), № 21 (г), дополнительное задание со звездочкой стр.93, № 9 (3(а, в)). |