Цель урока: совершенствование практических навыков решения задач на комбинацию окружности и многоугольников и умение применять их при решении задач повышенной сложности (вида С26 ГИА)
Планируемые результаты:
Предметные: уметь в процессе решения задач повышенной трудности использовать основные теоретические факты и формулы и умения решать основные типы задач на комбинацию окружности и многоугольников
Личностные: уметь работать в парах, группах, слушать собеседника и вести диалог, аргументировать свою точку зрения
Метапредметные: уметь обрабатывать информацию; формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности.
Задачи:
Образовательные: формирование познавательных УУД :обеспечить осознанное усвоение методов решения задач на комбинацию окружности и многоугольников; закрепить навыки и умения применять алгоритмы при решении задач на комбинацию окружности и многоугольников; систематизация, обобщение и углубление знаний учащихся при решении задач на комбинацию окружности и многоугольников
Воспитательные: формирование коммуникативных и личностных УУД: умение слушать и вступать в диалог,
организовывать работу в микрогруппе; развивать внимательность в вычислениях; воспитывать чувство взаимопомощи, уважительное отношение к чужому мнению, культуру учебного труда, требовательное отношение к себе и своей работе.
Развивающие: формирование регулятивных УУД: повысить познавательный интерес к предмету, развитие логического мышления и способности рассуждать.
Тип урока: обобщение знаний и умений
Формы работы учащихся: фронтальная, парная, групповая, индивидуальная
Необходимое оборудование: карточки самооценивания, мобильный класс, документ- камера, АРМ учителя
Структура и ход урока:
Этап урока
|
Задачи этапа
|
Деятельность учителя
|
Деятельность учеников
|
Формируемые УУД
|
Организационный этап
|
Создать благоприятный психологический настрой на работу
|
Приветствие, проверка подготовленности к учебному занятию, организация внимания детей
|
Включаются в деловой ритм урока
|
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками
Регулятивные: организация своей учебной деятельности
Личностные: мотивация учения
|
Постановка цели и задач урока. Мотивация учебной деятельности учащихся
|
Обеспечить мотивацию учения и принятие обучающимися целей урока
|
Мотивирует учащихся: определяет вместе с ними цель урока, акцентирует внимание учащихся на значимость темы
|
Выдвигают предположение, определяют тему и цель урока, выполняют запись в тетради.
|
Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме
Личностные: самоопределение
Регулятивные: целеполагание
Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса
|
Актуализация знаний
|
Актуализация опорных знаний и способов действий
|
Организация повторения основных теоретических положений и формул, используемых при решении задач на комбинацию окружности и многоугольников
|
Участвуют в работе по повторению: выполняют практическое задание, в беседе с учителем отвечают на поставленные вопросы
|
Познавательные: структурирование собственных знаний, умение работать с ноутбуком;
Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками
Личностные: оценивание усваиваемого материала
Регулятивные: контроль и оценка процесса и результатов деятельности
|
Применение знаний и умений в новой ситуации
|
Показать применение различных способов и методов в решении задач повышенной трудности на примере С26 ГИА
|
Организация и контроль за процессом решения задач
|
Работают в парах и группах над поставленными задачами
|
Познавательные: формирование интереса к данной теме
Личностные: формирование готовности к самообразованию
Коммуникативные: уметь оформлять свои мысли в устной форме, слушать и понимать речь других
Регулятивные: планирование своей деятельности для решения поставленной задачи, контроль и коррекция полученного результата.
|
Контроль усвоения, обсуждение допущенных ошибок и их коррекция
|
Дать качественную оценку работы класса и отдельных учащихся на уроке
|
Выявляет качество и уровень усвоения знаний, устанавливает причины выявленных ошибок
|
Анализируют свою работу, высказывают затруднения и обсуждают правильность решения предложенных задач
|
Личностные: формирование позитивной самооценки;
Коммуникативные: умение слушать и вступать в диалог;
Регулятивные: умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы
|
Информация о домашнем задании
|
Обеспечение понимания учащимися содержания и способов выполнения домашнего задания
|
Даёт комментарий к домашнему заданию
|
Записывают задания в дневник
|
|
Рефлексия (подведение итогов урока)
|
Дать количественную оценку работы учащихся на уроке
|
Подводит итоги работы групп и класса в целом
|
Сдают карточки самооценивания
|
Регулятивные: оценивание собственной деятельности
|
Ход урока
Деятельность учителя
|
Деятельность ученика
|
Организационный этап
Учитель приветствует учащихся, проверяет их готовность к уроку.
У каждой группы на столе лежит карточка самооценивания. Впишите фамилии участников группы. В течение урока мы будем выполнять различные задания. По окончании решения каждой задачи вы должны оценить свою работу:
«+»- справился с задачей без затруднений
«+»- справился с задачей, но возникали сложности
«-»- не справился с задачей
|
Учащиеся слушают учителя
В течение урока после выполнения каждого задания учащиеся оценивают результаты своей деятельности в карточке самооценивания
|
Постановка цели и задач урока. Мотивация учебной деятельности учащихся
Задание: Откройте, пожалуйста, файл с названием «Рисунки» и скажите, о какой теме сегодня пойдёт речь.
Через месяц мы сдаём экзамен, и его результат будет связан с решением задач определённого уровня сложности. Какой уровень нам надо освоить и под каким номером задачи этого уровня предложены в экзаменационных текстах?
Итак, сформулируйте тему урока.
Цель нашего урока — обобщить знания по теме «Комбинация окружности и многоугольника» и суметь применить их при решении задач повышенной сложности.
|
Ответ: Взаимное расположение окружности и многоугольников.
Ответ: задачи повышенной сложности, С26
Ответ: «Задачи повышенной сложности на комбинацию окружности и многоугольника»
Выполняют запись в тетради.
|
Актуализация знаний
Приём «Корзина идей»
В Мимио-блокноте открыть файл с рисунками задач.
• Работа в группах по заданию: выбрать из печатного списка теории только те утверждения, которые подходят по смыслу условия и предполагаемого решения задачи. Номера выбранных утверждений перенести в корзину, остальные оставить на месте.
• Решить каждую задачу в черновике, записать ответы в бланке.
|
Проверяют бланки ответов других групп, обсуждают ошибки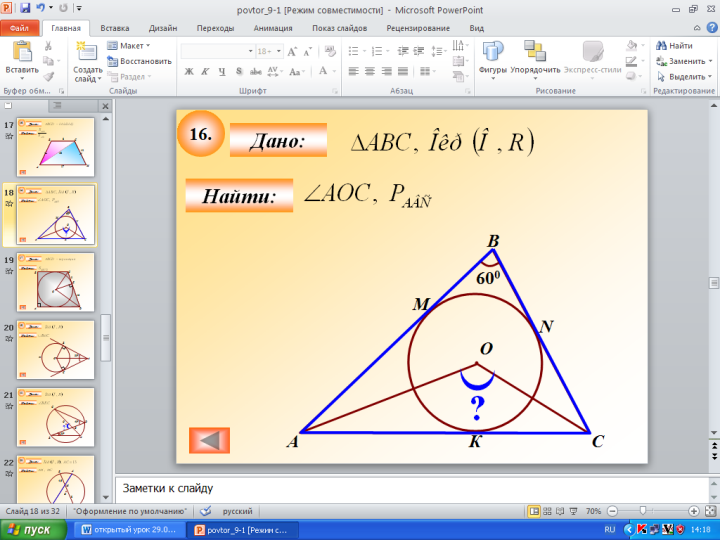
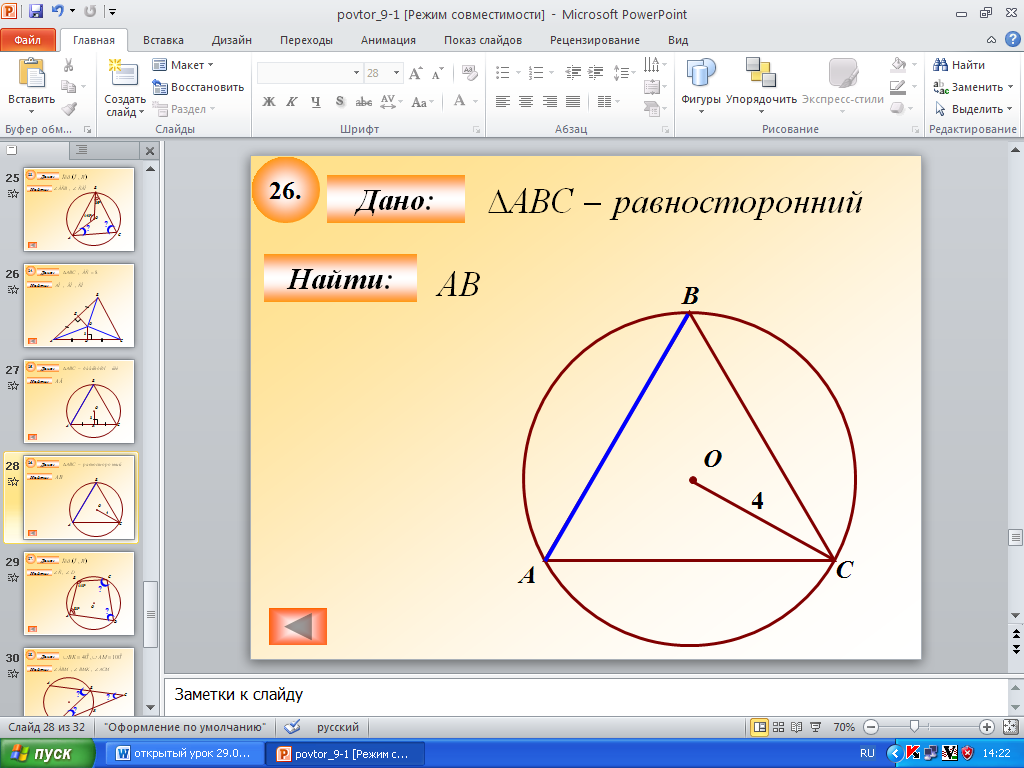 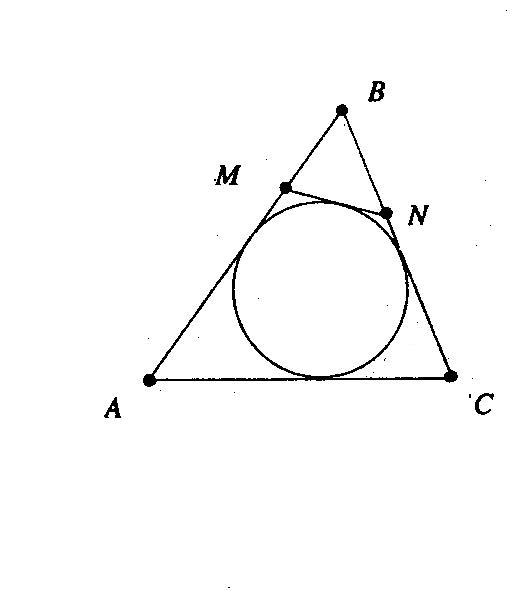
|
Применение знаний и умений в новой ситуации
Приступаем к решению задач типа С26 ГИА
Гущин «Решу ГИА», № 311704 , № 311664
|
Открывают страницу учителя. Работают по тексту задачи над чертежом и условием.
Работа со страницей учителя.
Проверка чертежей через Мимио
Дорешивают задачи до конца с объяснением, проверка - через документ-камеру.
|
Контроль усвоения, обсуждение допущенных ошибок и их коррекция
Егерев В.К. и др. Сборник задач по математике для поступающих в вузы/ Под ред. М.И.Сканави.- К.:Каннон, 1997, задача №10.369, №10.386, №10.372
|
Учащиеся анализируют свою работу, проговаривают вслух свои затруднения, обсуждают правильность решения.
Критерии оценивания:
Задача №1 - «3», №10.372
Задача №2 - «4 , №10.369
Задача №3 - «5», №10.386
|
Информация о домашнем задании
Вам предлагается выбрать задачи разных уровней сложности и соответственно разных критериев оценивания.
|
Выбор задач из распечатки
|
Рефлексия (подведение итогов урока)
Какие способы действий, правила сегодня вы запомнили лучше всего? С каждым учебным годом задачи становятся всё труднее, но и вы приобретаете новые знания, которые помогут вам справиться с любыми трудностями.
Собирает карточки самооценивания, выставляет оценки за работу.
|
Учащиеся сдают карточки самооценивания
|
Приложение1. Карточка самооценивания № группы__________, руководитель__________________________________
ФИ учащегося
|
«+»- справился с задачей без затруднений
|
«+, - »- справился с задачей, но возникали сложности
|
«-»- не справился с задачей
|
|
Тест «Вписанная окружность»
|
|
|
|
«Корзина идей»
|
|
|
|
№ 311704
|
|
|
|
№311664
|
|
|
|
Впишите номер выбранной задачи:
|
|
|
|
2. Теоретические факты
Свойство отрезков касательных к окружности
Свойство четырёхугольника, вписанного в окружность
Свойство четырёхугольника, описанного около окружности
Расширенная теорема синусов
Свойство равных хорд окружности
Вычисление углов в окружности
Расположение центра окружности, описанной около многоугольника
Расположение центра окружности, вписанной в многоугольник
Свойства углов при параллельных прямых и секущей
10. Формулы для вычисления площади четырёхугольника
11. Свойства равнобедренной трапеции
12. Пропорциональные отрезки в прямоугольном треугольнике
3. Тест по теме «Вписанная окружность»Вариант 1.
1. Центр вписанной в треугольник окружности совпадает с точкой пересечения его ….
А) медиан; Б) биссектрис; В) серединных перпендикуляров.
2. Центр вписанной в треугольник окружности равноудалён от …..
А) сторон Б) углов; В) вершин треугольника.
3. Центр вписанной в треугольник окружности является точкой пересечения его медиан. Этот треугольник ….
А) прямоугольный Б) равнобедренный; В) равносторонний.
4. Окружность называется вписанной в многоугольник, если….
А) все его стороны касаются окружности;
Б) все его вершины лежат на окружности;
В) все его стороны имеют общие точки с окружностью.
Таблица ответов:
-
Вариант 2.
1. Радиус вписанной в треугольник окружности равен расстоянию от центра окружности до ….
А) сторон треугольника Б) вершин треугольника; В) углов треугольника.
2. Центр вписанной в равнобедренный треугольник окружности может лежать …..
А) на любой из его высот; Б) на одной из его медиан;
В) на любом из его серединных перпендикуляров.
3. Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Этот треугольник может быть….
А) разносторонним Б) только равносторонним; В) только прямоугольным.
4. Многоугольник называется описанным около окружности, если….
А) окружность имеет общие точки с его сторонами
Б) окружность проходит через его вершины;
В) окружность касается всех его сторон.
Таблица ответов:
-
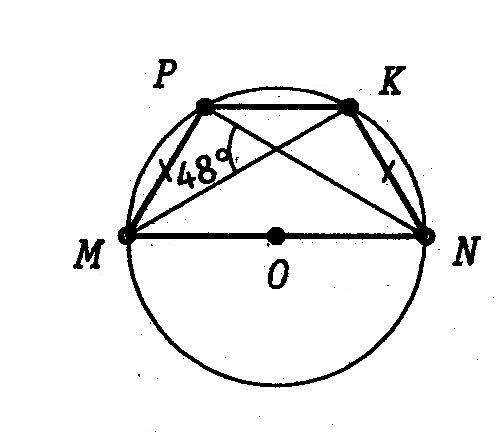
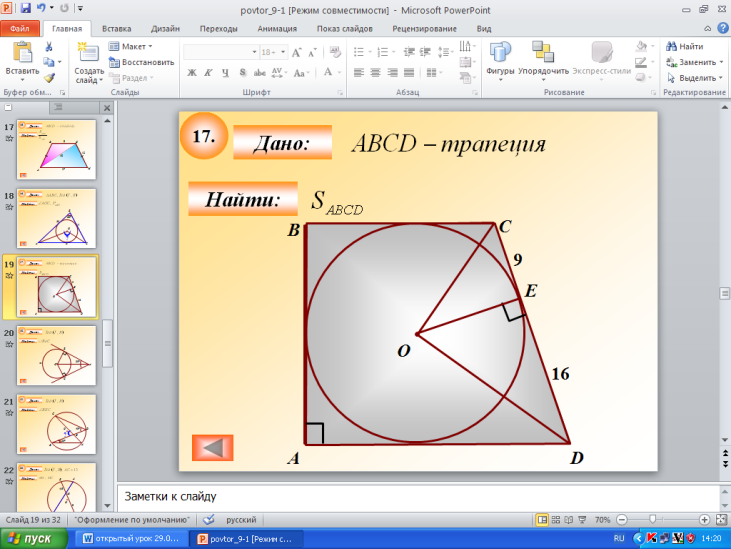
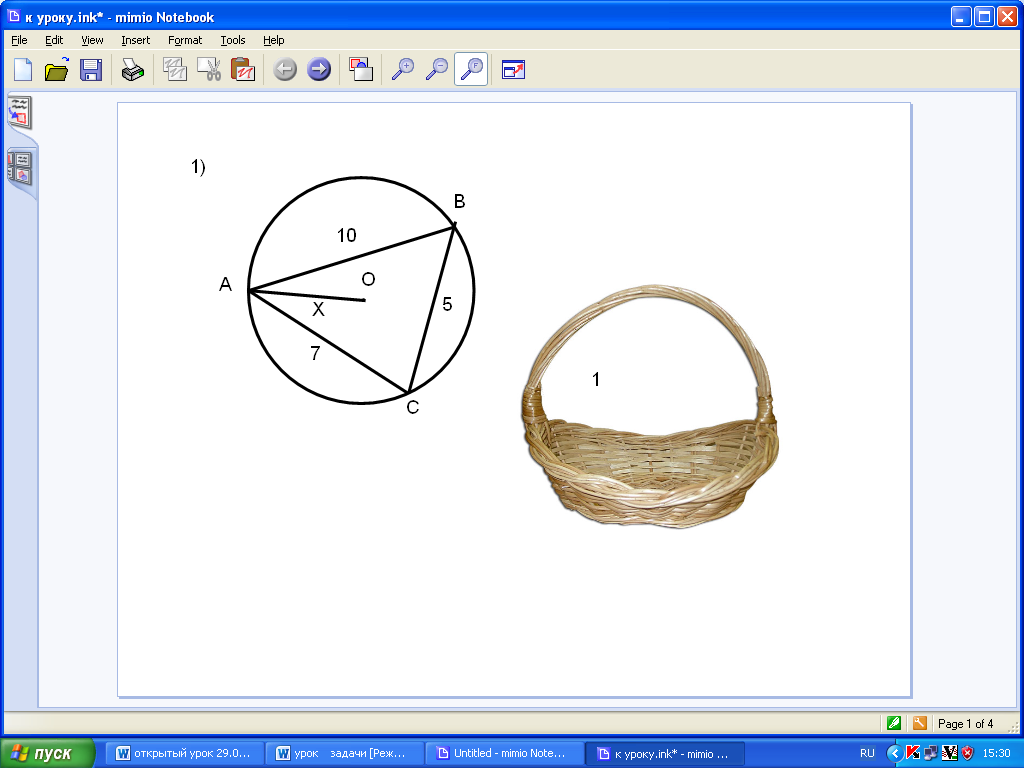
4. Комментарий к рисункам:Рисунок 3 Рисунок 4 Рисунок 5



Найти углы Найти площадь трапеции АВСD
четырёхугольника МРКN Найти периметр треугольника MBN,
если АВ=10, ВС=12, АС=6
5. Инструкция по выполнению работы
На рабочем столе найдите файл «Рисунки». Работаем вместе с классом
Выполнение теста на карточках, проверка через документ-камеру
Открыть Мимио-блокнот на нижней панели.
Работа в группах по заданию: для каждого из 5 рисунков выбрать из печатного списка теории только те утверждения, которые подходят по смыслу условия и предполагаемого решения задачи. Номера выбранных утверждений перенести в корзину, остальные оставить на месте. Работаем по проверке вместе с классом.
Решить каждую задачу в черновике, записать ответы в бланке (обратная сторона карточки самооценивания), сдать учителю
После проверки задач вместе с классом свернуть Мимио-блокнот.
Задачи к уроку: Гущин «Решу ГИА», № 311704 , № 311664
Открыть компьютер учителя на Рабочем столе. Работаем по тексту задачи вместе с классом над чертежом и условием.
Проверка чертежа через документ-камеру. Закончить решение с обоснованием.
Работа с компьютером учителя.
Проверка чертежа через документ-камеру
5. Контроль усвоения знаний. Текст: Биссектриса угла А треугольника АВС пересекает описанную около него окружность в точке D. Найти длину хорды DC, если центр окружности, вписанной в данный треугольник, удалён от точки D на расстояние m.
Текст: В треугольник с периметром, равным 20см, вписана окружность. Отрезок касательной, проведённой к окружности параллельно основанию, заключённый
между сторонами треугольника, содержит 2,4см. Найти основание треугольника.
Текст: Расстояния от центра окружности, вписанной в прямоугольный треугольник, до вершин его острых углов, равны √5см и √10см . Найдите катеты треугольника.
Критерии оценивания:
Задача №1 - «3», №10.372 Задача №2 - «4 , №10.369 Задача №3 - «5», №10.386
 Скачать 114.97 Kb.
Скачать 114.97 Kb.




