Обобщающий урок по теме

Название	Обобщающий урок по теме
Дата	28.02.2016
Размер	53.94 Kb.
Тип	Урок

Тема: Обобщающий урок по теме

«Функции и их графики»

Цель: Обобщить и систематизировать знания по теме «Линейная функция»; подготовить учащихся к контрольной работе; развивать грамотную математическую речь, умения анализировать и делать выводы; привить интерес к предмету.
Оборудование: рисунки с графиками; набор цифр 1,2,3,4 для каждого ученика.

Ход урока.

I. Оргмомент.

Знакомство с целью урока.

II. Устная работа.

Ответить на вопросы(Слайд 2):

Что называется функцией?
Как можно задать функцию?
Какие функции вам известны?
Что называется прямой пропорциональностью?
Что является графиком прямой пропорциональности?
От чего зависит расположение графика прямой пропорциональности?

Какую функцию называют линейной?
Что является графиком линейной функции?

III. Выполнение упражнений.

За каждый правильный ответ в таблице ставится « плюс».

Задание 1 (Слайд 3)

На рисунке изображены графики функций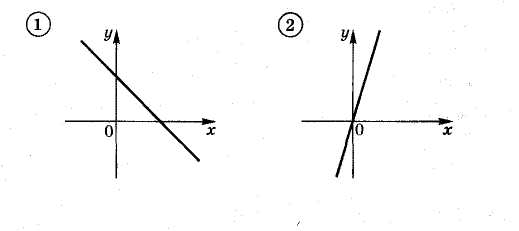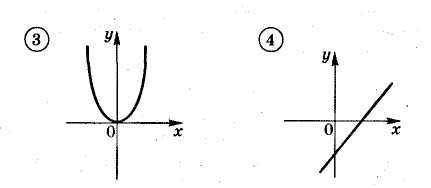

1. График какой функции мы не изучали? Ответ обоснуйте.

[3]

2. На каком рисунке изображен график прямой пропорциональности? Ответ обоснуйте.

[2]

3. На каком рисунке у графика линейной функции положительный угловой коэффициент? Ответ обоснуйте.

[4]

4. На каком рисунке у графика линейной функции отрицательный угловой коэффициент? Ответ обоснуйте.

[1]

Задание 2 (Слайд 4) Кто быстрее запишет?

Составьте самое длинное слово, связанное с темой нашего урока, из букв, которые записаны на доске: К, Ф, А, Д, И, О, Г, Р.

[График.]

Задание 3 (Слайд 5)

Даны функции 1) у =−3х; 2) у = 3х; 3) у = х – 3 и их графики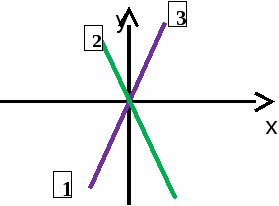

1. Под каким номером находится график функции у = – 3х? Ответ: 2

2. Под каким номером находится график функции у = 3х ? Ответ: 3

3. Под каким номером находится график функции у = х – 3 ? Ответ:1

Задание 4 (Слайд 6) При построении графиков ученик сделал ошибку. На каком из рисунков он сделал ошибку?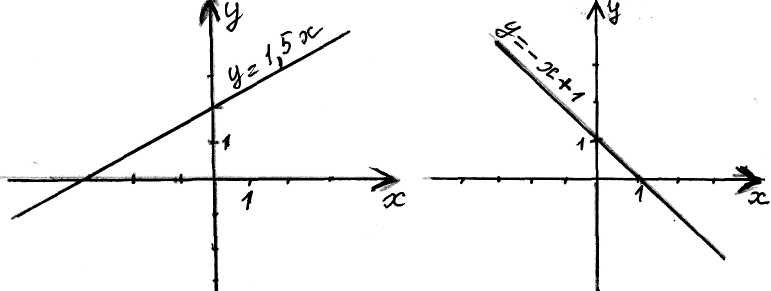

Задание 5 (слайд 7)

1. Постройте графики функций в одной системе координат:

у = 3; у = – 2,5х; у = х + 2.

1) В какой точке пересекает координатные оси график функции

у = х + 2? Назовите прямую пропорциональность, график которой параллелен графику функции у = х + 2.

2) Как расположен график функции у = 3?
Физкультминутка (слайд 8)

Задание 6 (слайд 9) Из предложенных формул, задающих линейную функцию, выберите ту, у которой угловой коэффициент к = – 3, а точка пересечения с осью ОУ

А(0; 7):

у = 3х +7; у = – 3х + 7; у = – 3х – 7

Задание 7 (слайд 10) Задайте формулой линейную функцию, если известен её угловой коэффициент и точка пересечения с осью ОУ:

к = – 2 А(0; 3) у = – 2х + 3

к = 7 А(0; – 13) у = 7х – 13
Задание 8 Самостоятельная работа в парах с последующей проверкой( на карточках)

Дана функция у = – 0,5х + 1. Какие из точек лежат на графике этой функции: 1) A(– 1; 0); 2) B(– 2; 2,5); 3) C(– 2; 0); 4) D(0; 1) ?
При каких значениях х значение функции у = – 0,5х + 1 равно 5?

1) х = 8; 2) х = – 8; 3) х = – 9

Даны функции:

1) у = – 2х – 1; у = – 2х – 3,5; у = – 2х + 5;

2) у = – 0,5х; у = 0,5х – 3; у = 1,5х + 5;

3) у =

х – 4; у =

х – 4; у = 3х – 4.

Графики каких функций: а) параллельны (объясните ответ);

б) пересекаются в одной точке.

Напишите функцию, график которой параллелен графику функции

у = – 8х + 1 и проходящей через начало координат.

Найдите координаты точки пересечения графиков функций:

у = 2х – 7 и у = – 3х + 8. Результат проверьте с помощью чертежа.

(один ученик график строит, а другой точку пересечения находит за закрытой доской) Ответ: (3; – 1)
IV. Подведение итогов.

Правильные ответы учеников в течение урока отмечаются «+» в таблице:

№ тура	Арсланова А.	Афанасьева А.	Бородина А.	Егорова Р.	Мустафина Э.	Слепцов В.	Чернов Л.
1
2
3
4
5
6
6
7
8
Всего «+»

V. Домашнее задание:

372(б, г), 329, 365