«Н. И. Лобачевский-создатель неевклидовой геометрии»
 Скачать 398.92 Kb. Скачать 398.92 Kb.
|
| Муниципальное бюджетное образовательное учреждение Уршельская средняя общеобразовательная школа Исследовательская работе по теме: «Н.И.Лобачевский-создатель неевклидовой геометрии» Научный руководитель: Зубенко Н.А. учитель математики Работу выполнила: Хмыляр Яна ученица 10 класса 2012 год ОГЛАВЛЕНИЕ Стр. Введение …………………………………………………. 3 Основная (содержательная часть) 1.Геометрия до Евклида………..………………………… 4-5 2. «Начала» Евклида…………………………………….... 6-7 2.1. V постулат Евклида…………………………………. 8-9 3. Создание неевклидовой геометрии……………………10-11 4. Лобачевский и его взгляды на геометрию……. …… 12 4.1. Биографическая справка …………………………... 12-13 4.2. Аксиоматика Гильберта………………………….. 14-18 4.3. Плоскость Лобачевского………. ………………… 19-22 4.4.Пространство Лобачевского………………………. 23-25 5.Вопрос о логической правильности неевклидовой геометрии………………………………………………. 26-28 6.Вклад Н.И. Лобачевского в развитие науки……………29 Заключение ………………………………………………. 30 Библиографический список……. …………………….. .31 Приложение (иллюстрации, таблицы)……………………32 ВВЕДЕНИЕ Любая теория современной науки считается единственно верной, пока не создана следующая. Это своеобразная аксиома развития науки. В течение двух тысяч лет геометрию узнавали либо из «Начал» Евклида, либо из учебников, написанных на основе этой книги. Лишь профессиональные математики обращались к трудам других великих греческих геометров: Архимеда, Аполлония и геометров более позднего времени. Классическую геометрию стали называть «евклидовой» в отличие от появившейся в ХIХ веке «неевклидовой геометрии». Об этом поразительном человеке история сохранила настолько мало сведений, что не редко высказываются сомнения в самом его существовании. Что же дошло до нас? Каковы пути развития геометрии как науки? В этой работе будет представлено историческое сравнение евклидовой геометрии с неевклидовой геометрией. В противовес евклидовой геометрии в работе представлен обзор труда Н.И.Лобачевского, поставившего вопрос об исследовании всей структуры системы аксиом, как евклидовой геометрии, так и других, возникших к этому времени. Цель работы – попытаться показать и раскрыть часть творчества выдающихся математиков Евклида и Лобачевского, кратко рассмотреть и сравнить основные положения наиболее известных их теорий, которые широко используются в настоящее время не только в образовании, но и нашли применение в области высоко точных технологий, инженерного проектирования в различных областях промышленного производства. 1.Геометрия до Евклида Геометрия – один из древнейших разделов математики. Наибольшего развития геометрических знаний достигли древневосточные цивилизации – Египет, Вавилон, Индия, Китай. Говорить о геометрии как науке на этой стадии нельзя – это была эпоха предварительного накопления геометрических сведений. В VII в. до н.э. благодаря торговле геометрические знания достигли Греции. Здесь геометрия получила широкое развитие, которое можно разделить на три периода: 1. (VII – VI в. до н. э.) Период является поворотным в развитии геометрии, основателем и представителем этого периода является Фалес Милетский. Греки впервые стали логически доказывать предложения геометрии в общем виде. Фалесу приписывают доказательство следующих теорем: — угол, вписанный в полуокружность, прямой. — вертикальные углы равны. — углы при основании равнобедренного треугольника равны между собой. и др. Это достижение греческих математиков имело важнейшее значение в развитии геометрии, т. к. общее доказательство охватывало все возможные частные случаи. Постепенно выделялись немногие первоначальные предложения, которые получены из опыта и должны быть положены в основу геометрии без логического доказательства. Было заложено начало созданию дедуктивного, или аксиоматического метода изложения геометрии. 2. (VI – V в. до н. э.) – олицетворяется Пифагором и его школой. Пифагору предписывают доказательство следующих предложений: — сумма внутренних углов треугольника равна двум прямым углам; — плоскость можно покрыть правильными треугольниками, четырехугольниками и шестиугольниками; — известная теорема Пифагора; — открытие геометрического способа решения квадратных уравнений; — открытие пяти правильных многогранников; Но самым важным открытием школы Пифагора явилось открытие несоизмеримых отрезков. До этого открытия греки считали, что отношение двух любых отрезков может быть выражено рациональным числом. Это явилось кризисом в развитии греческой математики, основное положение философии школы Пифагора, что «число есть мера вещей» потерпело поражение, а подняться до понятия иррационального числа они не сумели. Также разработка многих вопросов геометрии неизбежно приводила греческих математиков и философов к понятиям бесконечности и движения, к учению о бесконечно малых. К таким вопросам относились приближенные вычисления несоизмеримых величин, рассмотрение вопросов связанных со спрямлением окружности и квадратурой круга; вычисление объема поверхностей круглых тел и т. д. При этом греческие математики натолкнулись на глубокие противоречия и парадоксы, все это вызвало критику и споры среди философов. Нужно было сделать геометрию неуязвимой и при этом считалось, что это возможно лишь без привлечения понятий иррационального числа, бесконечности, движения. 3. (IV в. до н. э.) Философские школы в Афинах Платона и Аристотеля. С этими школами связывают два основных достижения: — выработку принципов научного построения геометрической системы, расчленение ее предложений на аксиомы, теоремы и определения; — разработку определенных методов и форм доказательства: анализ, синтез, доказательство от противного. Таким образом, до III в. до н. э. геометрия в Греции накопила обильный фактический материал, назрела необходимость в его систематизации. Эта задача наиболее полное и совершенное разрешение получила в созданных Евклидом «Началах». Начался новый период развития геометрии. 2. «Начала» Евклида Евклид (330-275 гг. до н. э.) – ученик школы Платона, при царе Птолемее I преподавал математику в Александрии – столице Древнего Египта. Из работ, написанных Евклидом, главным произведением являются «Начала». Эта книга намного превосходила более поздние труды математиков, она сыграла огромную роль в истории математики. Достаточно сказать, что она была переведена на все языки мира и выдержала около 500 изданий. До середины XIX века все математики учились по «Началам» Евклида. «Начала» Евклида состоят из 13 книг: I – VI посвящены планиметрии; VII – IX – арифметике; Х – несоизмеримым величинам; XI–XIII – стереометрии (XIII посвящена правильным многогранникам). Но не все из того, что уже было известно, изложено в «Началах», например, теория конических сечений в «Началах» не была представлена. Каждой из 13 книг «Начал» предпосылаются основные предложения, необходимые для вывода всех предложений рассматриваемой книги. Эти предложения делятся на 3 категории: определения, аксиомы и постулаты. Первая книга «Начал» начинается с 23-х определений. Приведём список некоторых определений «Начал»: 1. Точка есть то, что не имеет частей. 2. Линия есть длина без ширины. 3. Границы линии суть точки. . . . 23. Параллельные суть прямые, которые, находясь в одной плоскости и будучи продолжены в обе стороны неограниченно, ни с той ни с другой стороны между собой не встречаются. За определениями следуют постулаты и аксиомы, т. е. предложения, принимаемые без доказательства. Полный список аксиом и постулатов данный Евклидом не сохранился. Известно 5 постулатов и 10 аксиом. Постулаты: Требуется, 1. Чтобы из каждой точки ко всякой другой точке можно было провести прямую линию. 2. И чтобы каждую ограниченную прямую можно было продолжать неограниченно. 3. И чтобы из каждой точки, как из центра, можно было произвольным радиусом описать окружность. 4. И чтобы все прямые углы были равны друг другу. V постулат: 5. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше 2-х прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше 2-х прямых. Аксиомы: 1. Равные порознь третьему равны между собой. 2. И если к равным прибавим равные, то получим равные. . . . 6. И половины равных равны между собой. . . . 8. И целое больше части. 9. И две прямые не могут заключить пространства. С современной точки зрения, одно из слабых мест «Начал» Евклида – это определения. Он дает определения таких понятий как точка, плоскость, прямая, т. е. стремится дать определение всем геометрическим понятиям, а это невозможно. Многие его определения крайне туманны, например: 1. «Прямая есть линия, которая одинаково расположена относительно всех своих точек». 2. «Плоскость есть поверхность, которая одинаково расположена по отношению ко всем прямым, на ней лежащим». Евклид в «Началах» разделил постулаты и аксиомы. Но трудно провести между ними строгую грань. С современной точки зрения все они могут называться аксиомами. Другой важный недостаток «Начал» – неполнота системы аксиом: нет аксиомы непрерывности, аксиом движения и порядка, связанных с терминами «между» и «вне». Огромное историческое значение «Начал» Евклида в том, что они являются первым крупным научным документом по геометрии, в котором сделана попытка логического построения геометрии на основе аксиом. Чтобы закончить характеристику «Начал» Евклида необходимо остановиться на особо важном вопросе – о V постулате Евклида и попытках его доказательства. 2.1.V постулат Евклида «Начала» Евклида на протяжении более двух тысяч лет подвергались тщательному изучению. Имеется огромная литература, содержащая комментарии к «Началам». Уже древние комментаторы заметили, что «Начала» содержат существенные недостатки, в связи с этим предпринимались попытки их устранения. Особое внимание критиковавших «Начала» Евклида привлекал к себе V постулат. V постулат занимает в системе постулатов «Начал» особое положение в силу ряда глубоких соображений. Прежде всего, обращает на себя внимание то обстоятельство, что утверждение, содержащееся в V постулате, не имеет столь простого и очевидного характера, какой имеют прочие постулаты. Во-вторых, формулировка V постулата носит довольно сложный и громоздкий характер. И наконец, третья особенность заключается в весьма своеобразном использовании Евклидом этого постулата. В то время, как все остальные постулаты используются им с самого начала, при изложении первых теорем, V постулат применяется впервые лишь в доказательстве 29-го предложения. Таким образом, применение V постулата в «Началах» Евклида резко разграничивает геометрические предложения на две категории: на предложения, доказываемые без помощи V постулата; и на предложения, которые не могут быть доказаны без его использования. Предложения первой категории называются абсолютной геометрией, а второй – образует так называемую собственную евклидову геометрию. Изложенные особенности V постулата имели большое значение для последующего развития геометрии. Исследователи, жившие после Евклида, и комментаторы «Начал», рассматривали V постулат, как предложение, которое не следует помещать среди постулатов, а необходимо доказать как теорему. Они были убеждены в его доказуемости. Поэтому усилия многих поколений математиков были направлены на то, чтобы доказать V постулат при помощи остальных постулатов и тем самым свести его в разряд теорем. В этом и заключалась проблема V постулата Евклида. Решением этой проблемы занимались многие математики, в том числе: Посидоний (I в. до н. э.), Птолемей (III в. до н. э.), Прокл (410 – 475 гг), Насир-Эддин (1201 – 1274 гг.), Д. Валлис (1616 – 1703 гг.), Ламберт (1728 – 1777 гг.), Лежандр (1752 – 1833 гг.), Гаусс (1777 – 1855 гг.), И. Больяи (1802 – 1860 гг.). Все они неизменно оканчивались неудачей. Авторы доказательств в своих рассуждениях использовали явным или скрытым образом наглядно очевидные предложения, которые при тщательном анализе оказывались предложениями эквивалентными самому постулату. Например, наиболее интересная попытка доказательства была предпринята итальянским математиком Джироламо Саккери (1667 – 1733 гг.) – священник, профессор университета. Он пытался заменить V постулат Евклида его отрицанием и попытался вывести теорему, которая противоречила бы одной из доказанных Евклидом теорем. Полученное противоречие показало бы, что его предположение ложно и V постулат можно вывести из остальных. В процессе поиска он получил теорему, которая противоречила ранее полученным результатом, и написал книгу «Евклид, избавленный от всех пятен». Однако впоследствии математики выяснили, что Саккери в действительности не пришел к противоречию, и вопрос по-прежнему остается открытым. В середине XVIII в. над этой проблемой размышлял немецкий математик Ламберт. В отличие от Саккери, он понял, что любой набор гипотез, который не приводит к противоречию, порождает новую геометрию, и убедился, что V постулат Евклида невозможно вывести из остальных аксиом, т. е. аксиома о параллельных независима от остальных. Одно из доказательств V постулата, приведённое Проклом, можно посмотреть Здесь. Насколько велик труд, затраченный на исследования, связанные с проблемой доказательства V постулата, можно судить по тому, что известно около 250 серьёзных сочинений, посвящённых теории параллельности и не достигших поставленной цели. Однако, несмотря на безрезультатность и тщетность всех попыток доказательства V постулата, они всё же не были бесполезны. В результате этих многовековых поисков были выявлены логические зависимости между некоторыми важными геометрическими предложениями и, в частности, были открыты предложения, эквивалентные V постулату. Например, в современной школьной практике V постулат известен, как аксиома параллельных Плейфера: «Через точку, лежащую вне данной прямой, можно провести только одну прямую, параллельную данной». 3.Создание неевклидовой геометрии Безуспешные поиски доказательства 5-го постулата сыграли ту положительную роль, что помогли глубже проникнуть в структуру геометрии, уяснить взаимную связь её важнейших предложений. Эти попытки подготовили почву для возникновения у передовых учёных предположения, что 5-ый постулат недоказуем при помощи остальных аксиом геометрии Евклида. Здесь повторилось замечательное явление, неоднократно наблюдавшееся в истории науки вообще и математики в частности, когда достаточно созревшие новые идеи возникали у нескольких учёных одновременно. Это обстоятельство весьма красочно выражено в одном из писем Ф. Бояи к своему сыну Я. Бояи: «Как весной сразу всюду появляются фиалки, так и для научных открытий бывают эпохи, когда одни и те же мысли вспыхивают у учёных в разных местах». В течении первых же десятилетий XIX в. проблема 5-го постулата была решена несколькими лицами почти одновременно и независимо друг от друга, но совершенно не так, как предполагали это прежние учёные: была создана новая геометрия, независимая от 5-го постулата, основанная на замене его утверждением, эквивалентным гипотезе острого угла Саккери. К открытию новой, так называемой «неевклидовой», геометрии пришли три человека: 1) профессор Казанского университета Николай Иванович Лобачевский (1792–1856); 2) великий немецкий математик Карл Фридрих Гаусс (1777–1855); 3) венгерский офицер Янош Бояи (1802–1860). Однако вклад в создание новой геометрии, сделанный этими учёными, весьма неравноценен. Что касается Гаусса, то он совершенно не оставил никаких следов систематического изложения своих открытий в области неевклидовой геометрии и при жизни не опубликовал ни одной строчки по этому вопросу. Гаусс слишком боялся уронить свой огромный авторитет в глазах учёного мира. Янош Бояи пришёл к открытию неевклидовой геометрии в 1823 г., будучи в возрасте 21 года, но опубликовал свои результаты в 1832 г. (позже Лобачевского) в виде приложения к учебнику математики «Опыт введения учащегося юношества в начала чистой математики», изданному его отцом Ф. Бояи. Но, непонятый своими современниками, встретивший сдержанное, нечуткое отношение со стороны Гаусса, он впал в глубокое отчаяние. Больше ни одного произведения по новой геометрии Я. Бояи не опубликовал. Остаток жизни он трагически провёл в нужде, неизвестности и полном одиночестве, пережив и Гаусса, и Лобачевского. Однако всё сделанное в области геометрии Гауссом и Я. Бояи представляет собой лишь первые шаги по сравнению с глубокими и далеко идущими исследованиями Лобачевского, который всю жизнь упорно и настойчиво разрабатывал с разных точек зрения своё учение, довёл его до высокой степени совершенства и опубликовал целый ряд крупных сочинений по новой геометрии. Поэтому как с формальной стороны (первое по времени опубликование открытия в 1826 г.), так и по существу первое место среди лиц, разделяющих славу создания неевклидовой геометрии, следует безраздельно отвести Н. И. Лобачевскому, имя которого и носит созданная им геометрия. Следует указать ещё на двух лиц, пришедших к идеям новой геометрии: 1) Ф. К. Швейкарт (1780–1859), профессор права в Харьковском университете с 1812 по 1817 г. и 2) его племянник Тауринус (1794–1874). Однако они дали лишь самые беглые наброски новой геометрии. Геометрия Лобачевского так и не была понята и оценена при жизни самого учёного. Но уже через десятилетие после смерти Лобачевского его открытие привлекло всеобщее внимание математических кругов и послужило могучим стимулом к коренному пересмотру взглядов на основания геометрии. Это объясняется тем, что к этому времени самим развитием математики была подготовлена почва к правильному восприятию и пониманию идей Лобачевского и к их дальнейшему углублению и развитию. 4. Лобачевский и его взгляды на геометрию 4.1. Биографическая справка Лобачевский Николай Иванович родился: 01.12.1792, в Нижнем Новгороде. Умер: 24.02.1856, в Казани. Ему поставлен памятник, поэт В. Фирсов написал на нем:  Рисунок 1. «Н.И.Лобачевский» Высокий лоб, нахмуренные брови В холодной бронзе – отраженный луг… Но даже неподвижный и суровый, Он как живой, - спокоен и могуч. Когда-то здесь, на площади широкой, Задумчивый, неторопливый, строгий, Он шел на лекции – великий и живой. Пусть новых линий не начертят руки, Он здесь стоит, взнесенный высоко, Как утверждение бессмертья своего, Как вечный символ творчества науки. Детство Лобачевского было тяжелым и бедным. В Казанской гимназии он был казеннокоштным студентом, что накладыавало определенные обязанности и ограничения. Самым простым было учиться лучше других. Но уже с самого начала жизни Лобачевский интересовался геометрией. Это неудивительно, ведь его отец был землемером. Лобачевский проявил также большую склонность к языкам – например, французский он выучил за три месяца. Он писал стихи – его поэмы о Волге считаются одними из лучших. Но при этом он не забывал учиться – в 1807 году он студент, а в 1811 – магистр. В 1811 году окончил Казанский университет и был оставлен при нем для подготовки к профессорскому званию. В 1814-46 году преподавал в этом университете (с 1816 года - профессор, заведовал астрономический обсерваторией университета, в 1820-22, 1823-25 – декан физико-математического факультета, в 1827-46 – ректор). С 1846 - помощник попечителя Казанского учебного округа. Лобачевский оказал влияние на развитие астрономии. Лобачевский является создателем новой геометрической системы - неевклидовой геометрии, или геометрии Лобачевского, изложенной в его труде «О началах геометрии» (1829). Первым попытался использовать данные астрономических наблюдений (параллаксы звезд) для определения свойств пространства и времени и решения вопроса о том, какая из двух геометрий – классическая евклидова или созданная им – соответствует реальным условиям в физическом пространстве. Однако имевшиеся в его распоряжении величины параллаксов, опубликованные французским астрономом – любителем Дасса – Мондидье, были весьма завышенными и далекими от реальности. Лобачевский пришел к выводу, что в пределах пространства, ограниченного расстояниями до ближайших звезд, различие в обеих геометриях настолько мало, что выявить его методами того времени невозможно. Вопрос о геометрии физического пространства, впервые поставленный Лобачевским, был решен в теории относительности, созданной в xx в. А.Энштейном: геометрия Вселенной определяется распределением вещества в ней и не является евклидовой. В 1895 году Казанское физико-математическое общество учредило премию имени Лобачевского за выдающиеся работы в области геометрии. В настоящее время эту премию присуждает АН СССР. 4.2. Аксиоматика Гильберта Геометрия Лобачевского выдвинула ряд важнейших проблем в области учения об аксиомах геометрии. Во-первых, геометрия Лобачевского, явившись первым доказательством независимости аксиомы параллельных от прочих аксиом Евклида, выдвинула общий вопрос об исследовании независимости аксиом геометрии. Вместе с тем выяснилось, что этот вопрос упирается в неполноту системы аксиом «Начал» Евклида, выяснилась необходимость разработки перечня всех необходимых и достаточных предпосылок геометрии. Наконец возникли две тесно связанные проблемы, порождённые тем обстоятельством, что сам Лобачевский не довёл до конца исследование о непротиворечивости своей системы и о реальном её осуществлении. При этом следует отметить, что Лобачевский созданием своей геометрии не только поставил эти проблемы в области обоснования геометрии, но и предуказал пути для их решения. Своими идеями Лобачевский оказал огромное влияние на исследования западноевропейских математиков второй половины XIX столетия, определив направление и тематику многих выдающихся работ этого периода, приведших к развитию современного аксиоматического метода в математике и созданию новых «неевклидовых» геометрий. Настойчивая и углублённая работа над созданием прочного логического фундамента геометрии получила своё наиболее полное завершение в вышедшей в 1899 г. знаменитой работе выдающегося немецкого математика Давида Гильберта – «Основания геометрии». Являясь известным завершением работ Лобачевского в области исследований взаимной независимости аксиом геометрии, книга Гильберта содержит важнейшие идеи по аксиоматическому обоснованию геометрии, явившиеся исходным пунктом дальнейших изысканий как в области геометрии, так и в области других математических наук. Работа Гильберта в основном разрешила вопрос о построении полной аксиоматики геометрии. В ней изложена первая полная система аксиом Евклида. Аксиомы Гильберта делятся на 5 групп. I. Аксиомы связи (соединения, сочетания): 1) Для любых двух точек A и B существует прямая, принадлежащая каждой из них. 2) Существует не более одной прямой, принадлежащей каждой из двух данных точек A и B. 3) На каждой прямой существуют по крайней мере две точки. Существуют по меньшей мере три точки, не принадлежащие одной прямой II.Аксиомы порядка или расположения: 1) Если точка B лежит между точкой A и точкой C, то A, B, C – различные точки одной прямой и B лежит также между C и A. 2) Если A и B – две точки, то на прямой AB всегда существует по меньшей мере одна такая точка C, что B лежит между A и C. 3) Из трёх точек прямой не более одной точки лежит между двумя другими. Определение. Систему двух точек A и B на прямой a называется отрезком AB или BA. Точки, лежащие между A и B, называются точками отрезка AB, а сами точки A и B – концы отрезка. 4) (Аксиома Паша). Пусть A, B, C – три точки, не лежащие на одной прямой, и a - прямая в плоскости ABC, не проходящая ни через одну из точек A, B, C. Тогда если прямая a проходит через внутреннюю точку отрезка AB, то она проходит также через внутреннюю точку одного и только одного из двух других отрезков AC или BC. 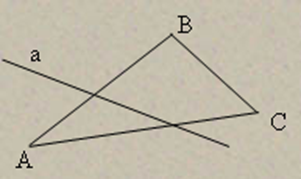 Рисунок 2. "Аксиома Паша" III.Аксиомы конгруэнтности: 1) Если A и B – две точки прямой a и A' – точка на той же или другой прямой a', то существует на прямой a' по данную сторону от точки A' такая точка B', что отрезок AB конгруэнтен отрезку A'B', что обозначается знаком AB≡A'B'. Всегда AB≡BA. 2) Если AB≡A'B' и AB≡A''B'', то A'B'≡A''B''. 3) Пусть AB и BC – два отрезка прямой a без общих внутренних точек и пусть A'B' и B'C' – два отрезка прямой a' (отличной от a или с ней совпадающей) также без общих внутренних точек. Если AB≡A'B', BC≡B'C', то AC≡A'C'. 4) Пусть дан ے(h,k) в плоскости α, а также определённая относительно прямой a' полуплоскость плоскости α', пусть h' – луч прямой a', выходящий из точки O'. Тогда на плоскости α' существует один и только один луч k', такой, что ے(h,k) конгруэнтен ے(h',k') и при этом все внутренние точки ے(h',k') лежат в данной полуплоскости α', это записывается символически: ے(h,k)≡ے(h',k'). Всегда ے(h,k)≡ے(h,k) и ے(h,k)≡ے(k,h). 5) Если для двух треугольников ABC и A'B'C' имеют место конгруэнции: AB≡A'B', AC≡A'C', ےBAC≡ےB'A'C', то ےABC≡ےA'B'C' Если множество всех точек пространства поставлено во взаимно однозначное соответствие с множеством всех точек того же пространства, то будем называть такое точечное соответствие преобразованием или отображением пространства в самого себя. Движением называется такое преобразование пространства в самого себя, при котором всякий отрезок преобразуется в конгруэнтный отрезок. С другой стороны, две фигуры называются конгруэнтными, если существует такое движение, которое преобразует первую фигуру во вторую. Таким образом, мы можем резюмировать связь между понятиями конгруэнтности и движения следующим образом: при наличии аксиом Гильберта I-II аксиомы конгруэнтности Гильберта III и аксиомы движения III' являются эквивалентными. III'.Аксиомы движения: 1) Каждую точку пространства движение преобразует в точку того же пространства. 2) Если прямая a и лежащая на ней точка A движением преобразуются в прямую a' и точку A', то точка A' лежит на прямой a'. Последовательное применение двух преобразований называется произведением этих преобразований. 3) Совокупность всех движений образует группу, то есть: а) Произведение двух движений есть также движение. б) Существует движение, при котором каждая точка преобразуется сама в себя. Такое движение называется тождественным и играет роль единицы группы движений. в) Для каждого движения существует обратное движение, произведение которого с данным движением даёт тождественное движение. г) Произведение движений ассоциативно, то есть удовлетворяет сочетательному закону. 4) Если три точки A, B, C, из которых B лежит между A и C, при движении преобразуются в точки A', B', C', то B' лежит между A' и C'. 5) Существует одно и только одно движение, преобразующее данную точку A, определённый луч с вершиной в A и определённую полуплоскость относительно этого луча соответственно в другую данную точку A', в определённый луч с вершиной в A' и в определённую полуплоскость относительно этого луча. 6) Существует движение, при котором отрезок AB переходит в отрезок BA. 7) Существует движение, при котором ے(h,k) переходит в ے(k,h). 8) Если точка O и исходящий из неё луч преобразуются движением в самих себя, то каждая точка этого луча преобразуется сама в себя. IV. Аксиома непрерывности: Первый, кто дал точную формулировку сущности понятия непрерывности, был Дедкинд (1831-1916). Аксиома Дедекинда формулируется так: Если все точки отрезка AB, включая и его концы, распределены на два класса так, что: 1) каждая точка отрезка принадлежит одному и только одному из этих классов, точка A принадлежит первому классу, а точка B – второму классу; 2) каждая точка первого класса, отличная от A, лежит между A и любой точкой второго класса, то на отрезке AB существует одна и только одна такая точка C, что всякая точка, лежащая между A и C, принадлежит первому классу, а всякая точка, лежащая меду C и B, принадлежит второму классу. Сама точка C принадлежит либо первому, либо второму классу.  Рисунок 3."Аксиома Дедекинда" В своей системе не пользуется аксиомой Дедекинда, а вместо неё вводит две аксиомы – аксиому Архимеда и так называемую аксиому полноты, которые в своей совокупности эквивалентны аксиоме Дедекинда относительно аксиом I – III групп. IV1.(Постулат Архимеда.) Пусть AB и CD – два произвольных отрезка и пусть на луче AB с вершиной A взяты точки A1, A2, A3,…, расположенные так, что A1 лежит между A и A2, точка A2 лежит между A1 и A3 и т. д., причём отрезки AA1, A1A2, A2A3,… конгруэнтны отрезку CD. Тогда существует такой номер n, что точка B лежит между A и An.  Рисунок 4. "Постулат Архимеда" IV2.(Принцип вложенных отрезков Кантора.) Пусть на произвольной прямой a дана бесконечная последовательность отрезков A1B1, A2B2, A3B3,…, из которых каждый последующий лежит внутри предыдущего, пусть при этом не существует отрезка, лежащего внутри всех отрезков данной последовательности. Тогда на прямой a существует одна и только одна точка M, лежащая внутри всех отрезков A1B1, A2B2, A3B3,… 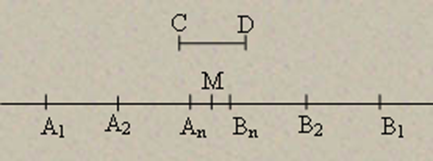 Рисунок 5. "Принцип вложенных отрезков Кантора" V. Аксиома параллельности: Все те предложения геометрии, которые могут быть доказаны на основе аксиом соединения, порядка, конгруэнтности и непрерывности, составляют абсолютную геометрию. В зависимости от того, примем ли мы в качестве дополнительного требования, что бы указанная прямая была единственной или нет, мы получим соответственно либо геометрию Евклида, либо геометрию Лобачевского. Аксиому параллельности евклидовой геометрии можно сформулировать так: Пусть a - произвольная прямая и A – точка, лежащая вне прямой; тогда в плоскости, определяемой ими, через точку A можно провести не более одной прямой, не пересекающей a. Эта формулировка принадлежит Плейферу. Если мы в аксиоме V вместо слов «не более одной прямой» поставим слова «более одной прямой», то мы получим аксиому Лобачевского, и тогда система аксиом I – V будет определять геометрию Лобачевского. Аксиома о параллельности Лобачевского: Пусть a - произвольная прямая и A – точка, лежащая вне прямой; тогда в плоскости, определяемой ими, через точку A можно провести более одной прямой, не пересекающей a. 4.3.Плоскость Лобачевского Исходным пунктом геометрии Лобачевского является принятие всех предложений геометрии Евклида, не зависящих от 5-го постулата (то есть абсолютной геометрии, включая аксиомы Паша, Архимеда, Дедекинда), и присоединение к ним взамен отброшенного 5-го постулата следующей аксиомы, противоположной аксиоме Плейфера, а значит, и 5-му постулату. Через точку, лежащую вне прямой в плоскости, определяемой ими, можно провести не менее двух прямых, не пересекающих данной прямой. Заметим, что существование хотя бы одной прямой, проходящей через данную точку и не пересекающей данной прямой, есть факт абсолютной геометрии. Аксиома Лобачевского утверждает существование по крайней мере двух таких прямых. Отсюда немедленно следует, что таких прямых существует бесконечное множество. Плоскость, в которой предполагается выполнение аксиомы Лобачевского, называется плоскостью Лобачевского. Заметим также, что геометрию Лобачевского называют гиперболической геометрией, в соответствии с чем плоскость и пространство Лобачевского называются гиперболическими. Основная теорема. Пусть в плоскости даны прямая a и не лежащая на ней точка A. Тогда в пучке прямых с центром в точке A существуют две пограничные прямые, разделяющие все прямые пучка на два класса: на класс прямых, пересекающих a, и класс прямых, не пересекающих a. Эти граничные прямые сами не пересекают a. 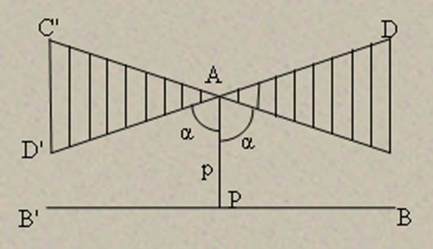 Рисунок 6. "Основная теорема Лобачевского" Всё сказанное приводит нас к следующей картине расположения прямых пучка с центром в точке A, взятой вне данной прямой BB'. В этом пучке существуют две граничные прямые CC' и DD' (рис.7), симметрично расположенные относительно перпендикуляра AP, опущенного из точки A на BB', и образующие с ним ےCAP=ےD'AP=α< . Эти прямые, а также все прямые пучка, проходящие внутри заштрихованных вертикальных углов CAD и C'AD', не пересекают прямой BB', а все прямые пучка, проходящие внутри вертикальных углов CAD' и C'AD, пересекают BB'. Две граничные прямые CC' и DD' называются параллельными прямой BB' в точке A, причём прямая C'C называется параллельной B'B в направлении B'B, а прямая DD' называется параллельной прямой BB' в направлении BB'. Острый угол α, образуемый параллельными с перпендикуляром AP, называется углом параллельности в точке A относительно прямой BB'. Этот угол есть функция длины p перпендикуляра AP и обозначается так: α=П(p). AP называется отрезком параллельности в точке A относительно прямой BB'. Основная формула геометрии Лобачевского, устанавливающая зависимость между длиной отрезка и отвечающим ему углом параллельности, имеет вид: Все прямые пучка, не пересекающие BB' и лежащие внутри заштрихованных вертикальных углов, называются расходящимися с BB' или сверхпараллельными к BB'; угол, образуемый такой прямой с перпендикуляром AP с обеих от него сторон, больше угла параллельности α. Наконец, все остальные прямые пучка, образующие с AP с какой-либо стороны острый угол, меньший угла параллельности α, называются пересекающими прямую BB' или сходящимися с BB'. Определение. Прямая C'C называется параллельной прямой B'B в направлении B'B (рис.8) в точке A, если, во-первых, прямая C'C не пересекает прямой BB', во-вторых, C'C является граничной в пучке прямых с центром в точке A, то есть всякий луч AE, проходящий внутри угла CAD, где D – любая точка прямой BB', пересекающей луч DB. 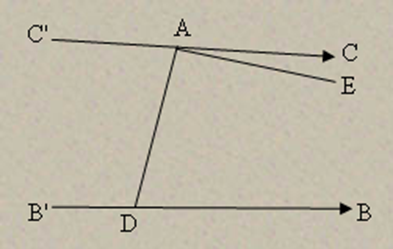 Рисунок 7. "Параллельность прямой в плоскости" Замечание. Из вышеизложенного ясно, что через точку A, лежащую вне прямой BB', можно провести в каждом из двух направлений лишь единственную параллельную Лобачевского к прямой BB', то есть каждому значению длины перпендикуляра p соответствует вполне определённое значение угла параллельности α. В плоскости Лобачевского две прямые могут либо пересекаться, либо могут быть параллельными в некотором направлении, либо расходящимися. Поэтому в плоскости Лобачевского существует три вида пучков прямых: 1) пучок прямых, пересекающихся в одной точке, называемой центром пучка; такой пучок называется центральным или эллиптическим; 2) пучок прямых, параллельных в заданном направлении некоторой прямой, называемой осью пучка; такой пучок называется параболическим; 3) пучок расходящихся прямых, перпендикулярных к некоторой прямой, называемой базой пучка; такой пучок называется гиперболическим. Легко убедиться, что любой из этих пучков определяется двумя своими прямыми, а параболический – одной с выбранным на ней направлением и что через всякую точку плоскости (кроме центра эллиптического пучка) проходит одна и только одна прямая пучка. Эти три вида пучков связаны с тремя основными кривыми плоскости Лобачевского, являющимися кривыми постоянной кривизны. Для дальнейшего развития учения о пучках и о кривых постоянной кривизны нам придётся ещё рассмотреть так называемые секущие равного наклона. Определение. Секущей равного наклона к двум данным прямым называется прямая, которая при пересечении с данными образует равные внутренние односторонние углы. Введём понятие о точках, соответственных относительно пучка. Определение. Если a и b – две прямые пучка и AB – какая-нибудь секущая равного наклона, пересекающая a и b в точках A и B, то эти точки называются взаимно соответственными относительно пучка. Возьмём какую-нибудь прямую a данного пучка и на ней произвольную точку A. Тогда, проводя через точку A секущие равного наклона ко всем прямым пучка, мы на каждой прямой пучка найдём точку, соответственную точке A относительно пучка. Геометрическое место всех таких точек определит на плоскости некоторую линию. В зависимости от того, какого рода пучок рассматриваем, мы получим различные линии, построенные указанным выше способом. Определение. Геометрическое место точек, соответственных некоторой точке A, взятой на одной прямой пучка, называется окружностью, орициклом (или, иначе, предельной линией) или эквидистантой в зависимости от того, будет ли данный пучок прямых соответственно эллиптическим, параболическим или гиперболическим. Сама точка A также включается в соответствующее геометрическое место. Заметим, что прямая, как база гиперболического пучка, является частным случаем эквидистанты. Орицикл может скользить по себе самому без деформации, подобно тому как это имеет место для прямой и окружности. Таким же свойством обладает и эквидистанта: если заставить скользить по самой себе базу эквидистанты, то и сама эквидистанта будет скользить сама по себе без деформации, ибо расстояния всех точек эквидистанты от базы равны между собой. Таким образом, в геометрии Лобачевского имеется четыре типа линий постоянной кривизны: прямая, окружность, орицикл и эквидистанта. В зависимости от того, принадлежат ли три перпендикуляра в серединах сторон треугольника к эллиптическому, гиперболическому или параболическому пучку, около треугольника можно описать либо окружность, либо эквидистанту, либо орицикл, ибо стороны треугольника будут секущими равного наклона относительно соответствующего пучка. В отличие от окружности орицикл и эквидистанта – линии незамкнутые. 4.4.Пространство Лобачевского Пространство, в которой предполагается выполнение аксиомы Лобачевского, называется пространством Лобачевского. В пространстве Лобачевского параллельность и расходимость прямых, а также прямой и плоскости, определяется следующим образом: Определение. Две прямые в пространстве называются параллельными (расходящимися), если они лежат в одной плоскости и в этой плоскости они параллельны (расходятся). Определение. Прямая a называется параллельной плоскости α, если она параллельна своей проекции на эту плоскость. Определение. Прямая a называется расходящейся с плоскостью α, если она расходится со своей проекцией на эту плоскость. Из последних определений немедленно следует, что прямая, параллельная плоскости, неограниченно сближается с последней в сторону параллельности, а прямая, расходящаяся с плоскостью, имеет с этой плоскостью единственный общий перпендикуляр, в обе стороны от которого в проектирующей плоскости прямая неограниченно удаляется от плоскости. Взаимное расположение прямых и плоскостей в пространстве Лобачевского вполне характеризуется при помощи так называемого конуса параллельности, являющегося аналогом понятия угла параллельности.  Рисунок 8. "Расположение прямых и плоскости в пространстве" Пусть дана плоскость α и не лежащая на ней точка A (рис. 9). Пусть AA' – перпендикуляр к α, проектирующий точку A в точку A' на плоскости α. Пусть далее AB – прямая, параллельная плоскости α, и A'B' – её проекция на α. Тогда угол BAA' есть угол параллельности в точке A прямой AB относительно прямой A'B'. Будем вращать прямую AB около перпендикуляра AA', тогда AB опишет круглую коническую поверхность с вершиной в точке A, все образующие которой параллельны плоскости α. Эта поверхность называется конусом параллельности в точке A относительно плоскости α. Таким образом, конусом параллельности в точке A относительно плоскости α называется геометрическое место всевозможных прямых, параллельных плоскости α в точке A. Из этого определения ясно, что всякая прямая, проходящая через точку A и лежащая внутри конуса параллельности, пересекает плоскость α, а всякая прямая, проходящая через точку A и лежащая вне конуса параллельности, расходится с плоскостью α. Конус параллельности в точке A позволяет все плоскости, проходящие через точку A, разбить на три категории: 1) плоскости, пересекающие конус по двум образующим, 2) плоскости, касающиеся конуса по образующей, 3) плоскости, имеющие с конусом лишь одну общую точку A. Плоскости 1-й категории содержат прямые, проходящие через A и лежащие внутри конуса параллельности, а потому эти плоскости пересекают плоскость α. При этом прямая пересечения с плоскостью α параллельна в противоположных направлениях проекциям образующих, по которым плоскость 1-й категории пересекает конус параллельности. Плоскости 2-й и 3-й категории не содержат прямых, проходящих внутри конуса параллельности, а потому не могут пересекаться с плоскостью α. Определение. Плоскость, проходящая через точку A, называется сходящейся с плоскостью α, параллельной плоскости α, или расходящейся с плоскостью α, смотря по тому, будет ли эта плоскость пересекать конус параллельности в точке A по паре образующих, или будет касаться конуса по образующей, или не будет иметь с конусом общих прямых. В плоскости Лобачевского через точку, лежащую вне прямой, проходят две прямые, параллельные данной. В пространстве Лобачевского через точку, лежащую вне плоскости, можно провести бесконечное множество прямых, параллельных данной плоскости, это и будут образующие конуса параллельности. В пространстве Лобачевского существует четыре типа поверхностей, которые могут без деформации передвигаться сами по себе, так, чтобы каждая точка поверхности совмещалась с любой другой её точкой и притом, чтобы направление любой касательной к поверхности в первой точке совместилось с направлением любой касательной во второй точке. Эти поверхности являются аналогами прямой, окружности, орицикла и эквидистанты на плоскости. Построение этих поверхностей может быть проведено по тому же плану, что и построение основных кривых на плоскости. Для этого воспользуемся понятием связки прямых. Определение. Связкой прямых называется совокупность всех таких прямых в пространстве, каждая пара которых лежит в одной плоскости. Эти плоскости называются плоскостями связки. Из этого определения вытекает, что в пространстве Лобачевского существует лишь три типа связок в соответствии с тремя возможностями взаимного расположения пары прямых в плоскости Лобачевского. Действительно, пусть a и b – две прямые связки. Так как они по определению лежат в одной плоскости, то возможны три случая: 1) либо a и b пересекаются в некоторой точке O (такая связка называется эллиптической), 2) либо они параллельны (такая связка называется параболической), 3) либо они расходятся (такая связка называется гиперболической). Введём понятие о соответственных точках. Определение. Если a и b – две прямые связки и AB – секущая равного наклона, пересекающая a и b в точках A и B, то эти точки называются взаимно соответственными относительно связки. Взяв в данной связке некоторую прямую a и на ней произвольную точку A, будем из этой точки проводить секущие равного наклона к прямой a со всеми прямыми связки. Таким путём мы получим все соответственные с A точки относительно данной связки. Определение. В зависимости от того, будет ли данная связка эллиптической, параболической или гиперболической, геометрическое место точек, соответственных с A относительно связки, называется сферой, орисферой или эквидистантной поверхностью. Сама точка A также включается в соответствующую поверхность. Плоскость является частным случаем эквидистантной поверхности. Любая из этих поверхностей определяется заданием двух прямых, лежащих в одной плоскости, и точки на одной из них, а орисфера определяется заданием только одной прямой с выбранным на ней направлением и точкой на ней. Эта прямая называется осью орисферы. Плоскость связки пересекает сферу по окружности, орисферу – по орициклу, эквидистантную поверхность – по эквидистанте. Любая плоскость связки называется диаметральной плоскостью соответствующей поверхности. Замечательным является тот факт, что орициклам на орисфере можно приписать ту же роль, что и прямым на плоскости. Оказывается, что орициклы на орифере удовлетворяют всем аксиомам абсолютной геометрии, каким удовлетворяют прямые на плоскости. 5.Вопрос о логической правильности неевклидовой геометрии До начала XIX столетия ни одна из попыток доказательства V постулата не увенчалась успехом. Таким образом, проблема V постулата оставалась неразрешимой. И только в начале XIX в. были получены результаты, которые привели к решению этой проблемы. Основная заслуга в этом принадлежит знаменитому русскому учёному Н. И. Лобачевскому. В течение первых лет преподавательской деятельности в Казанском университете Н. И. Лобачевский настойчиво пытался доказать V постулат. Неудачи этих попыток и попыток его предшественников привели к выводу, что V постулат не может быть выведен из остальных постулатов геометрии. Чтобы это доказать, Н. И. Лобачевский построил логическую систему, в которой, сохраняя основные посылки Евклида, он отвергает V постулат и заменяет его противоположным допущением. Он пришёл к выводу, что эта логическая схема представляет собой новую геометрию, которая может быть развита так же успешно, как и геометрия Евклида. 23 февраля 1826 г. Н. И. Лобачевский представил физико-математическому факультету Казанского университета доклад по теории параллельных под названием «Рассуждения о принципах геометрии». В 1829 г. в «Учёных записках Казанского университета» он поместил статью «О началах геометрии». Это была первая опубликованная работа по новой геометрии. В последующие годы Лобачевский издал ещё ряд сочинений по геометрии. В этих сочинениях он первым отчётливо сформулировал и обосновал утверждение о том, что V постулат Евклида нельзя вывести из остальных аксиом геометрии. Лобачевский развивает свою геометрию на плоскости и в пространстве до тех же пределов, до каких была развита Евклидова геометрия, включая и формулы тригонометрии. Эту новую геометрию он назвал «воображаемой» (впоследствии её стали называть геометрией Лобачевского или гиперболической геометрией). Открывая всё новые и новые факты, Лобачевский не встретил в своей геометрии каких-либо логических противоречий. Исследования, проделанные им, привели к убеждению, что его логическая схема свободна от логических противоречий. Желая показать, что его геометрия никогда не приведёт к противоречию, Лобачевский даёт её аналитическое исследование и решает проблему непротиворечивости своей геометрии вполне удовлетворительно для того времени. Приведём статью Кагана, в которой описаны первые попытки доказать непротиворечивость геометрии Лобачевского, предпринятые самими создателями этой геометрии. "Когда неевклидова геометрия была развернута, по крайней мере, в элементарных своих частях, перед ее творцами встал вопрос о логической ее правильности, о ее «непротиворечивости», как теперь говорят. Вопрос состоял в том, существует ли полная уверенность, что никакое дальнейшее ее развитие не может привести к противоречию. Не подлежит никакому сомнению, что и Лобачевский и Бояи много об этом размышляли и искали в пользу этого такие доводы, которые не могли бы вызвать никаких возражений. В записях, сохранившихся после смерти Бояи, Штекель обнаружил утверждение о том, что он нашел точное доказательство логической правильности построенной им геометрии и что он намерен это доказательство изложить. Однако никаких следов такого доказательства, хотя бы руководящей его идеи, в наследии Бояи не сохранилось. Нужно сказать, что сама заметка эта относится к последним годам жизни Бояи, когда он уже утратил ясность и точность мысли. Вряд ли может подлежать сомнению, что вера в найденное им доказательство была иллюзией. Лобачевский размышлял над этим вопросом всю жизнь, и в каждой из своих работ приводит соображения, которые объективно убеждают его в безупречной правильности «воображаемой» геометрии. Мемуар «О началах геометрии» заканчивается следующем образом: «После того, как мы нашли уравнения которые представляют зависимость углов и боков треугольников, когда, наконец, дали мы общие выражения для элементов линий, площадей и объема тел, все прочее в Геометрии будет уже аналитикой, где исчисления необходимо должны быть согласны между собою и ничего не в состоянии открыть нам нового, чего бы не заключалось в тех первых уравнениях, откуда должны быть взяты все отношения геометрических величин друг к другу. Итак, если надобно предполагать теперь, что какое-нибудь противоречие принудит впоследствии опровергнуть начала, принятые нами в этой новой геометрии, то это противоречие может только скрываться в самих уравнениях (1). Заметим, однакож, что эти уравнения переменяются в уравнения сферической Тригонометрии, как скоро вместо боков a, b, c ставим но в обыкновенной Геометрии и сферической Тригонометрии везде входят одни содержания линий: следовательно, обыкновенная Геометрия, Тригонометрия и эта новая Геометрия всегда будут согласны между собой». Что установленные Лобачевским уравнения, связывающие стороны и углы прямолинейного треугольника сами по себе алгебраически непротиворечивы и независимы – это никаких сомнений вызывать не может. Но допускают ли они ту геометрическую интерпретацию, которая с ними связана в неевклидовой геометрии, не приводят ли они к противоречию геометрическому, – в то время это оставалось далеко не ясным. Сам Лобачевский этим соображениям полной доказательной силы не присваивал. Именно поэтому он возвращается к этому вопросу, можно сказать, во всех своих работах и хочет пролить на него свет с разных сторон. Он ищет подтверждения своей вере в правильность созданной им геометрии, главным образом в ее приложениях к нахождению значений определенных интегралов. Замысел здесь заключается в следующем. Подынтегральное выражение, входящее под знак определённого интеграла, рассматривается как элемент длины, площади, объёма или массы в неевклидовой геометрии. Самый же интеграл, таким образом, выражает определённую длину, площадь, объём или массу. Это значение интеграла Лобачевскому часто удаётся разыскать средствами «воображаемой» геометрии. Значение определённого интеграла, таким образом, найдено при помощи неевклидовой геометрии. Когда это значение найдено, Лобачевскому обыкновенно удаётся его разыскать аналитически. В совпадении обоих результатов он видит подтверждение правильности «воображаемой» геометрии. Выражение длины окружности через радиус было найдено элементарными геометрическими средствами, но оно, конечно, может быть найдено также интегрированием дифференциала с учётом уравнения окружности. Точно также и площадь круга может быть вычислена тем и другим путём. Лобачевский нашёл выражение для площади треугольника интегрированием дифференциала; оно может быть получено чисто геометрическими средствами. Но это только простейшие совпадения; Лобачевский их чрезвычайно углубляет и расширяет. Лобачевскому действительно удалось этим путём разыскать значения многих определённых интегралов, главным образом таких, в которых фигурируют гиперболические функции. Справочники, содержащие значения определённых интегралов с указаниями авторов, разыскавших эти значения, пестрят именем Лобачевского. Иногда Лобачевскому не удаётся найти значение интеграла, но преобразованием переменных, которое диктуется переходом от одних координат в неевклидовом пространстве к другим, он очень удачно приводит одни определённые интегралы к другим, более простым. Либман называет гениальными эти многообразные интегральные вычисления. При всём том строгой доказательной силы в вопросе о непротиворечивости «воображаемой геометрии» эти результаты не имели. У тех, кто эти трудные вычисления производил, они, несомненно, порождают субъективную уверенность в том, что геометрия, которая к ним привела, не может быть противоречива. Но объективной уверенности в строгой логической правильности гиперболической геометрии они, конечно, не дают. Каждое такое вычисление может быть рассматриваемо как частичная проверка этого факта, но проверка общего утверждения на ряде частных случаев не даёт его доказательства. Такого доказательства и Лобачевский не даёт. Найти его было предоставлено следующим поколениям." 6. Вклад Н.И.Лобачевского в развитие науки Если геометрия Евклида является только часть геометрии Лобачевского, то выходит, что наш мир – не мир Евклида, как принято считать? Почему же мы не замечаем разницы? Как пример можно привести тот факт, что видимый звездный свод это ни что иное, как предельная плоскость. Астрономам после признания достижений Лобачевского пришлось пересчитывать все расстояния между звездами – и ошибки достигали 1/6. Как мы уже знаем, на поверхностях с отрицательной кривизной работает геометрия Лобачевского. Но именно эту кривизну имеют графики интенсивности всех электромагнитных полей. Состояние поверхности плазмы также описывается геометрией Лобачевского. Но наглядно геометрию Лобачевского можно устроить и на бумаге. Если нарисовать окружность, то мы можем, не выходя за ее пределы, провести сколько угодно прямых, не пересекающих данную. Взяв сферу, можно построить стереометрическую модель. Такая модель называется модель Клейна. Все эти модели служат одной цели – полнее представить наш мир, не прибегая к вселенским масштабом. Только в XIX веке Н.И.Лобачевский и другие математики пришли к мысли, что эти следствия образуют непротеворичивую геометрию, которую мы в настоящее время называем геометрией Лобачевского, и V поступает, не зависит от остальных аксиом геометрии Евклида. Критика теории отношений Евклида, которая у него была оторвана от теории числовых отношений, состояло в предложении объединить эти две теории в единую теорию, для чего, и следовало рассматривать геометрические величины как числа нового типа, мы в настоящее время эти числа называем действительными, или вещественными (Евклид знал только натуральные числа). Также подвергалось критике стремление Евклида избегать движение и наложение, к которому призывал Аристотель, эта установка Евклида критиковалась многими последующими геометрами, которые в своих трудах пользовались движением. Но все же, Евклид кое-где применял движение, следуя за своим предшественником. Создание и разработка геометрии Лобачевского поставили вопрос об исследовании всей структуры системы аксиом, как евклидовой геометрии, так и других возникающих к этому времени геометрий и выяснение независимости этих аксиом друг от друга. Заключение Наука прошла большой и сложный путь развития. Вместе с тем и человечество прошло длительный путь от незнания к знанию, непрерывно заменяя на этом пути неполное и несовершенное знание все более полным и совершенным. И пример тому - труды великих ученых-математиков: геометрия Евклида и геометрия Лобачевского. Возникшая из попыток доказательства пятого постулата неевклидова геометрия, открытая Н.И.Лобачевским, стала в наши дни необходимым аппаратом для изучения механики, физики, астрономии. Особенно важна геометрия Лобачевского для теории относительности. С другой стороны, открытие неевклидовой геометрии привело к новым исследованиям в области оснований геометрии и, в частности, к аксиоматике Гильберта. Открытие неевклидовой геометрии не только сыграло огромную роль в развитии новых идей и методов в математике, естествознании, но и имеет и философское значение. Господствующее до Лобачевского мнение о незыблемости геометрии Евклида в значительной мере основывалось на учении известного немецкого философа И.Канта (1724-1804), родоначальника немецкого классического идеализма. Открытие неевклидовой геометрии доказало, что нельзя абсолютировать представления о пространстве, что «употребительная» (как называл Лобачевский геометрию Евклида) геометрия не является единственно возможной. Итак, в основе геометрии Евклида лежат не априорные, врожденные уму понятия и аксиомы, а такие понятия, которые связаны с деятельностью человека, с человеческой практикой. Только практика может решить вопрос о том, какая геометрия вернее излагает свойства физического пространства. Открытие неевклидовой геометрии дало решающий толчок грандиозному развитию науки, способствовало и поныне способствует более глубокому пониманию окружающего нас материального мира. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ Книги:
WEB ресурсы: 1.https://geom.kgsu.ru/index.php-Н.И.Лобачевский-создатель неевклидовой геометрии Приложения  рисунок 2 рисунок 2 рисунок 3 рисунок 3 рисунок 4 рисунок 4 рисунок 5 рисунок 5 рисунок 6 рисунок 6 рисунок 7 рисунок 7 рисунок 8 рисунок 8 |