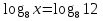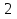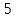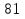«Логарифмы и их применение»
 Скачать 73.16 Kb. Скачать 73.16 Kb.
|
| государственное автономное учреждение среднего профессионального образования Калининградской области «Колледж сервиса и туризма» Методическая разработка открытого урока по учебной дисциплине «Математика» Тема: «Логарифмы и их применение» В группе по профессии: пекарь преподаватель: Пехова Н.Ю. Калининград 2012 Предмет: Математика Преподаватель: Пехова Надежда Юрьевна Тема урока: Логарифмы и их применение. Форма урока: урок-семинар. Педагогические технологии: компьютерные технологии обучения; Цели урока: - систематизация, закрепление и углубление знаний, умений и навыков обучающихся по применению свойств логарифмов; - развитие творческих способностей обучающихся, развитие навыков само- и взаимоконтроля; - воспитание культуры математической речи. Оборудование: доска, экран, медиапроектор, компьютерная презентация, рабочие тетради учебная литература, справочный материал. Основные этапы урока:
Ход урока:
а) Вычислите 10lg7. б) Вычислите log612+ log63. в) Вычислите log7196 – 2log72. г) Найдите х: 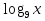 = 2 = 2д) Учебник (Алимов Ш.А.) №293(3)
Обучающиеся на листочках выполняют задания, обмениваются работами, сверяют ответы по заготовленному слайду, выставляют оценки согласно таблице.
Ответы:
11 – 12 правильных ответов - оценка «5» 9 -10 «4» 6 – 8 «3» 0 – 5 «2»
Учитель: слайд 6 Ребята, мы узнали о существовании логарифмов и их свойствах. Однако размеры школьного учебника не позволяют изложить всю историю возникновения и развития этого вопроса математики. Сегодня мы постараемся увидеть присутствие логарифмов в нашей жизни. В течение XVI в. Резко возрос объем работы, связанный с проведением приближенных вычислений в ходе решения разных задач, и в первую очередь задач астрономии, имеющей непосредственное практическое применение (в частности, при определении положения судов по звездам и по Солнцу). Наибольшие проблемы возникали, при выполнении операций умножения и деления. Открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию их логарифмов, облегчило жизнь вычислителей. Учащийся 1: слайд 7 Первый изобретатель логарифмов — шотландский барон Джон Непер (1550—1617) Учащийся 1: Потомок старинного воинственного шотландского рода. Изучал логику, теологию, право, физику, математику, этику. Увлекался алхимией и астрологией. Изобрел несколько полезных сельскохозяйственных орудий. В 1590-х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый труд "Описание удивительных таблиц логарифмов" опубликовал лишь в 1614 году. В конце 1620-х годов была изобретена логарифмическая линейка, счетный инструмент, использующий таблицы Непера для упрощения вычислений. С помощью логарифмической линейки операции над числами заменяются операциями над логарифмами этих чисел. Учитель: слайд 8 И ещё недавно трудно было представить инженера без логарифмической линейки в кармане. Затем логарифмическую линейку вытеснили калькуляторы. Но без логарифмической линейки не были бы построены ни первые калькуляторы, ни первые компьютеры . 2. Логарифмы в нашей жизни Учащийся 2: Слайд 10 Астрономы распределяют звезды по степеням видимой яркости на светила первой, второй, третьей и т.д. звездной величины. Физическая яркость звезд составляет геометрическую прогрессию со знаменателем 2,5. Поэтому «величина» звезды представляет собой не что иное,как логарифм ее физической яркости. Оценивая видимую яркость звезд, астроном оперирует с таблицей логарифмов, составленной по основанию 2,5 Учащийся 1: Слайд 11 Сходным образом оценивается и громкость шума. Вредное влияние промышленных шумов на здоровье рабочих и производительность труда побудило выработать приемы точной числовой оценки громкости шума. Единицей громкости служит «бел», практически – его десятая доля, «децибел». Громкость шума, выраженная в белах, равна десятичному логарифму его физической силы Слайд 12 Применение логарифмов Учащийся 2: Слайд 13 Музыка Так называемые ступени частот звуковых колебаний представляют собой логарифмы. Только основание этих логарифмов равно 2 (а не 10, как принято в других случаях). Номера клавишей рояля представляют собой логарифмы чисел колебаний соответствующих звуков. Учащийся 1: Слайд 14 Психология Изучая логарифмы, ученые пришли к выводу о том, что организм как бы «логарифмирует» полученные им раздражения. Здесь действует так называемый «психофизический закон Фехнера»: величина ощущения пропорциональна логарифму величины раздражения. Как видим, логарифмы вторгаюсь и в область психологии. 3. Логарифмическая спираль в природе и технике Слайды 15-16 Учитель: ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ, плоская кривая, описываемая точкой, движущейся по прямой, которая вращается около одной из своих точек О (полюса логарифмической спирали) так, что логарифм расстояния движущейся точки от полюса изменяется пропорционально углу поворота; логарифмическая спираль пересекает под постоянным углом a все прямые, выходящие из полюса. Логарифмическая спираль  Учащийся 2: Слайд 17 В математике логарифмическая спираль впервые упоминается в 1638 году Рене Декартом. Учащийся 1: Слайд 18 Один из наиболее распространенных пауков, сплетая паутину, закручивает нити вокруг центра по логарифмической спирали. Учащийся 2: Слайд 19 Хищные птицы кружат над добычей по логарифмической спирали. Дело в том, что они лучше видят, если смотрят не прямо на добычу, а чуть в сторону. Учащийся 1: Слайд 20 Живые существа обычно растут, сохраняя общее начертание своей формы. При этом чаще всего они растут во всех направлениях. Взрослое существо – и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться им приходится скручиваться, причем рост совершается так, что сохраняется подобие раковины с ее первоначальной формой. Учащийся 2: Слайд 21 Раковины моллюсков, улиток, рога млекопитающих, закручены по логарифмической спирали. Можно сказать, что эта спираль, является математическим символом соотношения формы и роста. Учащийся 1: Слайд 22 Семечки в подсолнухе расположены по дугам, близким к логарифмической спирали. Учащийся 2: Слайд 23 Шишка хвойного дерева. Распределение чешуек на конической поверхности отличается изяществом, рациональностью и совершенством геометрической формы. Весь конус развивается по двум спиралеобразным виткам. Учащийся 1: Слайд 24 По логарифмичесим спиралям закручены и многие Галактики, в частности Галактика, которой принадлежит Солнечная система. Учитель: Великий немецкий поэт Иоганн – Вольфганг Гете считал ее даже математическим символом жизни и духовного развития. IV. Работа группами (проверка усвоения материала) Слайд 25 1.Вычислите: 1) 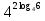 2)  3) 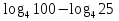 4)  2. Найдите х: 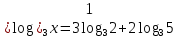 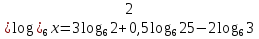 V. Подведение итога урока. Комментирование оценок. Задание на дом: № 298(1;2); № 305(1-3) Слайд 26 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
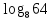
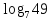
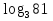

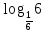


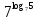

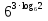
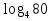 -
- 
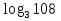 -
- 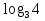
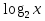 = 3
= 3 = 2
= 2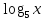 = 3
= 3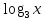 = 4
= 4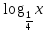 = -3
= -3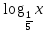 = -3
= -3