Конспект урока алгебры в 9 классе по теме «Функции, и свойства и графики»

Скачать 66.8 Kb. Название Конспект урока алгебры в 9 классе по теме «Функции, и свойства и графики» Дата 05.04.2016 Размер 66.8 Kb. Тип Конспект

Конспект урока алгебры в 9 классе по теме «Функции, и свойства и графики» Цели: 1) образовательная: повторить и систематизировать знания учащихся по теме линейная, квадратичная функции и обратная пропорциональность, актуализировать умения и навыки исследования основных видов функций. 2) воспитательная: воспитание внимательности, интереса к изучаемому предмету, сообразительности; 3) развивающая: развитие памяти, любознательности, активности, умения обобщать изучаемые факты. Оборудование: мультимедиа, раздаточный материал, опорный конспект, материал по повторению Ход урока Организационный момент. ( Сообщение темы и целей урока ) Устная работа. 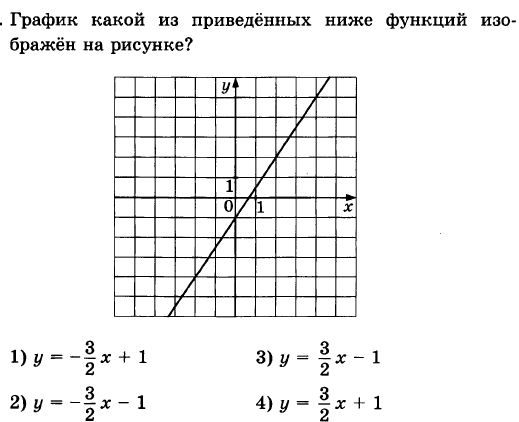1). 2) 3) 4). №1 №2 III. Проверка домашнего задания. Рассказать свойства функций IV. Повторение учебного материала. 2. А к т у а л и з и р о в а т ь з н а н и я об основных видах функций, изученных в курсе математики. 1) линейная 2) квадратичная 3) обратная пропорциональность 1) Линейная функция Формула у = kx + b Графиком является прямая линия. b – ордината пересечения с осью у Если b = 0 , то прямая проходит через начало координат. - это угол между прямой и положительным направлением оси Ох. Если k > 0, то угол - острый Если k < 0, то угол - тупой Обобщенный материал представить в виде опорного конспекта (таблицы): 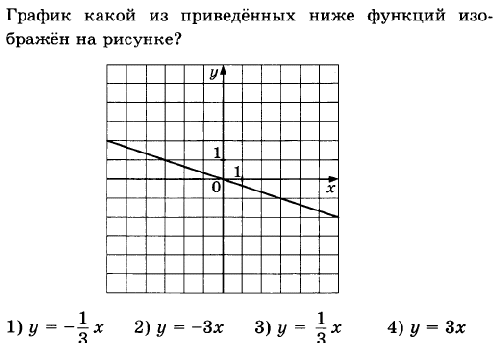Линейная у = kx + b D (f) = R k > 0, b ≠ 0 k < 0, b ≠ 0 k = 0 b = 0, k ≠ 0 Прямая пропор- циональность Графиком линейной функции является прямая. Для построения графика достаточно построить две точки и соединить прямой линией . 2) Квадратичная функция Формула у = аx2 + bx + с, а ≠ 0 Графиком является парабола. с – ордината пересечения с осью у Если а > 0, то ветви параболы направлены вверх Если а < 0, то ветви параболы направлены вниз. х0 = - абсцисса вершины параболы Квадратичная у = аx2 + bх + с, а ≠ 0 D (f) = R а > 0 а < 0 Графиком квадратичной функции является парабола, ветви которой направлены вверх при а > 0 и вниз при а < 0. Д л я п о с т р о е н и я п а р а б о л ы н у ж н о: 1) Найти координаты вершины параболы и отметить ее в координатной плоскости. 2) Построить еще несколько точек, принадлежащих параболе. 3) Соединить отмеченные точки плавной линией 3) Обратная пропорциональность Формула у = , х ≠ 0 Графиком является гипербола. Если k > 0, ветви гиперболы расположены в I и III координатных плоскостях Если k < 0, то во II и IV Обратная пропорциональность y = D (f) = R \ {0} k > 0 k < 0 Графиком функции y = является гипербола. Строим одну ветвь гиперболы по точкам, вторую получаем «отражением» относительно начала координат V. Формирование умений и навыков. Упражнения: № 1018, № 1019, № 1020 (устно). № 1021 (д, е). Р е ш е н и е д) у = 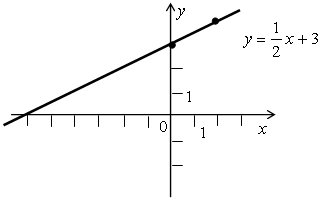x + 3 – линейная функция, график – прямая: х 0 2 у 3 4 е) у = 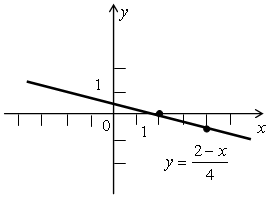; у = x + – линейная функция, график – прямая: х 2 4 у 0 № 1022, № 1024 (устно). При решении этих упражнений вспоминаем о «механическом» преобразовании графиков функций. № 1026. Р е ш е н и е у = –0,5х2 + х + 1,5 – квадратичная функция, график – парабола, ветви которой направлены вниз. Найдем координаты вершины параболы и точек ее пересечения с осью х и осью у. А (х0, у0); х0 = = 1; у0 = –0,5 · 12 + 1 + 1,5 = 2. А (1; 2) – вершина параболы. –0,5х2 + х + 1,5 = 0; 5х2 – 10х – 15 = 0; х1 = –1; х2 = 3; (–1; 0); (3; 0) – точки пересечения с осью х. Если х = 0, то у = 1,5. (0; 1,5) – точка пересечения с осью у. 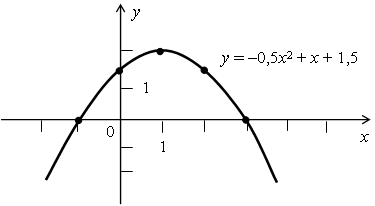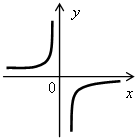О т в е т: у = 0, если х = –1 или х = 3; у > 0, если х (–1; 3); у < 0, если х (–∞; –1) (3; +∞). Функция возрастает на (–∞; 1]. Наибольшее значение функции равно 2. № 1030 (а). Р е ш е н и е у = – обратная пропорциональность, графиком является гипербола, расположенная в I и III координатных четвертях. D (у) = (–∞; 0) (0; +∞). Построим ветвь гиперболы для х > 0. х 1 2 4 8 16 у 16 10 8 4 2 1 О т в е т: у > 0, если х > 0; у < 0, если х < 0. VI. Самостоятельная работа. Группа С 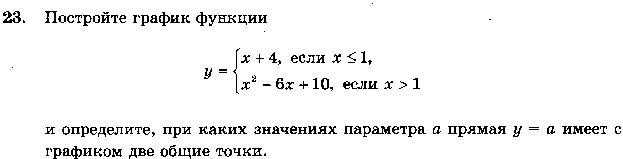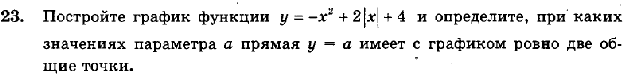VII. Итоги урока. В о п р о с ы у ч а щ и м с я: – Какая зависимость называется функцией? – Назовите основные свойства линейной функции, квадратичной, обратной пропорциональности. – Приведите алгебраическую и геометрическую интерпретацию указанных свойств. Домашнее задание: № 1021 (г), № 1025, № 1027, № 1028 (а, д).