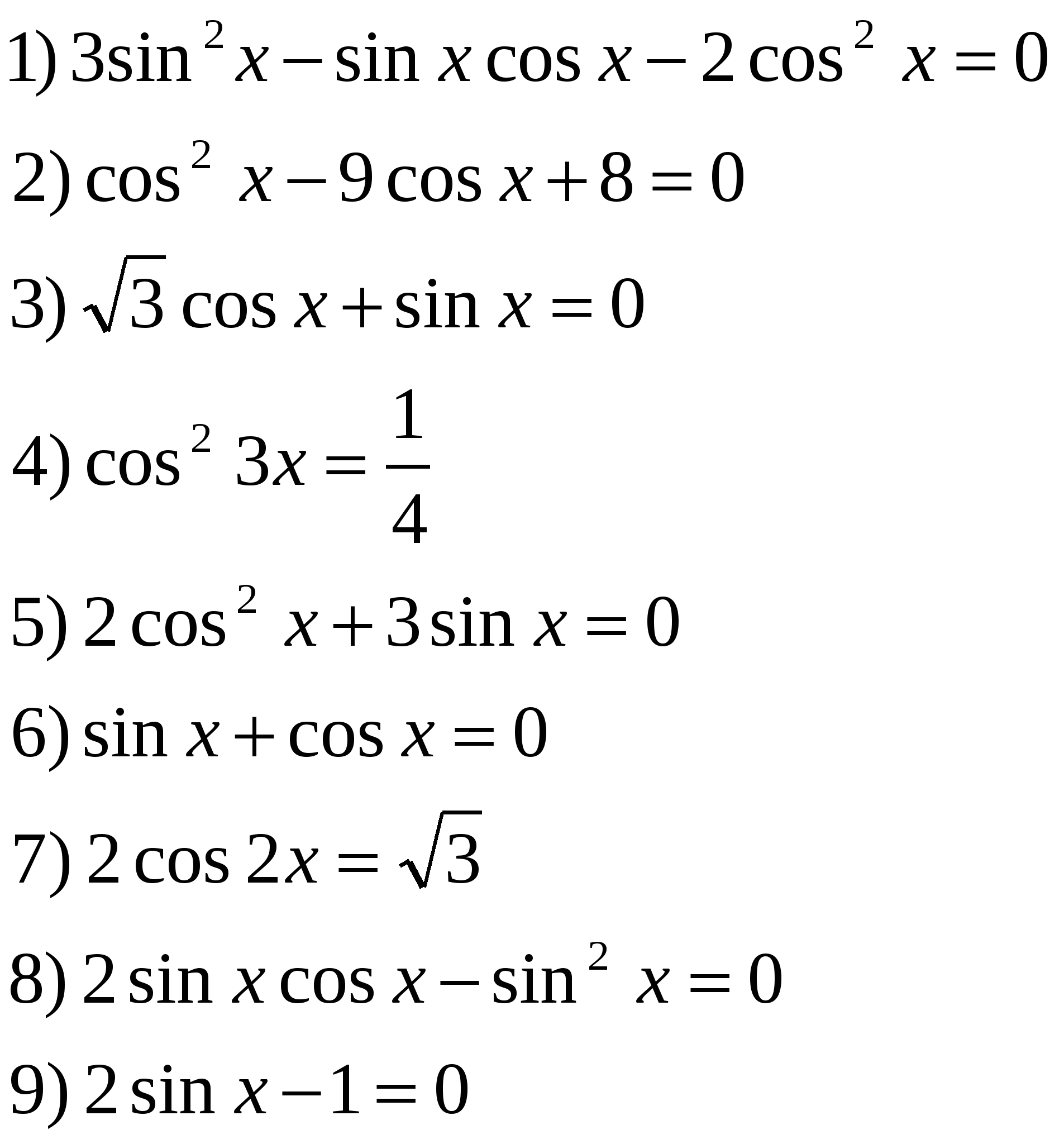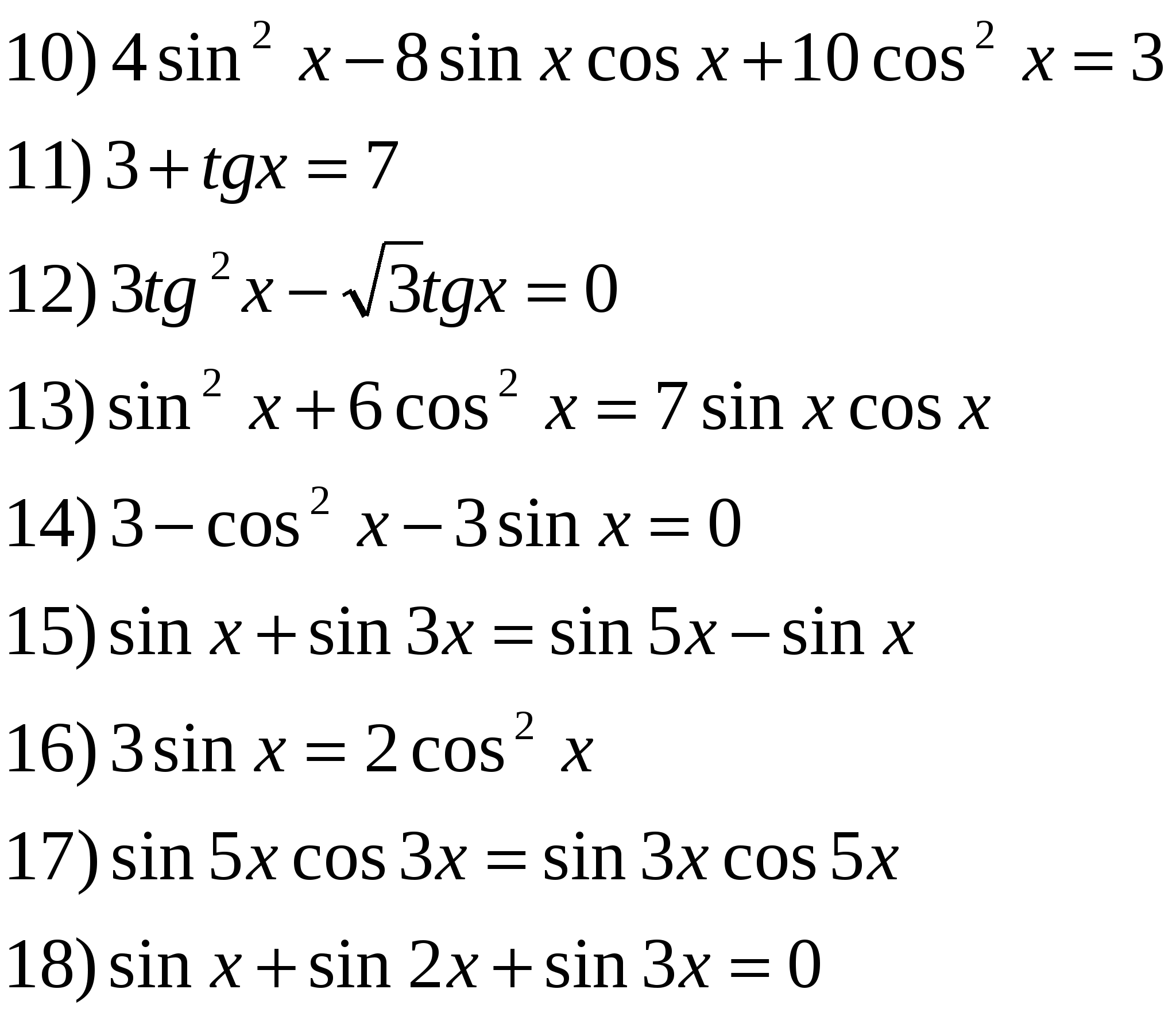Дидактический материал

Скачать 39.37 Kb. Название Дидактический материал Дата 05.03.2016 Размер 39.37 Kb. Тип Документы

Дидактический материал 1) Вычислите: а) arccos (–1); б) arcsin 0; в) arctg 0; г) arcctg 1; д) arcsin; е) arccos; ж) arcctg; з) arctg (–). 2) Поставьте вместо звездочек знак равенства или неравенства так, чтобы получилось истинное высказывание: а) arcsin 1 arccos 1; б) arcsin 1 arctg 1; в) arcsin (–1) arctg (–1); г) arcsin arccos; д) arccos arcsin 3. Проверочная работа. В таблицу впишите ответы на вопросы Вариант 1 1 2 3 4 5 6 7 8 9 10 11 12 4. Установить соответствие: «Уравнение ↔ Корни». 5. Классификация уравнений по способам решений Рассматриваем типы тригонометрических уравнений и из набора уравнений выбираем уравнения каждого типа. Ответы: 1. Простейшие тригонометрические уравнения. ________________________ 2. Решения уравнений с помощью замены переменной. __________________ 3. Решение уравнений разложением на множители. _____________________ 4. Решение однородных уравнений I степени. __________________________ 5. Решения однородных уравнений II степени. _________________________ 6. Решение уравнений с помощью основного тригонометрического тождества. ____________ 7. Решение уравнений с помощью формул суммы и разности аргументов. ________________ 8. Решение уравнений с помощью формул понижения степени _________________________ 9. Решение уравнений с помощью преобразования сумм тригонометрических функций в произведение. ______________________ 6. Диагностика Вариант 1. 1) Все корни уравнения cos x = a находятся по формуле: А) + 2 Б) х = В) + Г) х = 2) Решите уравнение cos x = А) Б) х = В) х = Г) х = 3) Найдите корни уравнения: cos x = 1. А) х = Б) х = В) х = Г) х = Решите уравнения: А) Б) Дидактический материал 1) Вычислите: а) arccos (–1); б) arcsin 0; в) arctg 0; г) arcctg 1; д) arcsin; е) arccos; ж) arcctg; з) arctg (–). 2) Поставьте вместо звездочек знак равенства или неравенства так, чтобы получилось истинное высказывание: а) arcsin 1 arccos 1; б) arcsin 1 arctg 1; в) arcsin (–1) arctg (–1); г) arcsin arccos; д) arccos arcsin 3. Проверочная работа. В таблицу впишите ответы на вопросы Вариант 2 1 2 3 4 5 6 7 8 9 10 11 12 4. Установить соответствие: «Уравнение ↔ Корни». 5. Классификация уравнений по способам решений Рассматриваем типы тригонометрических уравнений и из набора уравнений выбираем уравнения каждого типа. Ответы: 1. Простейшие тригонометрические уравнения. ________________________ 2. Решения уравнений с помощью замены переменной. __________________ 3. Решение уравнений разложением на множители. _____________________ 4. Решение однородных уравнений I степени. __________________________ 5. Решения однородных уравнений II степени. _________________________ 6. Решение уравнений с помощью основного тригонометрического тождества. ____________ 7. Решение уравнений с помощью формул суммы и разности аргументов. ________________ 8. Решение уравнений с помощью формул понижения степени _________________________ 9. Решение уравнений с помощью преобразования сумм тригонометрических функций в произведение. ______________________ 6. Диагностика Вариант 2. 1) Все корни уравнения sin x = a находятся по формуле: А) х = Б) х = В) Г) 2) Решите уравнение: sin x = . А) Б) В) Г) х = 3) Найдите корни уравнения: sin x = 1. А) х = Б) х = В) х = - Г) х = 2 Решите уравнения: А) Б)