|
Конспект урока алгебра и начала анализа в 11классе Тема урока: «Использование свойств функций в решении нестандартных уравнений» Цели: Образовательные
Конспект урока алгебра и начала анализа в 11классе
Тема урока: «Использование свойств функций в решении нестандартных
уравнений»
Цели:
Образовательные:
1.Обобщить, дополнить и систематизировать вопросы, связанные со свойствами функций.
2. Вооружить учащихся специальными умениями и методами решения нестандартных уравнений.
3. Научить применять эти методы, уметь их квалифицировать.
Развивающие:
4. Развивать логическое мышление и интуицию при решении
нестандартных уравнений.
Воспитательные:
5. Формировать отношение к образованию, как важному и
необходимому.
Воспитывать потребность в навыках самоконтроля.
Оформление.
1 доска Стенд с заданиями ЕГЭ.
Цели урока, сформулированные для учащихся.
1. Обобщить, дополнить и систематизировать вопросы, связанные со свойствами функций.
2. Познакомиться с нестандартными методами решения уравнений.
3. Научиться применять эти методы, уметь их квалифицировать.
Домашнее задание: Никольский 11кл. стр.305
№12.6(в),12.13(а),12.23(а).
2 доска Эпиграф «Задача - это как будто крепость, ее решение - это
награда победителю»
На 2 и 3 досках записаны условия уравнений 4 типа, закрытые листами.
В процессе решения лист с условия уравнения снимается.
1) log3(1-2x)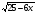 =14 =14
2) 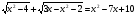
3) cos 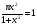
4) sin3x-3 sinx=4
5) lg2(x2-3x-9)+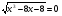
6) 2-x-2=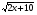
7) 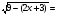 sin 2 sin 2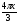 +3 +3
Мультимедийный проектор, экран, 2 презентации -27 слайдов.
Класс разбит на 5 групп по 4 ученика. В кабинете столы стоят для каждой группы, на столах таблички с фамилиями учеников.
4 ученика работают за компьютерами, решая 1 часть (В) задания ЕГЭ.
Деятельность учителя
|
Деятельность ученика
|
длительность
|
Подготовительный этап.
|
|
7мин.
|
Добрый день всем!
Поприветствуем наших гостей.
Садитесь. 12.02.2010.
Тема урока. «Использование свойств функций в решении нестандартных уравнений»
Тема функции и их свойства полно и многообразно пред-ставлены на ЕГЭ. Следует от-метить, что на данном этапе подготовки к обязательному экзамену удобнее классифици-ровать уравнения не по внеш-нему виду: логарифмическое, показательное, тригонометри-ческое и т.д, а по способам ре-шения. Так как большинство
уравнений на экзамене трудно отнести к какому-то одному виду. Чаще всего они смешан-ные. Там есть и логарифмы, и
тригонометрия, и иррацио-нальность и т.д. И часто их не возможно решить алгебраичес-кими способами.
Цель урока.
Вспомним основные свойства функций.
Что называется областью определения функции?
Дайте определение об-ласти значения функции.
Какие функции называ-ются неотрицательными?
Какие функции называ-ются возрастающими на промежутке?
Какие функции называ-ются убывающими на промежутке?
Дайте определение огра-ниченных функций.
|
На экране 1 слайд
На экране 2 слайд
На экране 3-9 слайды
каждый слайд с анимацией, как только ученики ответили на вопрос по щелчку дублируется определение.
На экране 6 слайд
На экране 7 слайд
На экране 8 слайд
На экране 9 слайд
|
|
Основной этап.
|
|
15мин.
|
Актуализация знаний
|
|
|
5групп – выбирают карточки с заданием. Карточки составле-ны по методам решения. Каж-
дая группа анализирует (поста-райтесь, может быть интуити-вно) и определяет свойство функции, которое определит метод решения уравнения.
Переходим к решению нестан-дартных уравнений 2части (С) ЕГЭ
Пока ученики определяют свойства функции и метод ре-шения я подхожу к каждой группе, направляя их, оказывая помощь, чтобы придать им уверенность в своих возможностях.
К доске выходит желающий с 1 карточкой.
Вопрос: 1.Каковы особенности функций, входящих в уравне-ние?
2.Что важно для каж-дой из этих функций?
Проверим, есть еще корни?
Определите монотонность функций левой и правой.
Каким свойством объединены уравнения 2 карточки?
К доске выходит- желающий.
Найдем те значения к, при которых равенство верно.
Вопрос: 1. Обратите внимание на дробь, что можно утверж-дать о значении дроби?
Сравните знамена-тель и числитель.
перейдем от дроби к 2к.
К доске выходит еще один ученик 2 группы.
Обратим внимание на функции левой части.
Вопрос: 1.Что важно для функ- ции sint?
2. В данном уравнении важна какая часть неравенства?
3. Какую систему составляем?
Здоровье сберегающие технологии.( «море»)
Рассмотрим следующую груп-пу уравнений в карточке 3.
К доске выходит член группы.
Обратим внимание на каждое слагаемое левой части.
Метод: неотрицательность функций.
Рассмотрим уравнения 4группы. Какое свойство функций связывают эту группу
Вопрос: Какова монотонность каждой из функций?
Что известно о точке пересече-ния графиков функций?
В левой части степень 2, а в правой части полный квадрат.
Осталась последняя группа уравнений.
Обратите внимание на
sin 2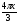 . .
Мы оценили правую часть, имеем уравнение, следователь-но и левая часть в этих грани-цах.
Имеем квадрат суммы меньше или равен 0. Какой вывод надо сделать?
Мы с К. Д. разобрали
Задачу С-6 с параметром.
Решение сопровождается показом слайдов.
Контроль.
Смотрим на экран. Определите метод решения предложенных уравнений.
По каждому уравнению идет
обсуждение.
Представьте себе, что наш урок – это море. Кто-то бросается в пучину, кто-то спокойно плавает или лежит на морском берегу. Как вы себя ощущаете в этом прост-ранстве? Вам приятно, все понятно, а кто-то устал, а может спрятаться за тот утес?
Включаю музыку. Слайд -море
Объявляю оценки за работу.
Всем спасибо за работу!
|
Ребята, работающие за компью-терами, присоединяются к своим группам. На каждом компьютере
в программе ЕГЭ есть дневник, где выставляется оценка. Таким образом 4ученика знают свою оценку.
На экране 10 слайд
1.Использование области определения
2. Использование множества значений
3. Неотрицательности функций
4. Монотонность функций
5. Метод оценки
слайд с анимацией, как только ученики ответили на вопрос, по щелчку дублируется метод решения
log3(1-2x)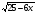 =14 =14
Ответ. 1.Уравнение содержит log3(1-2x) и корень четной степени.
2.Логарифм существует только для положительных чисел, корень четной степени существует для неотрицательных чисел.
Решение
1-2x>0, x<0,5
25-6х≥0? x≤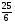 , x<0,5 , x<0,5
log3(1-2x)= найдем подбором корень. Х= - 4 найдем подбором корень. Х= - 4
Ответ: 1. у= log3(1-2x) убывающая,
у= возрастающая. возрастающая.
2. Графики функций имеют не более одной общей точки.
Корень х = - 4
Метод область определения
Использование множества значений
cos 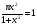
Решение:
 2к 2к ,кєz ,кєz
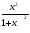 =2к, кєz =2к, кєz
0≤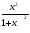 <1 <1
0≤ 2к<1
к=0, значит х=0 Корень равен 0
sin3x-3sinx=4
Ответ: 1.Эта функция ограничена.
Решение:
-1 ≤ sin3x≤1
-3≤ -3sinx ≤3
-4 ≤ sin3x-3sinx≤4
2. Правая, где равенство 4.
sin3x=1, 3х= , ,
-3sinx=3; х=- ;кєZ ;кєZ
Ответ:  х= - х= - ;кєZ ;кєZ
Метод неотрицательность функций.
g2(x2-3x-9)+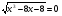
Ответ: слагаемые левой части неотрицательны, а в правой части 0! Значит имеем систему, где каждое слагаемое левой части равно 0
. lg(x2-3x-9)=0, x2-3x-9=1,
х3-8х-8=0; x2-3x-10=0,
х=5,
х= -2.
Проверка:
х=5, 125-40-8=0 не верно,
х= -2, -8+16-8=0 верно, -2корень
Ответ: -2.
Ответ: Свойство монотонности
Метод монотонности
2-x-2=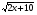
у=2-x-2 убывающая функция
у=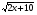 возрастающая функция возрастающая функция
Если графики функций пересека-
ются то имеют не более одной общей точки.
Найдем корень уравнения подбором, т.к. х ≥ -5
Х= -3.
Ответ: -3.
Метод оценки.
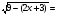 sin 2 sin 2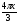 +3 +3
эта функция ограничена, т.е.
0≤sin 2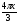 ≤1 ≤1
3≤ sin 2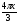 +3≤4 +3≤4
3 ≤ ≤4 ≤4
9 ≤ 9-(2х+3)2 ≤16
0 ≤ -(2х+3)2≤7
-7 ≤ (2х+3)2≤0
(2х+3)=0
х = -1,5
Ответ: -1,5.
Сообщение одиннадцатиклас-сника.
Я с помощью слайдов покажу еще нестандартный метод решение уравнения с помощью производной.
Задача
Найти все значения Р, при кото-рых уравнение 4C0S 3х+p=3C0S2x
не имеет решения.
Решение:
Выполним тождественное преобразование:
4сos 3х + р =3сos2х
3сos 2х-4сos 3х=р
Приведем к одному аргументу и одной функции.
Р=3(2C0S 2Х-1) -4C0S 3Х
Р=6C0S 2Х – 3 -4C0S 3Х ,
cosX=t, |t|≤1
Рассмотрим f(t)=6t2 -3- 4t3
6t2 -3- 4t3-многочлен,
f(t) непрерывная и дифференцированная функция
F(t)= 6t2 -3- 4t3
F`(t)=12t- 12t2
Найдем критические точки.
F`(t)=0; следов. 12t-12t2=0
12t(1-t)=0
t=0 или t=1,т.к. |t|≤1,
0 и 1 критические точки
f(-1)=7 наибольшие
f(0)=-3 наименьшие
f(1)=-1
Е(f)= [-3;7],таким образом
все значения Р, при которых уравнение не имеет решения
Рє(-∞ 3)  (7; ∞) (7; ∞)
Ответ: Рє(-∞ ) (7; ∞) (7; ∞)
Презентация. Слайды 1-6
Слайды с анимацией по ходу обсуждения по щелчку включаю необходимую информацию.
log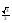 (x+3)= (x+3)=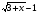
монотонность и подбор
12+12x+4x2=(sin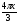 +√3)( √3- sin +√3)( √3- sin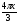 ) )
оценки
(log2(x-5)- sinπx)2+(x-6)2=0
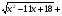 |sin(lg(x-1))|=0 |sin(lg(x-1))|=0
неотрицательность функций.
Слайд -море, звучит музыка.
Учащиеся говорят о своем состоянии.
Слайд «Всем спасибо!»
|
2мин.
5мин.
5мин.
3мин
| |
|
|
 Скачать 100.3 Kb.
Скачать 100.3 Kb.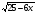 =14
=14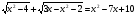
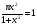
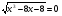
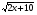
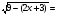 sin 2
sin 2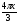 +3
+3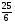 , x<0,5
, x<0,5 найдем подбором корень. Х= - 4
найдем подбором корень. Х= - 4 2к
2к ,кєz
,кєz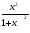 =2к, кєz
=2к, кєz ,
, х= -
х= - ≤4
≤4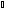 (7; ∞)
(7; ∞)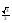 (x+3)=
(x+3)=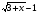
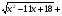 |sin(lg(x-1))|=0
|sin(lg(x-1))|=0