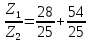Комплексные числа. Действия над комплексными числами в алгебраической форме
 Скачать 132.46 Kb. Скачать 132.46 Kb.
|
| Комплексные числа. Действия над комплексными числами в алгебраической форме. I.Организационный момент II. Введение Мы никогда не стали бы разумными, если бы исключили число из человеческой природы. Платон III. Актуализация знаний. Решите квадратное уравнение.
Мы видим, что одно уравнение имеет два корня, один корень или два одинаковых корня, и не имеет решений в множестве действительных чисел. Сегодня мы с вами узнаем, что и это уравнение решить можно, только для этого нам придется познакомиться еще с одним множеством чисел. Давайте вспомним, а какие множества чисел мы с вами знаем? (Вспоминаем беседуя)
Множество натуральных чисел обозначается латинской буквой N ={1,2,3,....}
3)Множество целых чисел состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0. Целые числа обозначаются латинской буквой Z={…-3,-2,-1,0,1,2,3,....}. 4) Вы взяли и разрезали яблочко на три равные части. Каждая часть составляет  Рациональные числа – это числа, представимые в виде дроби 5) Потом оказалось, что вычисляя длину диагонали квадрата или гипотенузу прямоугольного треугольника, мы получили число под знаком корня.  , такие числа мы стали называть иррациональными. , такие числа мы стали называть иррациональными.Все перечисленные множества чисел вместе мы стали называть множеством действительных чисел. Вывод: Для перечисленных выше множеств чисел справедливо следующее высказывание: 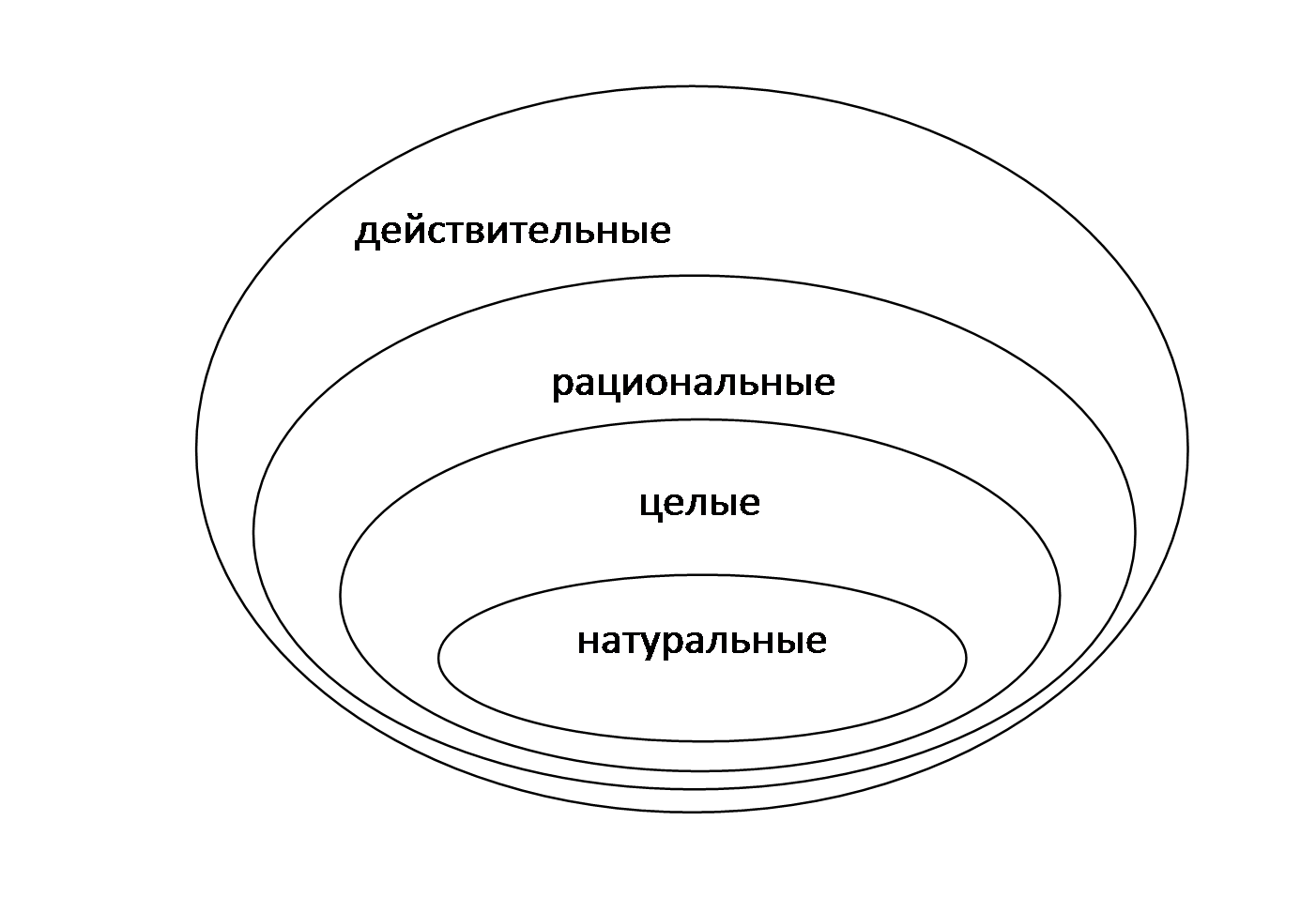 6) Что вы слышали о комплексных числах? Рассмотрим квадратное уравнение x2 = – 1. Оно на множестве действительных чисел решений не имеет, так как среди действительных чисел нет такого числа, квадрат которого отрицателен. Таким образом, действительных чисел явно недостаточно, чтобы построить такую теорию квадратных уравнений, в рамках которой каждое квадратное уравнение было бы разрешимо. Это приводит к необходимости расширять множество действительных чисел до множества, в котором было бы разрешимо любое квадратное уравнение. Такое множество называется множеством комплексных чисел и обозначается С. Мы пришли к введению понятия мнимой единицы i= Давайте подробнее поговорим о ней и попробуем вычислить: i2 , i4, i3, i5. i2=-1, тогда i4=-1∙(-1)=1 i3=( В ходе урока вы подробнее познакомитесь с действиями над мнимой единицей. Опр. Комплексным числом Название “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт. В 1777 году один из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа Этот символ вошел во всеобщее употребление благодаря К. Гауссу. Термин “комплексные числа” так же был введен Гауссом в 1831 году. Задание: Назовите мнимую и действительную часть комплексного числа.
Какой можно сделать вывод? Любое действительное число можно назвать комплексным с мнимой частью равной 0! 1. Действительное число а может быть также записано в форме комплексного числа: a+ 0 i или a – 0 i. Например, записи 7 + 0 i и 7 – 0 i означают одно и то же число 7 . 2. Комплексное число 0+ bi называется чисто мнимым числом. Запись bi означает то же самое, что и 0+ bi. 3. Два комплексных числа a+ bi и c+ di считаются равными, если a= c и b= d. Так же как и с действительными числами с мнимымы можно выполнять арифметические операции. Сложение комплексных чисел  ; ; 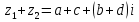 Пример 1 Сложить два комплексных числа Z1 = 5 + 8i Z2 = 4  3i 3iДля того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части: Z=9+5i Пример 2 Самостоятельно: Z1 =  4 + 10i Z2 = 6 + 7i Ответ: Z = 2 + 17i 4 + 10i Z2 = 6 + 7i Ответ: Z = 2 + 17iВычитание комплексных чисел  ; ; 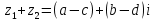 Пример 3 Найти разности комплексных чисел и, если, Z1 = 10 - 25i Z2 = 1-3i Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака: Z = (10  25i) 25i)  (1 (1 3i) = (10 3i) = (10  25i + 3i = 9 25i + 3i = 9  22i 22iПример 4 Самостоятельно: Z1 =  5+10i Z2 = 1+ 3i Ответ: Z = 5+10i Z2 = 1+ 3i Ответ: Z =  6+7i 6+7iУмножение комплексных чисел Правило умножения. Комплексные числа перемножаются как двучлены, при этом учитывается, что Пример 5 Найти произведение комплексных чисел Z1 = 1  i; Z2 = 3 + 6i i; Z2 = 3 + 6i 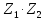 = (1 = (1  Z1∙Z2= Z2∙Z1 – от перестановки множителей произведение не меняется. Пример 6 Самостоятельно: Z1 = 5  2i Z2 = 1 2i Z2 = 1  4i Ответ: Z = 4i Ответ: Z =  3 3  22i 22iПример 7 Самостоятельно: ( 2+ 8i )( 2 – 8i )= 2 2 + 82 Вывод: ( a+ bi )( a – bi )= a 2 + b 2. Следовательно, произведение двух сопряжённых комплексных чисел равно действительному положительному числу. Деление комплексных чисел Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение. Пример 8. Найти 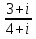 = = 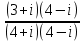 = = 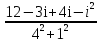 = =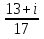 (Умножаем числитель и знаменатель на (4 -i)) Пример 9 Найти 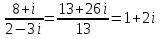 Пример 10 Вычислить: 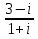 - (2+7i)(1 - i)= - 8 - 7i - (2+7i)(1 - i)= - 8 - 7iПример 11 Вычислить: 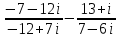 = -1 = -1Работа в парах Вариант 1. 1. Даны два комплексных числа Z1= (10 + 2i ) и Z2=(1 – 6i ). Найдите их сумму, разность, произведение и частное. 2. Проверьте правильность следующих утверждений: а) Сумма и разность чисто мнимых чисел есть чисто мнимое число. Для проверки возьмите числа: Z1=2i, Z2=-3i б) Произведение двух чисто мнимых чисел равно действительному числу. Для проверки возьмите числа: Z1=-5i, Z2=3i в) Квадрат чисто мнимого числа равен действительному отрицательному числу. Для проверки возьмите числа: Z1=10i г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу. Для проверки возьмите числа: Z1=7i, Z2=3 которых равны 2. Фамилия, имя:_______________ Оценка:_______ Фамилия, имя:_______________ Оценка:_______ Работа в парах Вариант 2. Даны два комплексных числа z1= (12 + 2i ) и z2=(3 – 4i ). Найдите их сумму, разность, произведение и частное. 2. Проверьте правильность следующих утверждений: а) Сумма и разность чисто мнимых чисел есть чисто мнимое число. Для проверки возьмите числа: Z1=2i, Z2=-3i б) Произведение двух чисто мнимых чисел равно действительному числу. Для проверки возьмите числа: Z1=-5i, Z2=3i в) Квадрат чисто мнимого числа равен действительному отрицательному числу. Для проверки возьмите числа: Z1=10i г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу. Для проверки возьмите числа: Z1=7i, Z2=3 Фамилия, имя:_______________ Оценка:_______ Фамилия, имя:_______________ Оценка:_______ Ответы:
а) Сумма и разность чисто мнимых чисел есть чисто мнимое число. Z1=2i, Z2=-3i , Z1+Z2=-i, Z1-Z2=5i б) Произведение двух чисто мнимых чисел равно действительному числу. Z1=-5i, Z2=3i , Z1 ∙Z2=15 в) Квадрат чисто мнимого числа равен действительному отрицательному числу. Z=10i , Z2=-100 г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу. Z1=7i, Z2=3, Z1 ∙Z2=21i Давайте, вспомним, с чего мы начинали урок? Как вы думаете, теперь мы с вами можем решить любое квадратное уравнение? Решение квадратных уравнений в поле комплексных чисел ax2 + bx + c = 0 1 cлучай: D>0, 2 корня, х1,2 = 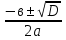 2 случай D=0, 1 коре нь, х =  3 cлучай: D<0, 2 корня, х1,2 = 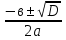 1. Решите уравнение x2 – 4x + 5 = 0. Решение. D = – 4 < 0, 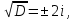 уравнение имеет мнимые корни: 2+i, 2-i уравнение имеет мнимые корни: 2+i, 2-i2. Решите уравнение x2 – x + 10 = 0. Решение. D = – 39 < 0, 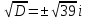 , уравнение имеет мнимые корни: , уравнение имеет мнимые корни:  3. Решите уравнение x2 – 4x + 13 = 0. Решение. D = – 36 < 0,  уравнение имеет мнимые корни: 2+3i, 2-3i уравнение имеет мнимые корни: 2+3i, 2-3i1. Решите уравнение x2 – 2x + 15 = 0. Решение. D = – 56 < 0, 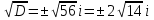 , уравнение имеет мнимые корни: , уравнение имеет мнимые корни: 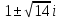 Домашнее задание: На «3»: 1. Даны два комплексных числа z1= (4 + 2i ) и z2=(1 – 3i ). Найти их сумму, разность, произведение и частное. На «4»: 1.Даны два комплексных числа z1= (5 + 2i ) и z2=(2 – 5i ). Найти их сумму, разность, произведение и частное. 2.Вычислить:  Ответ:a) 2 + i Ответ:a) 2 + iНа «5»: Решить уравнения: 1. х2 + (5 – 2i) x + 5(1– i) = 0; 2. х2 + (1 – 2i) х – 2i = 0; Рефлексия
|
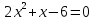 (ответ:
(ответ: 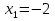 ;
;  )
) (ответ:
(ответ:  )
) (ответ: решений нет, т.к. D
(ответ: решений нет, т.к. D 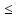 0)
0)