Использование технологии проблемного обучения на уроках математики как средство повышения познавательной активности учащихся
 Скачать 231.25 Kb. Скачать 231.25 Kb.
|
| Управление образования и науки администрации муниципального района «Алексеевский район и город Алексеевка» Использование технологии проблемного обучения на уроках математики как средство повышения познавательной активности учащихся Автор опыта: Острякова Елена Геннадьевна учитель математики и физики МОУ Репенская СОШ Алексеевского района Белгородской области г. Алексеевка 2012 Содержание: 1. Информация об опыте………………………………........ 3 2. Технология опыта……………………………………...... 8 3. Результативность опыта………………………………… 15 4. Библиографический список…………………………… 16 5. Приложения к опыту……………………………………..17 Раздел I. Информация об опыте
Свою педагогическую деятельность автор работы осуществляет в муниципальном общеобразовательном учреждении Репенская общеобразовательная школа Алексеевского района Белгородской области. Согласно социально-психологическому паспорту школы, большинство учащихся живут в семьях, в которых родители имеют среднее и среднее специальное образование. Каждый год классы пополняются учениками, прибывшими из разных регионов нашей страны, поэтому состав учащихся неоднороден по своей подготовленности и развитию. Педагогический коллектив школы работает над проблемой реализации современных образовательных технологий в процессе обучения школьников, что предполагает постоянный поиск неординарных форм организации учебно-воспитательного процесса. Изучив потребности и возможности обучающихся, автора опыта заинтересовала проблема развития познавательного интереса и творческих способностей учащихся на уроках математики. Началом работы по теме опыта стало проведение диагностики по определению внешней и внутренней мотивации учебной деятельности учащихся пятого и восьмого классов:
Результаты диагностики показали, что при переходе из ступени начального обучения к основному общему снижается внутренняя мотивация учебной деятельности. Для изучение уровня познавательной активности, использовался метод диагностики мотивации учения и эмоционального отношения к учению, основанный на опроснике Ч.Д. Спилбергера (модификация А.Д.Андреевой,1987год). При анализе результатов оказалось, что у учащихся этих групп только 4% с высоким уровнем познавательной активности, 50% находятся на среднем уровне, 46% - низком уровне. Необходимость создания условий для повышения мотивации обучения, а, следовательно, и познавательной активности при изучении математики привела к мысли автора работы о применении в своей педагогической деятельности технологии проблемного обучения. 1.2. Актуальность опыта. Модернизация образования ставит перед общеобразовательной школой новые задачи: формирование целостной системы универсальных знаний, умений, навыков, а также опыт самостоятельной деятельности и личной ответственности, т.е. ключевые компетентности, определяющие современное качество содержания образования. Проблема развития познавательной активности учащихся в условиях современной школы имеет очень большое значение. Содержание учебного материала, традиционные методы обучения и формы организации учебного процесса не способствуют в полной мере динамичному развитию познавательной активности школьников. Таким образом, обнаруживается противоречие между необходимостью повышения уровня познавательной активности учащихся и недостаточной технологической проработкой этого процесса в условиях традиционного обучения.
Ведущей педагогическая идея опыта заключается в  создании необходимых условий, содействующих повышению познавательной активности учащихся на уроках математики на основе использования технологии проблемного обучения. создании необходимых условий, содействующих повышению познавательной активности учащихся на уроках математики на основе использования технологии проблемного обучения.
Работа над опытом осуществлялась в течение четырёх лет с апреля 2008г. по май 2012 года и была разделена на следующие этапы: 1 этап – теоретический (апрель-май 2008 года), который предполагал обнаружение проблемы, теоретическое ее изучение и выявление уровня познавательных интересов учащихся. 2 этап – практический (сентябрь 2008 по январь 2012 года), в рамках которого использовались элементы технологии проблемного обучения, и отслеживалась эффективность применения отдельных форм, методов и средств обучения. 3 этап - заключительный (февраль-май 2012года), где проводилась диагностика и оценивалась результативность использования выбранных форм, методов и средств обучения.
Диапазон опыта включает работу автора по повышению познавательной активности в рамках урока математики В урочной системе технологию проблемного обучения автор использует на уроках изучения нового материала, уроках-практикумах, уроках-обобщениях, на уроках повторения изученного, при подготовке к выпускным экзаменам, в процессе индивидуальной работы с учащимися. Создание проблемных ситуаций позволяет выявлять и совершенствовать способности учащихся, развивать познавательную активность, мыслительные навыки.
Проблемное обучение это не абсолютно новое педагогическое явление. Элементы проблемного обучения можно увидеть в эвристических беседах Сократа, в разработках уроков для Эмилля у Ж.Ж.Руссо (1712-1778гг.). Ж.Ж.Руссо высказывал интересные мысли по активизации познавательной и творческой активности. Он говорил, что «ребёнок должен не выучить науку, а, выдумывая её, сам открывать знания для себя»[1]. Одним из важнейших путей активизации творчества Руссо считал постановку проблем перед учащимися, которые бы «озабочивали» его в течение долгого времени и побуждали к самостоятельному поиску решения, исследованию предмета или явления. Понятие «проблемное обучение» получило в 20-30 годы прошлого века. Проблемное обучение основывается на теоретических положениях американского философа и педагога Джона Дьюи (1859-1952). Согласно философским и психологическим воззрениям автора, мыслить человек начинает тогда, когда сталкивается с трудностями, преодоление которых имеет для него большое значение. Впоследствии за трудностями, которые надо преодолевать, закрепилось понятие проблема. Условием успешного обучения по Дж. Дьюи является: - проблематизация учебного материала (знание, удивление и любопытство); - активность ребёнка (знания должны усваиваться с аппетитом); - связь обучения с жизнью ребёнка, игрой, трудом. Позднее в 60-70 годы, учитывая всё положительное, что было накоплено в теории проблемного обучения, этим направлением в методике обучения занимались такие педагоги и психологи: Дж. Брунер – США, В. Оконь – Польша, в нашей стране М.Н. Скаткин, И.Я. Лернер, М.И. Махмутов, А.М. Матюшкин, Т..В. Кудрявцев и др. Т.В. Кудрявцев даёт проблемному обучению следующее толкование: «Проблемное обучение заключается в создании перед учащимися проблемных ситуаций, осознания и разрешения ими этих ситуаций при максимальной самостоятельности и под общим направляющим руководством преподавателя».[6] Толкование проблемного обучения по М.И. Махмутову заключается в следующем: «… проблемное обучение есть целенаправленная деятельность учителя и учащихся по постановке учебных проблем, их формулировке, выдвижению гипотез, их обоснованию и проверке на практике. Вся эта умственная работа учащимися проходит под руководством учителя и направлена на усвоение новых знаний, выработку умений и навыков, развитие умственных способностей и формированию интеллектуально активной личности».[8] При проблемном обучении не исключается объяснение учителя и выполнение учащимися задач и заданий, требующих репродуктивной деятельности, но принцип поисковой деятельности преобладает. В результате поисковой деятельности формируется опыт творческого усвоения знаний. И, что ещё важнее, происходит усвоение способов творческой деятельности. Активность ученика заключается в том, что он, сравнивая, анализируя, систематизируя, обобщая, конкретизируя фактический материал, сам получает новые знания. Суть активизации учения школьника посредством проблемного обучения состоит в активизации его мышления путём создания проблемных ситуаций, в формировании познавательного интереса и моделирования умственных процессов. А. М. Матюшкин характеризует проблемную ситуацию как «особый вид умственного взаимодействия объекта и субъекта, характеризующийся таким психическим состоянием субъекта (учащегося) при решении им задач, который требует обнаружения (открытия или усвоения) новых, ранее субъекту неизвестных знаний или способов деятельности». Иначе говоря, проблемная ситуация – это такая ситуация, при которой субъект хочет решить какие-то трудные для себя задачи, но ему не хватает данных и он должен сам их искать.[12] Как показали исследования, можно выделить наиболее характерные для педагогической практики типы проблемных ситуаций, общее для всех предметов[7]:
Исследования в этой области ведутся сейчас и другими представителями педагогической науки. Но сегодня под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению. Проблемное обучение строится на основе принципа проблемности, реализуемого через различные типы учебных проблем и через сочетание репродуктивной, продуктивной и творческой деятельности ученика. Наличие различных типов учебных проблем обеспечивает поисковую, или частично-поисковую, или конструкторско-изобретательскую деятельность ученика, или их сочетание в ходе выполнения теоретических и практических самостоятельных работ, при изложении учебного материала учителем на уроке. Цель педагогической деятельности автора работы – адаптировать методы и приемы проблемного обучения в преподавании математики, а также разработать систему заданий, которая помогла бы сформировать у учащихся те навыки и воспитать те качества, о которых говорилось выше. Для достижения поставленной цели автор придерживается теории М.И. Махмутова и А. М. Матюшкина, которая, по его мнению, наиболее близка в реализации технологии проблемного обучения в современном образовательном процессе.
Новизна опыта заключается в комбинации технологий: технологии проблемного обучения, в создании системы методов и приемов, нацеленных на развитие познавательной активности при изучении математики и творческих способностей учащихся. Раздел II Технология опыта Целью педагогического опыта является развитие познавательной активности школьников на основе проблемного обучения, и как следствие - повышение качества знаний учащихся по математике. Для достижения поставленной цели считаю необходимым решение следующих задач: 1) использование на уроках технологии проблемного обучения, что позволяет научить детей мыслить логически, научно, творчески; сделать учебный материал более доказательным и убедительным для учащихся; формировать не просто знания, а знания-убеждения, что служит основой для формирования научного мировоззрения; 2) введение в педагогическую практику такой организации образовательного процесса, которая содействовала бы формированию прочных знаний на основе самостоятельно добытых учащимися сведений, воздействовала бы на эмоциональное состояние школьников, формируя такие чувства, как уверенность в своих силах, удовлетворение от умственной деятельности; 3) использование методов, способов и приемов, направленных на обеспечение оптимального процесса обучения и развития познавательной активности школьников, формирование элементарных навыков поисковой и исследовательской деятельности, развитие положительного отношения, интереса, как к данному учебному предмету, так и к учению вообще. Эти задачи могут быть реализованы с большим успехом именно в процессе проблемного обучения, поскольку усвоение учебного материала происходит в ходе активной поисковой деятельности учащихся, в процессе решения ими системы проблемно-познавательных задач. Проблемное обучение существенно отличается от традиционного. При проблемном обучении учитель либо не даёт готовых знаний, либо даёт их на особом предметном содержании – новые знания, умения и навыки школьники приобретают самостоятельно при решении особого рода задач и вопросов, называемых проблемными. При традиционном обучении упор делается на мотивы непосредственного побуждения (учитель интересно рассказывает, показывает), при проблемном же обучении ведущими мотивами познавательной деятельности становятся интеллектуальные (учащиеся самостоятельно ищут знания, испытывая удовлетворение от процесса интеллектуального труда, от преодоления сложностей и найденных решений, догадок, озарений). Учебный процесс в условиях проблемного обучения имеет следующую структуру:
На уроке, проводимом по технологии проблемного обучения, соблюдаются следующие этапы: - мотивация, создание проблемной ситуации; - выдвижение гипотез и их запись на доске; - исследование (теоретическое, практическое); - обмен информацией при работе в группах, парах, представление работы; - обработка информации (выделение значимой информации, подтверждение или опровержение высказанных ранее гипотез); - подведение итогов урока, рассмотрение новых вариантов решения проблемы; - домашнее задание; - рефлексия. Существует несколько критериев, позволяющих оценить работу учащихся на таком уроке:
Автор опыта считает, что данная структура урока в наибольшей степени развивает навыки самостоятельной работы, обеспечивает повышение познавательной и социальной мотивации учащихся, формирует умения применять ранее усвоенные знания в новой ситуации, творчески их преобразовывать, способствует развитию интеллектуальных способностей школьников. Самообучение, создание проблемных ситуаций, их анализ, активное участие учеников в поиске путей решения поставленной учебной проблемы возбуждает мыслительную активность учащихся, поддерживает глубокий познавательный интерес. В своей работе автор использует разнообразные методы и приемы работы: работа по алгоритму, самостоятельная работа с учебником, работа в парах переменного состава, работа по тестам, фронтальная работа, работа в группах, индивидуальная работа, взаимопроверка, самопроверка, дифференцированное домашнее задание, специальные задания, памятки по работе, тренировочные упражнения. А так же разнообразные формы организации урока: традиционный урок, урок-путешествие (приложение 1), урок-исследование, урок-практикум, деловые игры. Организует учебный процесс по принципу проблемности, чтобы отношение учащихся к возникающим проблемным ситуациям было вдумчивым и осмысленным. Целенаправленное использование учителем проблемных ситуаций, возникающих помимо его желания (объективно), и ситуаций, преднамеренно им создаваемых, представляют собой систему, умелое применение которой и является основной особенностью проблемного обучения и его отличием от традиционного. Пример1, являющийся иллюстрацией постановки проблемной ситуации с целью установления новой важной связи между сложением и умножением чисел в пятом классе при изучении темы «Распределительный закон умножения относительно сложения». На данном уроке учащимся предлагается решить двумя способами следующие задачи: Задача 1. В школьном саду посажены фруктовые деревья в 10 рядов. В каждом ряду посажено по 5 груш и по 7 яблонь. Сколько всего деревьев посажено в саду? Решение. 1 способ. 2 способ. (7 + 5) * 10 = 120 7 * 10 + 5 * 10 = 120 Ответ: 120 деревьев. Задача 2. Две автомашины одновременно выехали навстречу друг другу из двух пунктов. Скорость первой автомашины 80 км в час, скорость второй 60 км в час. Через 3 часа автомашины встретились. Какое расстояние между пунктами, из которых выехали автомашины? Решение. 1 способ. 2 способ. (80 + 60) * 3 = 420 80 * 3 + 60 * 3 = 420 Ответ: 420 км З 4м 2м 3м  адача 3. Задача 3. Найти площадь прямоугольного участка, состоящего из двух прямоугольных участков. адача 3. Задача 3. Найти площадь прямоугольного участка, состоящего из двух прямоугольных участков. 1 способ. 2 способ. (4 + 2) * 3 = 18 4 * 3 + 2 * 3 = 18 Ответ: 18 м После решения всех трёх задач учащимся предлагается самостоятельно сравнить: а) первые способы решения задач; б) вторые способы решения задач; в) выражения, полученные при решении задач 1-м (2-м) способом; г) выражения, полученные при решении задачи № 1 (№ 2, № 3) и 1 и 2-мя способами; д) числовые значения выражений, полученные при решении задачи № 1 (№ 2, № 3) 1-м и 2-м способами. В результате такого сравнения учащиеся пришли к следующим выводам: 1-й способ решения всех задач одинаков, 2-й – тоже; выражения, полученные при решении задач 1-м (2-м) способом, отличаются друг от друга только числовыми данными; выражения, полученные при решении задачи №1 (№ 2, № 3) 1-м и 2-м способами, отличаются друг от друга числом арифметических действий и порядком действий; числовые значения выражений, полученные при решении задачи №1 (№ 2, № 3) 2-мя способами, одинаковы, а, значит, можно сделать такую запись: (7 + 5) * 8 = 7 *8 + 5 * 8. (80 + 60) * 3 = 80 * 3 + 60 * 3. (5 + 3) * 4 = 5 * 4 + 3 * 4. Далее предлагается ученикам заменить одинаковые цифры в полученных выражениях одинаковыми буквами. В результате получены три одинаковых выражения, а именно: (а + в) * с = ас + вс. Потом учитель говорит: - Из трёх различных числовых выражений получились три одинаковых буквенных выражений. Встречались ли вы с таким явлением? - Встречались, - отвечают ученики, - например, при записи переместительного закона умножения. - И в этом случае, - продолжает учитель, - мы получили новый закон умножения: распределительный закон умножения относительно сложения. Ученики с помощью учителя формулируют этот закон словесно и на примерах убеждаются в целесообразности усвоения и запоминания этого закона: он облегчает вычисления. Пример 2, где при решении проблемной ситуации учащимся необходимо: выдвижение гипотез, формулировка выводов и их опытная проверка. «Признаки делимости чисел на 10, на 5 и на 2» (Математика, 5 класс). На доске записаны числа: 1 289 565, 246 560, 24, 188 536, 1873. Ученикам предлагается найти среди этих чисел те, которые делятся на 10, на 5 и на 2, не производя деления; написать несколько многозначных чисел, делимость которых на 10, на 5 и на 2 они могут предугадать; попытаться найти признаки делимости чисел на 10, на 5 и на 2. Высказать своё мнение: стоит ли этим заниматься? Не проще ли разделить? Разрешается обсуждение с соседом или в группе. После высказывания предположений ученики проверяют их непосредственным делением. Затем идет сопоставление с учебником, и формулируются окончательные выводы. Пример 3, побуждающий учащихся к предварительному обобщению новых фактов. Учащиеся получают задания: рассмотреть некоторые факты, явления, содержащиеся в новом для них материале, сравнить их с известными, и сделать самостоятельное обобщение. «Функция у=ах2, её графики свойства». (Алгебра 9 класс) Учащимся предлагается построить попарно графики функций у=2х2 и у= -2х2и, опираясь на непосредственное изображение графиков, заполнить таблицу:
После заполнения таблицы учащиеся делают окончательные выводы и формулируют основные свойства. Пример 4. Побуждение учащихся к предварительному обобщению новых фактов. Учащиеся получают задания рассмотреть некоторые факты, явления, содержащиеся в новом для них материале, и на основе сравнения и анализ сделать выводы и заключения.. «Формулы сокращённого умножения» (Алгебра 7 класс) При изучении темы учитель предлагает ученикам решить ряд примеров, ранее известным им способом умножением многочлена на многочлен. Одновременно с учениками учитель решает эти примеры, записывая решение так, чтобы ученики не видели, а затем предлагает проверить решение и записи.
Ученики, сравнивая ответы и записи решений, видят, что запись решения, сделанная учителем короче, но при этом ответы одинаковые. И тут учитель предлагает учащимся найти некоторые закономерности, которые потом формулируются в правило. Особое внимание учеников при изучении темы «Формулы сокращённого умножения» обращается на то, что знание формул широко используется в заданиях. ЕГЭ и ГИА. (приложение ) Пример 5, использование ситуаций, возникающих при выполнении учащимися практических заданий. Проблемная ситуация в этом случае возникают при попытке учащихся самостоятельно достигнуть поставленной перед ними практической цели «Площадь круга» (Геометрия 9 класс) Объяснение нового материала целесообразно начать с того, что постепенно ввести учащихся в проблемную ситуацию. Учащимся предлагается описать около окружности радиуса r квадрат, отметить точки касания этого квадрата с окружностью, через эти точки провести перпендикулярные диаметры, в результате получается фигура – тоже квадрат. Требуется найти, у какой из этих 3-х фигур (2-х квадратов и круга) площадь наибольшая, у какой – наименьшая. Учащиеся быстро отвечают, что площадь круга меньше площади описанного квадрата, но больше площади вписанного квадрата, то есть 2 r2 < s кр. < 4 r2 . Обозначив площадь круга через k * r2, легко получить, что 2 r2 Проблемный характер изложения учебного материала, организация поисковой, познавательной деятельности учащихся, даёт им возможность переживать радость самостоятельных открытий. При таком ведении урока повышается активность учащихся, их заинтересованность в результатах урока. Использование проблемных ситуаций, исследовательских заданий, частично - поискового метода обучения позволяет организовать работу на уроке с субъектным опытом учащегося, не просто излагать свой предмет, а анализировать содержание, которым располагают ученики по теме урока. Раздел III Результативность опыта Использование проблемного метода обучения позволило получить следующие результаты:
Об этом свидетельствуют результаты проведение диагностик: - по определению внешней и внутренней мотивации учебной деятельности учащихся:
- по изучение уровня познавательной активности ( опросник Ч.Д. Спилбергера (модификация А.Д.Андреевой,1987год))
- позитивная динамика учебных достижений учащихся одного и того же класса за 3 года 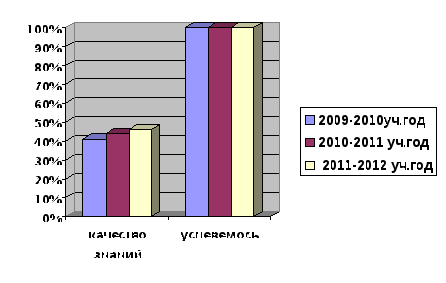 Таким образом, результативность деятельности по обеспечению положительной динамики уровня познавательной активности в учебно-воспитательном процессе достигнута посредством использования технологии проблемного обучения при изучении математики. Исходя из этого, можно сделать вывод о перспективности дальнейшего использования технологии проблемного обучения с целью достижения более высокого уровня сформированности познавательной активности учащихся при изучении математики. Библиографический список:
М. Педагогика 1972.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||