Использование технологии проблемного диалога на уроках математики как средство формирования познавательных универсальных учебных действий

Название	Использование технологии проблемного диалога на уроках математики как средство формирования познавательных универсальных учебных действий
Дата	27.02.2016
Размер	80.8 Kb.
Тип	Реферат

Использование технологии проблемного диалога на уроках математики как средство формирования познавательных универсальных учебных действий.
Красноперова Л.А., учитель математики

МБОУ «Гимназия №22»г. Белгорода
Модернизация современного образования ставит перед общеобразовательной школой новые задачи: формирования опыта самостоятельной деятельности учащихся и формирование целостной системы универсальных учебных действий.

На мой взгляд, проблема развития познавательной активности учащихся в условиях современной школы, формирование у них познавательных универсальных учебных действий имеет очень большое значение.

Считаю, что содержание учебного материала, традиционные методы обучения и формы организации учебного процесса не способствуют в полной мере динамичному развитию школьников в соответствии с современными требованиями. Таким образом, обнаруживается противоречие между необходимостью формирования у учащихся познавательных универсальных учебных действий и недостаточной технологической проработкой этого процесса в условиях традиционного обучения.

Для решения этой проблемы пришла к необходимости использования современных образовательных технологий на уроках математики. В течение двух лет в своей педагогической деятельности я использовала технологию проблемного обучения. В связи с введением новых образовательных стандартов в основной школе, переходом на образовательную систему «Школа-2100» начала осваивать новые технологии: технологию проблемного диалога и технологию оценки учебных успехов учащихся.

Технология проблемного-диалога дает развернутый ответ на вопрос, как учить, чтобы ученики ставили и решали проблемы. В словосочетании «проблемный диалог» первое слово означает, что на уроке изучения нового материала должны быть проработаны два звена: постановка учебной проблемы и поиск ее решения: постановка проблемы – это этап формулирования темы урока или вопроса для исследования; поиск решения – этап формулирования нового знания.

Слово «диалог» означает, что постановку проблемы и поиск решения ученики осуществляют в ходе специально выстроенного учителем диалога.

Различают два вида диалога: побуждающий и подводящий.

Побуждающий диалог состоит из отдельных стимулирующих реплик, которые помогают ученику работать по-настоящему творчески. На этапе постановки проблемы этот диалог применяется для того, чтобы ученики осознали противоречие, заложенное в проблемной ситуации, и сформулировали проблему. На этапе поиска решения учитель побуждает учеников выдвинуть и проверить гипотезы, т.е. обеспечивает «открытие» знаний путем проб и ошибок.
Подводящий диалог представляет собой систему вопросов и заданий, которая активизирует и, соответственно, развивает логическое мышление учеников. На этапе постановки проблемы учитель пошагово подводит учеников к формулированию темы. На этапе поиска решения он выстраивает логическую цепочку умозаключений, ведущих к новому знанию.

Учитель сначала в диалоге помогает ученикам поставить учебную проблему, т.е. сформулировать тему урока или вопрос для исследования, тем самым, вызывая у школьников интерес к новому материалу, формируя познавательную мотивацию.

Затем посредством одного из диалогов учитель организует поиск решения, или «открытие» нового знания. При этом достигается подлинное понимание учениками материала, ибо нельзя не понимать то, до чего додумался сам.

При использовании технологии проблемного диалога учитель не даёт готовых знаний – новые знания, умения и навыки школьники приобретают самостоятельно при решении особого рода задач и вопросов, называемых проблемными. Учащиеся самостоятельно ищут знания, испытывая удовлетворение от процесса интеллектуального труда, от преодоления сложностей и найденных решений, догадок, озарений.

Таким образом, технология проблемного диалога– это технология, обеспечивающая творческое усвоение знаний учащимися посредством специально организованного учителем диалога.

Поэтому перед собой, как педагогом, определила следующие цели - адаптировать методы и приемы технологии проблемного диалога в преподавании математики, а также начать разработку системы заданий, которые помогли бы формировать у учащихся познавательные универсальные учебные действия: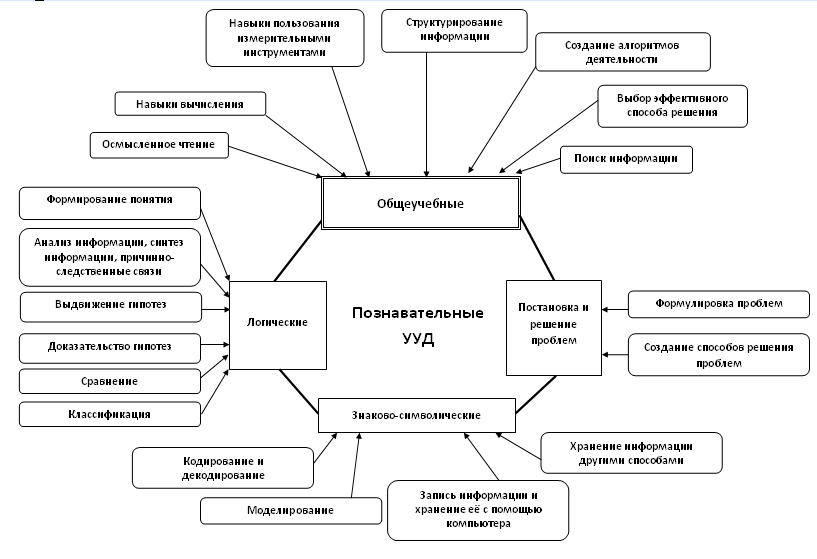

Для достижения поставленной цели считаю необходимым решение следующих задач:

научить детей мыслить логически, научно, творчески; сделать учебный материал более доказательным и убедительным для учащихся;
вводить в свою практику формы организации образовательного процесса, которые содействовали бы формированию прочных знаний на основе самостоятельно добытых учащимися сведений;
использовать методы, способы и приемы, направленные на обеспечение развития познавательной активности школьников, формирование элементарных навыков поисковой и исследовательской деятельности,

В своей практике на уроках математики начала использовать различные задания, которые позволяют организовать диалог.

Например: при изучении темы «Распределительный закон умножения относительно сложения» с целью установления новой важной связи между сложением и умножением чисел предлагаю учащимся решить следующие задачи двумя способами:

Задача 1. В школьном саду посажены фруктовые деревья в 10 рядов. В каждом ряду посажено по 5 груш и по 7 яблонь. Сколько всего деревьев посажено в саду?

Решение.

1 способ. 2 способ.

(7 + 5) · 10 = 120 7 · 10 + 5 · 10 = 120

Ответ: 120 деревьев.

Задача 2. Две автомашины одновременно выехали навстречу друг другу из двух пунктов. Скорость первой автомашины 80 км в час, скорость второй 60 км в час. Через 3 часа автомашины встретились. Какое расстояние между пунктами, из которых выехали автомашины?

Решение.

1 способ. 2 способ.

(80 + 60) · 3 = 420 80 ·3 + 60 · 3 = 420

Ответ: 420 км

З
7м 2м

5м
адача 3. Найти площадь прямоугольного участка, состоящего из двух прямоугольных участков.

1 способ. 2 способ.

(7 + 2) · 5 = 45 7 · 5 + 2 · 5 = 45 Ответ: 45 м

Организовать работу можно как в группе, в парах, так и индивидуально, все это зависит от класса.

После решения всех трёх задач учащимся предлагаю самостоятельно сравнить:

а) первые способы решения задач;

б) вторые способы решения задач;

в) выражения, полученные при решении все трех задач первым способом и вторым способом;

г) выражения, которые были получены при решении конкретной задачи (например, задачи №1);

В результате такого сравнения учащиеся пришли к следующим выводам:

1-й способ решения всех задач одинаков, 2-й – тоже; выражения, полученные при решении задач 1-м (2-м) способом, отличаются друг от друга только числовыми данными. Выражения, полученные при решении задачи №1 (№ 2, № 3) 1-м и 2-м способами, отличаются друг от друга числом арифметических действий и порядком действий; числовые значения выражений, полученные при решении задачи №1 (№ 2, № 3) 2-мя способами, одинаковы, а, значит, можно сделать такую запись:

(7 + 5) · 8 = 7 ·8 + 5 · 8.

(80 + 60) · 3 = 80 · 3 + 60 · 3.

(5 + 3) · 4 = 5 ·4 + 3 · 4.

Далее предлагаю учащимся заменить одинаковые цифры в полученных выражениях одинаковыми буквами. В результате получены три одинаковых выражения, а именно:

(а + в) · с = ас + вс.

Потом я говорю:

- Из трёх различных числовых выражений получились три одинаковых буквенных выражения. Встречались ли вы с таким явлением?

- Встречались, - отвечают ученики, - например, при записи переместительного закона умножения.

- И в этом случае, - продолжаю я, - мы получили новый закон умножения: распределительный закон умножения относительно сложения.

Ученики с моей помощью формулируют этот закон словесно и на примерах убеждаются в целесообразности усвоения и запоминания этого закона: он облегчает вычисления.

При работе над этими задачами мною был организован подводящий диалог.

Какие же познавательные универсальные учебные действия формируются при выполнении данного задания? Это, прежде всего, анализ текстов задачи; структурирование информации в тексте задачи; определение способов решения задачи; сравнение; обобщение; перевод из одной знаковой системы в другую (из числового выражения в буквенное).

Возьмем другой пример. При изучении темы «Признаки делимости чисел на 10, на 5 и на 2» для решения проблемной ситуации учащимся необходимо было выдвинуть гипотезу, проверить её и сформулировать выводы.

На доске записаны числа: 1 289 565, 246 560, 24, 188 536, 1873. Предлагаю учащимся, не производя деления, из предложенных чисел, найти те, которые делятся на 10, на 5 и на 2.

Затем предлагаю самостоятельно написать несколько многозначных чисел, делимость которых на 10, на 5 и на 2 они могут предугадать.

После того как, учащиеся выполнят эту работу, я предлагаю им попытаться найти признаки делимости чисел на 10, на 5 и на 2.

После того как учащиеся попытаются сформулировать признаки, предлагаю им высказать своё мнение: стоит ли этим заниматься? Не проще ли разделить?

После высказывания предположений ученики проверяют их непосредственным делением. Затем организуется сопоставление с учебником, и формулируются окончательные выводы, которые записываются в форме таблицы:

Признаки делимости натуральных чисел
Если оканчиваются	На 10	На 5	На 2
Если оканчиваются	0	0 или 5	0; 2; 4;5; 6 ;8

При работе над этими задачами мною был организован побуждающий диалог.

Какие же познавательные универсальные учебные действия формируются при выполнении данного задания? Это, прежде всего, анализ предложенной информации; выдвижение гипотезы, доказательство гипотезы; структурирование информации; поиск информации в учебнике (справочниках).

Проблемный характер изложения учебного материала, организация поисковой, познавательной деятельности учащихся, даёт им возможность переживать радость самостоятельных открытий, формирует универсальные учебные действия.