Функции, их свойства и графики. Определение функции

• Функции, их свойства и графики.

Определение функции.

• Среди перечисленных ниже зависимостей укажите только те, которые представляют собой функцию:

• у = х2 + 1, y = 8, x = - 1, y = |x|,

• Дайте определение функции.

Область определения и область значений функции.

• Укажите область определения функций:

• Для функций, записанных выше, укажите область значений.

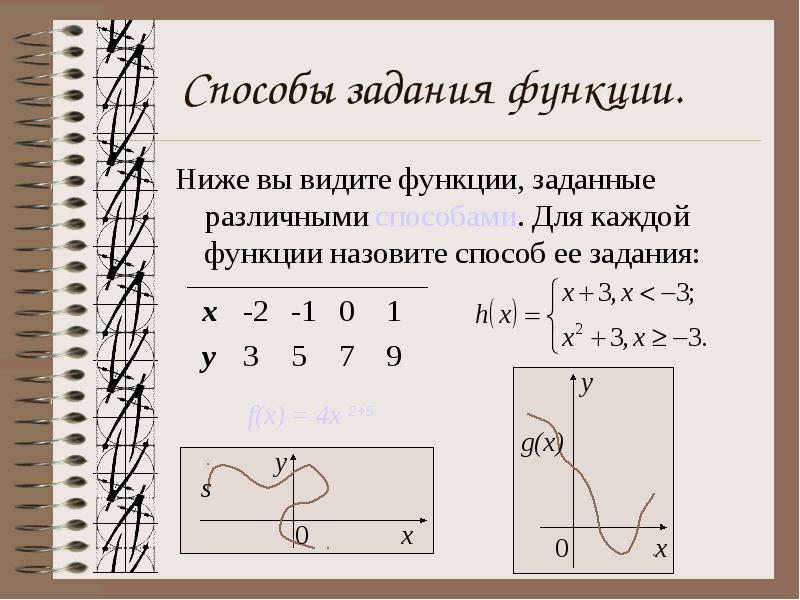
Способы задания функции.

• Ниже вы видите функции, заданные различными способами. Для каждой функции назовите способ ее задания:

Виды функций.

• Были изучены следующие виды функций:

• линейная;

• прямая и обратная пропорциональность;

• дробно-линейная;

• квадратичная;

• y = |x|;

• y = [x], y = {x}, y = sgn x.

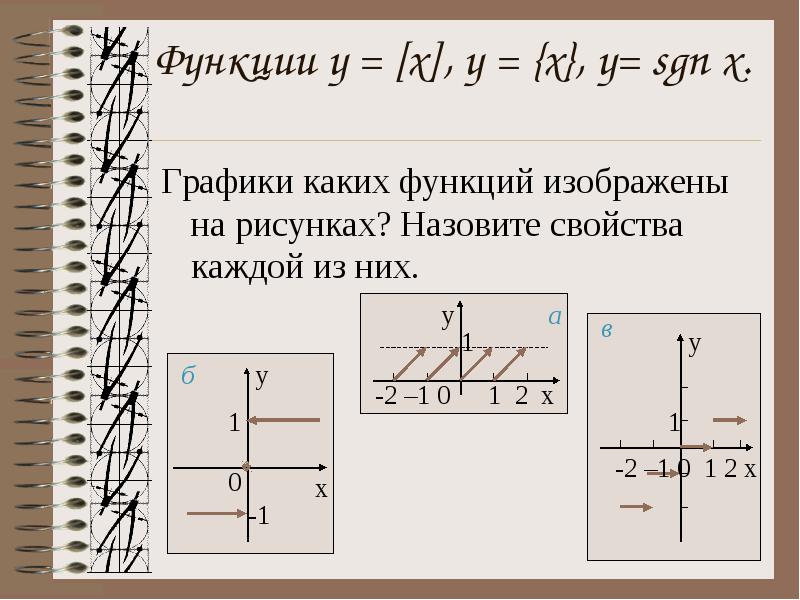
Функции у = [x], y = {x}, y= sgn x.

• Графики каких функций изображены на рисунках? Назовите свойства каждой из них.

Выводы.

• Итак, в результате работы над проектом мы изучили свойства и построили графики следующих функций:

• линейной;

• прямой и обратной пропорциональности;

• дробно-линейной;

• квадратичной;

• y = |x|;

• y = [x], y = {x}, y = sgn x.

Самостоятельная работа.

• Самостоятельная работа состоит из двух частей:

• компьютерный тест;

• письменная работа по карточкам.

• Функцией называется зависимость одной переменной от другой, при которой каждому значению независимой переменной ставится в соответствие единственное значение зависимой переменной.

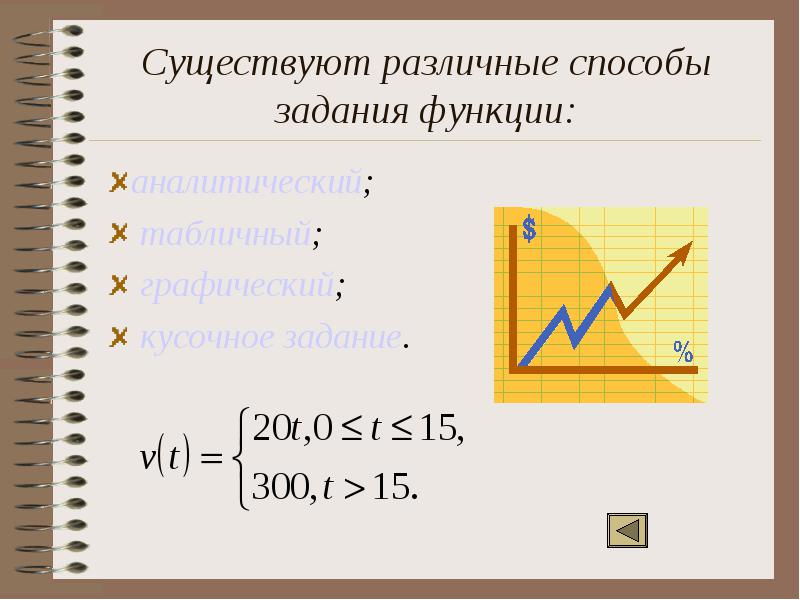
Существуют различные способы задания функции:

• аналитический;

• табличный;

• графический;

• кусочное задание.

Аналитический способ задания функции.

• Задание функции с помощью формулы (аналитического выражения) называют аналитическим способом задания функции.

Табличный способ задания функции.

• Функцию можно задать таблицей, где перечисляются все значения аргумента и функции. Такой способ задания функции называется табличным.

Графический способ задания функции.

• Задание функции с помощью графика называется графическим способом.

• Графиком функции у = f (х) называется множество точек (х, у), координаты которых удовлетворяют данному уравнению.

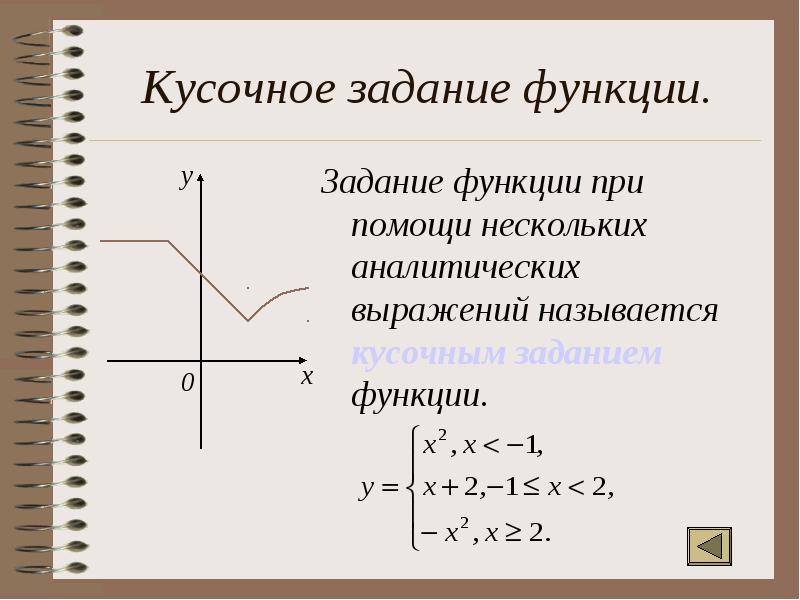
Кусочное задание функции.

• Задание функции при помощи нескольких аналитических выражений называется кусочным заданием функции.

• Множество всех значений аргумента, при которых данная функция принимает числовое значение, называют областью определения этой функции.

• Множество всех значений функции, которые она принимает при допустимых значениях аргумента, называют областью значений функции.

• а – функция y = {x}; D(y) = R, E(y) =[0; 1).

• б – функция y = sgn x;

• D(y) = R, E(y) = {-1; 0; 1}.

• в – функция y = [x];

• D(y) = R, E(y) = Z.