Задачи урока. Образовательная
 Скачать 60.09 Kb. Скачать 60.09 Kb.
|
               Решение логарифмических уравнений Цель урока. 1. Формирование умения решать логарифмические уравнения с использованием свойств логарифмов и общих методов решения уравнений. Задачи урока. Образовательная. Создать условия для отработки общих подходов к решению логарифмических уравнений Развивающая. Способствовать развитию математического языка, коммуникативных умений учащихся Воспитательная. Воспитание активности, умения общаться, общей культуре. Помочь учащимся осознать ценность коллективной деятельности. Ход урока I этап – Мотивационно – ориентировочный. Организационный момент (приветствие, психологический настрой на работу, постановка целей и задач урока). II этап -Актуализация знаний. Устная работа. III этап – основной. Работа над углублением материала темы «Логарифмические уравнения». IV этап - Подведение итога урока. Домашнее задание. Ход урока I этап. Организационный момент. -Здравствуйте, ребята! -На предыдущем уроке мы с вами приступили к решению логарифмических уравнений, рассмотрели методы их решений. Сегодня мы продолжим работу над решением различных логарифмических уравнений. -Откройте тетради, запишите число и тему урока: «Решение логарифмических уравнений». II этап. Анализ затруднений при выполнении домашнего задания. Устная работа. А) -Какие уравнения называются логарифмическими? (в которых переменная находится под знаком логарифма) -Выберите среди предложенных уравнений логарифмические . 1. 3x2 + 6x – 8 = 0 2. (x + 3)3 +2(x +3) = 0 3. log5(3x – 2) = 3 4. 2log2 x + log 215 = log2 (x + 6) 5. y = log3 (3x – 8) 6. 7х+5 = 49 7. 2log2 3 x – 5log3 x + 2 = 0 Б)- Всегда ли логарифмическое уравнение решаемо, т.е. имеет смысл? (Вспомним ОДЗ логарифмической функции) Назовите номера логарифмических уравнений, которые не имеют смысла. 1. log3 x = - 2 2. log1 x = log15 3. log-2x = - 5 4. log3 2x + log3x + 6 = 0 5. log16x + log8x = log3x 6. log3(-5) + log3x = log3(2x +5) В) – С какими основными методами решения логарифмических уравнений мы познакомились?
Г)- Определите метод решения каждого уравнения : 1. lg(x + 3) = 2lg2 + lgx 2. log2x – 2logx2 = -1 3. log42x – log4x – 2 = 0 4. xlgx + 2 = 100x 5. logx-6(x2 – 5) = logx-6(2x + 19) 6. x log3 x = 81 7. lgx=11 - x III этап - Основной. Работа над углублением материала темы «Логарифмические уравнения». Учитель предлагает учащимся решить уравнения по тренажеру . Каждое из предложенных уравнений решают ученики на доске, выходя к доске по желанию или по просьбе учителя. Остальные работают в тетрадях. Учитель ходит по классу, помогает учащимся в случае необходимости, проверяет решенные уравнения. Решить уравнения: 1. Log1/3x log1/3 (3x-2)= log1/3 (3x-2) Решение. Д(у): х > 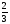 Log1/3x log1/3 (3x-2)= log1/3 (3x-2) Log1/3x log1/3 (3x-2) - log1/3 (3x-2)=0 Log1/3 (3x-2) ( log1/3 х-1)=0 Log1/3 (3x-2) =0 log1/3 х-1=0 3х-2=1 х = 1 log1/3x=1 х = 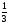 Ответ: 1.
Решение: Д(у) : - 1 < x < 3 Log5(1 + x) + log5(3-x) – log5(1 + x) = log52 3 – x = 2 X = 1. Ответ: 1
Д(у): х > 0 x ≠ 1 x ≠ 0,5 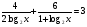 . Пусть log2x = t. . Пусть log2x = t.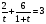 ; 3t2 - 5t – 2 = 0; ; 3t2 - 5t – 2 = 0;t = 2 log2x = 2 x = 4 t = 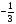 ; log2x = ; log2x = 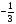 ; x = ; x = 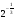 Ответ: 4; 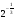 . .4. Log2(3x+1) log3x=2 log2(3x+1) Решение: Д(у) : х > 0 Log2(3x+1)log3x-2log2(3x+1)=0; Log2(3x+1)(log3x -2)=0; Log2(3x+1)=0 или log3x=2 3x+1=1; или x=32; 3x=0 или x=9 x=0- посторонний корень. Ответ: 9. 5. Log 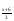 (log2 (log2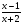 ) = 0 ) = 0Решение: Д(у): - 6 < x < - 2; x > 1. log2 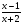 = 1; = 1;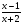 = 2; = 2;х – 1 = 2х + 4; х = -5. Ответ: - 5.
Решение : Д(у): х > 0, х ≠ 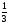 . .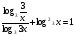 ; ;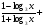 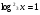 ; ;Пусть log3x = t, t≠ - 1. Тогда 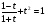 . .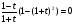 ; ;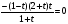 ; ; t= 0 log3x = 0 x = 1 t = 1 log3x = 1 x = 3 t = -2; log3x = - 2; x = 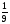 . .Ответ: 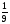 ; 1; 3. ; 1; 3.7. 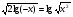 Решение: Д(у): х 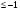 ; ; Пусть lg(-x) = t, t 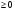 . .Тогда: 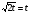 ; ; 2t = t2; t = 0 lg( - x) = 0 x = - 1 t = 2; lg ( - x) = 2; x = - 100. Ответ: - 100; - 1.
Решение: Д(у): х > 0; х ≠ 1. 3х2·0,5logxx = х + 4 1,5 х2 - х – 4 = 0 х = 2 , т.к. 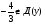 . .Ответ: 2 9. 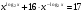 Решение: Д(у): х > 0. Пусть 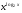 = t, t > 0. = t, t > 0.Тогда 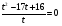 t = 1 или t = 16; 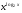 =1 или =1 или 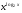 = 16; = 16;log2 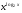 = log21 или log2 = log21 или log2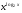 = log2 16; = log2 16;log2 2x = 0 или log2 2x = 4; x = 1 или х = 4 х = 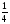 Ответ: 0,25; 1; 4.
Решение: Д(у) : х > 0. 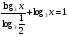 ; ;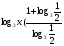 ) = 1; ) = 1;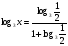 ; т.к. 1 + ; т.к. 1 + 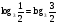 , тогда , тогда 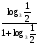 = = 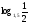 ; ;Х = 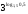 Ответ: 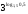 IV этап - Подведение итога урока. Учитель благодарит учащихся за работу на уроке, тем, кто выполнил не менее пяти заданий правильно– выставляет отметку «пять» в журнал, тем, кто ошибся - «4» или «3», но отметка не выставляется, если ученика она не устраивает. Домашнее задание.
|
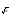 (1+х) = log0,2(0,5)
(1+х) = log0,2(0,5)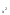 16 + log2x64 = 3
16 + log2x64 = 3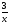 + log2 3x = 1
+ log2 3x = 1