Урок по математике по теме «Задачи на движение. 5 Класс». Урок повторение по теме «Движение»
 Скачать 94.75 Kb. Скачать 94.75 Kb.
|
| Урок по математике по теме «Задачи на движение. 5 Класс». Урок - повторение по теме «Движение» (рассчитан на сдвоенный урок). Цель урока: обобщение изученного материала с помощью решения задач на движение:
Задачи:
1. В устной форме проговариваются основные величины от которых зависит движение. Скорость V и время t. Единицы измерения: V (м,км…) и t (с,ч,мин). Повторяем формулы 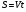 , , 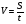 , , 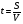 . .На доске заранее составляется таблица. Учитель предлагает ученикам заполнить пустые ячейки: №/№ S V t 1 7,5 км ? 0,3 ч 2 6 м 50 м/с ? ------------------------------------------------------------------------------------------------------------- 3 0,12 км ? м/с 0,04 ч В задаче 3 обратить внимание учащихся на единицы измерения скорости V (м/с), следует предварительно перевезти S в метры и t в секунды. Учащимся предлагается вспомнить определение средней скорости и формулы: 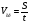 , где S – весь путь, а t – всё время. , где S – весь путь, а t – всё время.Задача (из сборника для подготовки к ГИА ): Условие задачи: Первую половину трассы автомобиль проехал со скоростью 42 км/ч, а вторую половину – 63 км/ч. Найти среднюю скорость автомобиля на протяжении всего пути. Анализ задачи:
1 П. трассы – 42 км/ч 2 П. трассы – 63 км/ч Ср. скорость - ? км/ч
Решение (алгебраический способ): Пусть время в пути – Х часов. Тогда, первая половина трассы составит 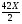 км, а вторая половина трассы – км, а вторая половина трассы – 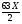 ) км. По формуле найдём среднюю скорость: ) км. По формуле найдём среднюю скорость: 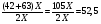 (км/ч). (км/ч).
№1 Задача на движение в одном направлении: Условие задачи: Турист на велосипеде проехал всего 18,5 км, проезжая в час по 22 км по асфальтовой дороге и 15 км по грунтовой. По асфальтовой дороге турист ехал столько же времени сколько и по грунтовой. Сколько километров турист проехал по асфальтовой и сколько по грунтовой дорогам? Анализ задачи:
Вид дороги V t S Асфальтовая 22 км/ч Всего Грунтовая 15 км/ч 18,5 км Решение (арифметический способ):
Учащимся предлагается рассмотреть и другой способ решения. Решение (алгебраический способ): Пусть Х – время движения по каждому участку. Тогда, 22Х (км) путь по асфальтовой дороге и 15Х (км) – по грунтовой дороге. Составим и решим уравнения:
37Х = 18,5 Х = 0,5.
Ответ: 11 км и 7,5 км. №2 Задача на движение в одном направлении: Условие задачи: Из двух городов выехали одновременно велосипедист со скоростью 27 км/ч и мотоциклист со скоростью 41 км/ч. Сколько часов они были в пути мотоциклист проехал больше велосипедиста на 9,8 км? Анализ задачи:
V t S Велосипедист 27 км/ч ? ч Мотоциклист 41 км/ч ? ч на 9,8 км больше Выехали одновременно. Решение (алгебраический способ): Пусть Х – время движения каждого. Тогда, путь велосипедиста составит 27Х (км), а мотоциклиста – 41Х (км). Мотоциклист проехал на 9,8 (км) больше, следовательно эта разница. Составим и решим уравнение: 41Х – 27Х = 9,8 14Х = 9,8 Х = 0,7 (ч). Учащимся предлагается рассмотреть и другой способ решения. Решение (арифметический способ): 9,8 (км) – расстояние, на которое мотоциклист проехал больше велосипедиста за то же время. Найдём разницу скоростей: 41 – 27 = 14 (км/ч) Тогда, 9,8 : 14 = 0,7 (ч) – время проведённое в пути каждым. Ответ: время проведённое в пути составляет 0,7 часа. Физкультминутка. Поднимает руки класс – это «раз». Повернулась голова – это «два». Руки вниз, вперёд смотри – это «три». Руки в стороны пошире развернули на «четыре». С силой их к плечам прижать – это «пять». Всем ребятам нужно сесть – это «шесть». №3 Задача на движение в разных направлениях: Условие задачи: Мотоциклист и велосипедист выехали в разных направлениях. Велосипедист ехал несколько часов со скоростью 2,4 (км/ч). С какой скоростью ехал мотоциклист, если расстояние в 6 раз большее он проехал за время в 3 раза меньшее, чем велосипедист? Анализ задачи:
V t S Велосипедист 2,4 км/ч Мотоциклист ? км/ч ,расстояние в 6 раз больше проехал за время в 3 раза меньшее Решение (алгебраическим способом): Пусть время велосипедиста Х часов. Тогда, пройденный им путь составит 2,4Х (км). Мотоциклист проехал в 6 раз больше, т.е. 2,4Х * 6 (км) за время Х/3 (ч). Найдём скорость мотоциклиста 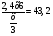 (км/ч). (км/ч).Ответ: скорость мотоциклиста 43,2 (км/ч). №4 Задачи на движение по реке и озеру: Учитель с учениками вспоминают особенности задач на движение по реке: Скорость по течению = скорость собственная + скорость течения . Скорость против течения = скорость собственная – скорость течения. Скорость движения по озеру = скорость собственная. Условие задачи: Задача №1: Скорость лодки против течения реки 22,3 (км/ч). Найдите скорость течения реки, если за 4 (ч) по озеру она прошла 104,8 (км)? За сколько времени лодка преодолеет такое же расстояние двигаясь по течению реки? Анализ условия: Вид движения V t S По озеру 4 (ч) 104,8 (км) Против течения 22,4 (км/ч) Вопрос 1: Найти скорость течения: Решение (арифметический способ):
Вопрос 2: Найти время при движении по течению реки:
Ответ: 3,8 (км/ч) и 3,16 (ч). Условие задачи: Задача №2: Катер шёл 5 часов по течению реки и прошёл 150 километров. Сколько времени ему понадобится на обратный путь, если скорость течения реки 2,5 км/ч? Ответ округлить до десятых. Анализ условия: Вид движения V t S По течению 5 (ч) 150 (км) Против течения ? (ч) 150 (км) Скорость течения реки 2,5 (км/ч). Решение (арифметический способ):
Ответ: 2,5 (км/ч); 5,5 (ч). Физкультминутка. - Встали. Закрыли глаза. Вспомнили тёплое летнее солнышко. - Протяните руки к нему. Обнимите его. - Наклонитесь вперёд, назад. Потянитесь. Присели, встали. - Вам приятно и спокойно. Вы бодры и полны сил. - Откройте глаза и продолжим нашу работу.
Задача №1: Два самолёта вылетели одновременно на встречу друг другу, один со скоростью 960,4 (км/ч), другой – 1137,8 (км/ч). Через час расстояние между ними было 815 км. Определить расстояние между городами. Решение (арифметический способ): 960,4 + 1137,8 + 815 = 2913,2 (км) Ответ: 2913,2 (км). Задача №2: Катер шёл 3,7 часа по озеру со скоростью 42 (км/ч), потом вошёл в реку, впадающей в это озеро и двигался ещё 4,3 часа. Сколько километров прошёл катер, если скорость течения реки 2,7 (км/ч)? Анализ условия: Вид движения V t S По озеру 42 (км/ч) 3,7 (ч) Против течения 4,3 (ч) Скорость течения 2,7 (км/ч). Сколько всего километров прошёл катер? Решение (арифметический способ):
Ответ: весь путь займёт 324,59 (км). Задача №3 (сборник по подготовке к ГИА): Расстояние от А до Б первый автомобиль проезжает в 1,5 раза быстрее, чем второй. Найти скорости автомобилей, если скорость первого на 18 (км/ч) больше скорости второго. Решение (алгебраический способ): Пусть меньшая скорость автомобиля составляет Х (км/ч). Тогда, скорость большая составит (Х+18) (км/ч). Большая скорость в 1,5 раза больше. Составим и решим уравнение: 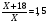 1,5Х - Х = 18 Х = 36 (км/ч) – скорость меньшая, тогда 36 + 18 = 54 (км/ч) – большая скорость. Ответ: 36 (км/ч); 54 (км/ч). |