Урок алгебры и русского языка по теме «Степенные функции, их свойства и графики». (11 класс) «Быть опровергнутым этого опасаться нечего; опасаться следует другого быть непонятым»
 Скачать 34.31 Kb. Скачать 34.31 Kb. |
| Интегрированный урок алгебры и русского языка по теме «Степенные функции, их свойства и графики». (11 класс) «Быть опровергнутым – этого опасаться нечего; опасаться следует другого – быть непонятым». И.Кант Тип урока: урок применения знаний на практике. Форма урока: урок - практикум. Цели урока:
3. Закрепление научных понятий, предусмотренных учебной программой и умелое их использование в создании текстов различных стилей речи. Задачи урока: 1. Научить оперировать имеющимся потенциалом знаний по теме «Степенные функции» в конкретной ситуации. 2. Учить практически применять функциональные стили речи на уроках математики. 3. Использовать новые информационные технологии в процессе обучения. 4. Вовлечь учащихся в активную практическую деятельность. 5. Совершенствовать навыки выступления перед аудиторией. ХОД УРОКА.
Учитель русского языка. Каждый день мы с вами говорим, обмениваемся мыслями, делимся впечатлениями, сообщаем друг другу что-либо, оказываем воздействия на чувства людей. В зависимости от цели высказывания мы используем различные стили речи. Выбранный стиль зависит также от того, где, в какой обстановке мы говорим: в официальной, неофициальной, деловой, непринужденной. Сегодня на уроке обстановка не будет однообразной. Как вы думаете знание каких функциональных стилей речи нам понадобится? - Для какого стиля характерно преобладание слов с эмоциональной экспрессивной окраской, используются общеупотребительные слова? (разговорный). - Тип речи, при помощи которого разъясняется, отрицается или подтверждается какая-либо мысль (рассуждение). - Разговор двух или более лиц (диалог). - Несколько предложений, связанных по смыслу и грамматически (текст). - Стиль речи, цель которого передача деловой информации (официально-деловой). Перед нами на сегодняшнем уроке поставлена цель: умело использовать тексты различных стилей речи при закреплении научных понятий из области математики. Учитель математики. Сегодня мы с вами должны обобщить понятие степени с действительным показателем и рассмотреть применение свойств степенных функций в конкретных ситуациях. 3. Историческая справка. «Обобщение понятия степени» (выступление ученика). Анализ прослушанного текста. Учащиеся определяют стиль, приводят доказательства. (Приложение 1). Д/з по русскому языку: написать рецензию на предложенный текст. 4. Обобщение теоретического материала по теме урока. Презентация (выполняет учащийся с применением новых информационных технологий). (Приложение 2) 5. Устные упражнения (подготовить за доской). 1) Вычислите: 2) Какое из выражений имеет смысл: 3) Найдите область определения функции: 4) Найдите наибольшее и наименьше значения функции: а) у = б) у = в) у = 5) По геометрической модели составить аналитическую: 6. Разминка. Учитель математики. Работа в тетрадях по вариантам. 1 вариант 2 вариант № 1260 (б) № 1261 (в) Решить графически уравнение: Решить графически систему уравнений:  Прочитать задание. Какие инструкции должны быть применены при выполнении данных заданий? Выполняют задание. Проверка.  х = 1 х = 1  (0;0) и (1;1) (0;0) и (1;1)Учитель русского языка. При выполнении этого задания вы использовали инструкцию. К жанру какого стиля относится инструкция? По каким признакам вы это определили? 7. Самостоятельная работа (с проверкой за доской). Теперь вы знаете, что от точного выполнения инструкций зависит правильность выполнения задания. Приступаем к самостоятельной работе. Проговорите по себя алгоритмы составления уравнения касательной к графику функции у = f(x) и вычисления площадей плоских фигур с помощью определенного интеграла. 1 вариант 2 вариант № 1278 (г) № 1283 (в) Напишите уравнение касательной к Найдите площадь фигуры, ограниченной графику функции у = в точке с абсциссой а = 2. Проверка с объяснениями. 8. Построить и прочитать график функции. № 1286. у = 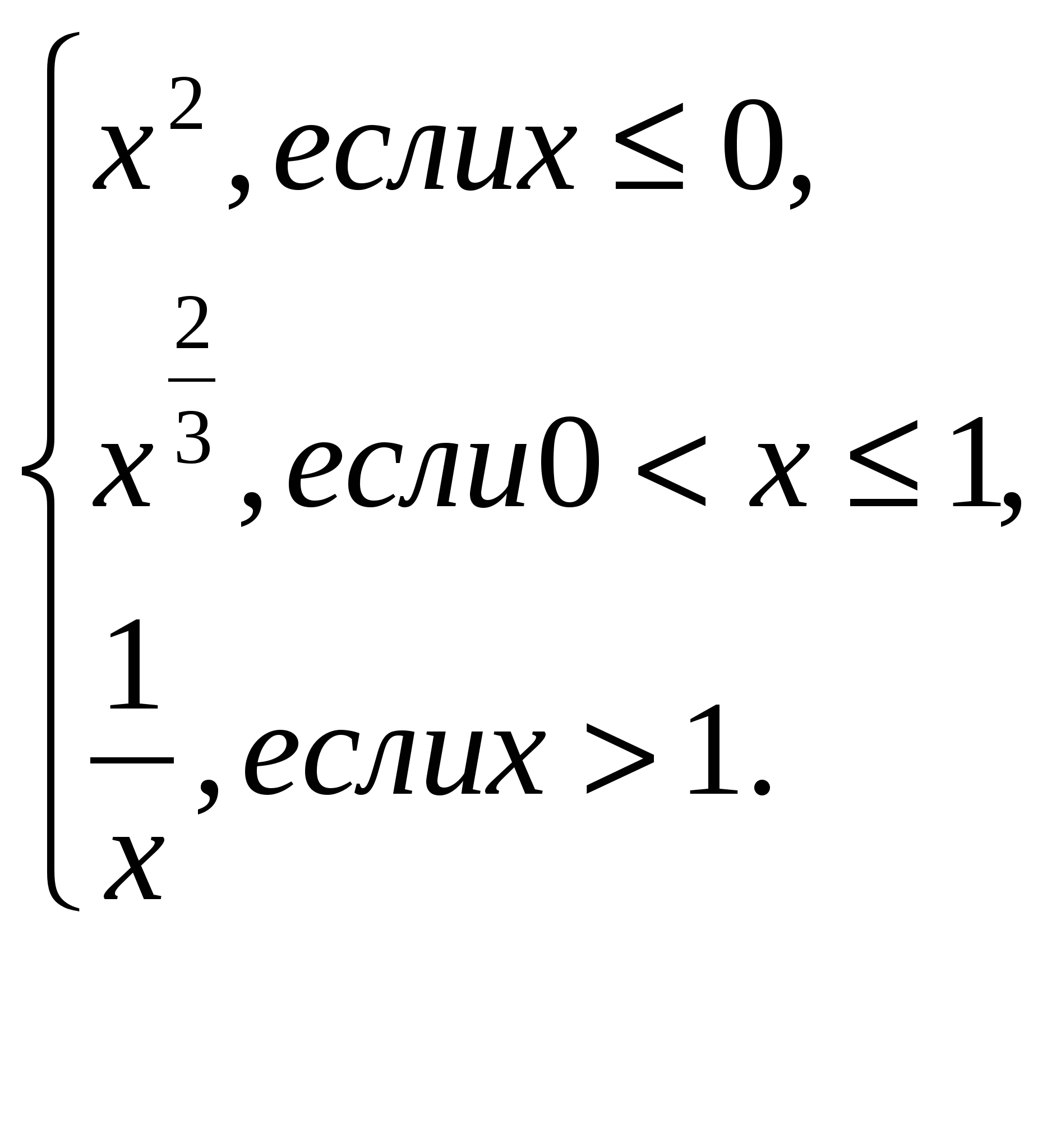 9. Итог урока. Учитель математики. Учащиеся. Учитель русского языка (с переходом на рекламу). 10. Реклама. (Приложение 3). |