|
Учебник «Геометрия 10-11»
Пояснительная записка
Рабочая программа по геометрии составлена на основе федерального образовательного стандарта 2004 года и Программы общеобразовательных учреждений Геометрия 10-11 классы, - М.Просвещение, 2009. Составитель Т. А. Бурмистрова.
Рабочая программа опирается на УМК:
- Учебник «Геометрия 10-11», М. Мросвещение 2008г. Авторы: Л. С. Атанасян и др.
- Дидактические материалы, М. Просвещение 2009, автор Б. Г. Зив
- Самостоятельные контрольные работы , М. Илекса 2003, авторы: А. П. Ершова, В. В.Голобородько.
Рабочая программа составлена на основе следующих нормативных документов:
Федеральный компонент государственного образовательного стандарта, утвержденный Приказом Минобразования РФ № 1089 от 05.03.2004;
Примерные программы, созданные на основе федерального компонента государственного образовательного стандарта, рекомендованные Министерством образования и науки РФ приказ № 03-1263 от 07.07.2005. Государственная программа для общеобразовательных школ, гимназий, лицеев. Математика. Составители: Г.М. Кузнецова, Н.Г. Миндюк. Рекомендовано Департаментом образовательных программ и стандартов общего образования Министерства образования Российской Федерации, 2002 год. Программа общеобразовательных учреждений АЛГЕБРА И НАЧАЛА АНАЛИЗА 10-11 классы. Составитель: Т.А. Бурмистрова. Москва «Просвещение», 2009 год.
Областного базисного учебного плана Челябинской области ( приказ Министерства образования и науки Челябинской области от 16.06.2011 г. № 04-997)
Приказа Министерства образования и науки России «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2013-2014 учебный год»
Учебный план МКОУ Лебедёвской СОШ на 2013 – 2014 учебный год
Общая характеристика учебного предмета
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательная линия: «Геометрия». В рамках указанной содержательной линии решаются следующие задачи:
изучение свойств пространственных тел, формирование умения применять полученные знания для решения практических задач.
Цели:
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса
Задачи :
Формирование понимания, что геометрические формы являются идеализированными образами реальных объектов;
Овладение языком геометрии в устной и письменной форме, геометрическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин;
Овладение практическими навыками использования геометрических инструментов для изображения фигур, нахождения их размеров;
Развитие логического мышления, алгоритмической культуры, пространственного воображения, интуиции, необходимых для продолжения образования и для самостоятельной деятельности;
Формирование умения проводить аргументацию своего выбора или хода решения задачи;
Формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
В программу включены все рекомендуемые темы для 11 класса. Рабочая программа рассчитана на 68 часов: 2 часа в неделю. В течение года планируется провести 3 контрольные работы и 4 зачета. В соответствии с инструктивно - методическим письмом «О преподавании математики в 2013-2014 учебном году в общеобразовательных учреждениях Челябинской области» дополнительно запланировано 3 самостоятельные работы по стержневым линиям курса геометрии 11 класса
В начале года запланированы два часа на повторение курса геометрии 10 класса и входящей контрольной работы. Они взяты из повторения, отведенного на конец года. Таким образом, заключительное повторение составляет не 14 часов, а 12.
При организации учебного процесса будет обеспечена последовательность изучения учебного материала: новые знания опираются на недавно пройденный материал; обеспечено поэтапное раскрытие тем с последующей их реализацией.
Основные типы учебных занятий:
урок изучения нового учебного материала;
урок закрепления и применения знаний;
урок обобщающего повторения и систематизации знаний;
урок контроля знаний и умений.
Основным типом урока является комбинированный.
Формы организации учебного процесса: индивидуальные, групповые, индивидуально-групповые, фронтальные.
На уроках используются такие формы занятий как:
практические занятия;
тренинг;
консультация;
лекция.
Формы контроля: текущий и итоговый. Проводится в форме контрольных работ, рассчитанных на 45 минут, и самостоятельных работ на 15 – 20 минут с дифференцированным оцениванием .
Текущий контроль проводится с целью проверки усвоения изучаемого и проверяемого программного материала; содержание определяются учителем с учетом степени сложности изучаемого материала, а также особенностей обучающихся класса. Итоговые контрольные работы проводятся:
- после изучения наиболее значимых тем программы, - в конце учебной четверти, - в конце полугодия.
Требования к уровню подготовки выпускников.
Знать/понимать:
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки, возникновения и развития геометрии;
возможности геометрического языка как средства описания свойств реальных предметов и их взаимного расположения;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
Уметь:
соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; различать и анализировать взаимное расположение фигур;
изображать геометрические фигуры и тела, выполнять чертеж по условию задачи;
решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;
проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;
вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций;
применять координатно-векторный метод для вычисления отношений, расстояний и углов;
строить сечения многогранников и изображать сечения тел вращения.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Содержание программы учебного курса.
Векторы в пространстве
Понятие вектора в пространстве. Сложение и вычитание векторов. Умножение вектора на число. Компланарные векторы.
Основная цель: закрепить известные учащимся из курса планиметрии сведения о векторах и действиях над ними, ввести понятие компланарных векторов в пространстве и рассмотреть вопрос о разложении любого вектора по трем данным некомпланарным векторам.
Метод координат в пространстве. Движения.
Координаты точки и координаты вектора. Скалярное произведение векторов. Уравнение плоскости. Движения. Преобразование подобия.
Основная цель: сформировать умение учащихся применять векторно-координатный метод к решению задач на вычисление углов между прямыми и плоскостями и расстояний между двумя точками, от точки до плоскости.
Цилиндр, конус, шар.
Понятие цилиндра. Площадь поверхности цилиндра. Понятие конуса. Площадь поверхности конуса. Усеченный конус. Сфера и шар. Уравнение сферы. Взаимное расположение сферы и плоскости. Касательная плоскость к сфере.
Взаимное расположение сферы и прямой. Сечение цилиндрической и конической поверхностей различными плоскостями.
Основная цель: дать учащимся систематические сведения об основных телах и поверхностях вращения – цилиндре, конусе, сфере, шаре.
Объемы тел
Объем прямоугольного параллелепипеда. Объемы прямой призмы и цилиндра. Объемы наклонной призмы, пирамиды и конуса. Объем шара и площадь сферы. Объемы шарового сегмента шарового слоя и шарового сектора.
Основная цель: ввести понятие объема тела и вывести формулы для вычисления объемов основных многогранников и круглых тел, изученных в курсе геометрии.
Формы и средства контроля.
Для проведения контрольных работ используется: «Программа общеобразовательных учреждений. Геометрия 10 - 11 классы, - М.Просвещение, 2009. Составитель Т. А. Бурмистрова», для проведения самостоятельных и зачетных работ - «Самостоятельные и контрольные работы по геометрии для 11 класса. Разоуровневые дидактические материалы, - М. Илекса 2003. Авторы: А. П. Ершова, В. В. Голобородько», «Поурочные разработки по геометрии 11 класс к учебному комплекту Л. С. Атанасяна. Дифференцированный подход, - М. Вако 2009. Автор В. А. Яровенко, «Дидактические материалы по геометрии 11 класс, М. Просвещение 2009. Автор Б. Г. Зив».
Тематическое планирование
№ п/п
|
НАЗВАНИЕ РАЗДЕЛА
|
Кол-во часов
|
Зачеты
|
Контрольные
работы
|
1
|
Векторы в пространстве
|
3
|
|
|
2
|
Метод координат в пространстве.
|
17
|
1
|
1
|
3
|
Цилиндр, конус и шар.
|
17
|
1
|
1
|
4
|
Объёмы тел.
|
17
|
1
|
1
|
5
|
Некоторые сведения из планиметрии
|
9
|
|
|
6
|
Обобщающее повторение. Решение задач.
|
5
|
|
|
|
Всего
|
68
|
3
|
3
|
Календарно-тематическое планирование
Геометрия 11 класс Л.С. Атанасян и др.(2 часа в неделю, всего 68 часов.)
урока
|
Глава,
§,
пункт
| Содержание |
Дата
|
Тип
урока
|
Примечания
|
|
Гл.4
|
«Векторы в пространстве» (повторение)(3ч.)
|
|
|
|
1
|
П.40-42
|
Сложение и вычитание векторов. Умножение вектора на число
|
|
Урок повторения и обобщения изученного матер.
|
|
2
|
П.43-44
|
Компланарные векторы
|
|
Урок повторения и обобщения изученного матер.
|
|
3
|
П.45
|
Разложение вектора по трем некомпланарным векторам
|
|
Урок повторения и обобщения изученного матер.
|
|
|
Гл.5
|
Метод координат в пространстве (17ч.)
|
|
|
|
|
§1
|
Координаты точки и координаты вектора (6ч.)
|
|
|
|
4
|
П46
|
Прямоугольная система координат
|
|
Урок изучения нового материала
|
|
5
|
П47
|
Координаты вектора
|
|
Урок изучения нового материала
|
|
6
|
П47
|
Координаты вектора
|
|
Комбинированный урок
|
|
7
|
П 48
|
Связь между координатами векторов и точек
|
|
Урок изучения нового материала
|
|
8
|
П49
|
Простейшие задачи в координатах
|
|
Урок изучения нового материала
|
|
9
|
П49
|
Простейшие задачи в координатах
|
|
Комбинированный урок
|
|
|
§2
|
Скалярное произведение векторов (5ч.)
|
|
|
|
10
|
П.50,51
|
Угол между векторами. Скалярное произведение векторов
|
|
Урок изучения нового материала
|
|
11
|
П.50,51
|
Угол между векторами. Скалярное произведение векторов
|
|
Комбинированный урок
|
|
12
|
П.52
|
Вычисление углов между прямыми и плоскостями
|
|
Комбинированный урок
|
|
13
|
П.52
|
Вычисление углов между прямыми и плоскостями
|
|
Комбинированный урок
|
|
14
|
П.53
|
Уравнение плоскости
|
|
Урок изучения нового материала
|
|
|
§3
|
Движения (4ч.)
|
|
|
|
15
|
П.54-57
|
Центральная, осевая, зеркальная симметрии. Параллельный перенос.
|
|
Урок изучения нового материала
|
|
16
|
П.54-57
|
Центральная, осевая, зеркальная симметрии. Параллельный перенос.
|
|
Комбинированный урок
|
|
17
|
П.58
|
Преобразование подобия
|
|
Урок изучения нового материала
|
|
18
|
|
Решение задач
|
|
Комбинированный урок
|
|
19
|
|
Контрольная работа №1
|
|
Урок контроля ЗУН учащихся.
|
|
20
|
|
Зачет № 1 по темам главы 5
|
|
Урок контроля ЗУН учащихся.
|
|
|
Гл.6
|
Цилиндр, конус, шар (17ч.)
|
|
|
|
|
§1
|
Цилиндр. (3ч.)
|
|
|
|
21
|
П.59
|
Понятие цилиндра.
|
|
Урок изучения нового материала
|
|
22
|
П.60
|
Площадь поверхности.
|
|
Комбинированный урок
|
|
23
|
|
Решение задач
|
|
Комбинированный урок
|
|
|
§2
|
Конус. (4ч.)
|
|
|
|
24
|
П.61
|
Понятие конуса.
|
|
Урок изучения нового материала
|
|
25
|
П.62
|
Площадь поверхности.
|
|
Комбинированный урок
|
|
26
|
П.63
|
Усеченный конус.
|
|
Комбинированный урок
|
|
27
|
|
Решение задач
|
|
Комбинированный урок
|
|
|
§3
|
Сфера(8ч.)
|
|
|
|
28
|
П.64
|
Сфера и шар.
|
|
Урок изучения нового материала
|
|
29
|
П.65
|
Уравнение сферы.
|
|
Комбинированный урок
|
|
30
|
П.66,67
|
Взаимное расположение сферы и плоскости. Касательная плоскость к сфере.
|
|
Урок изучения нового материала
|
|
31
|
П.67
|
Касательная плоскость к сфере.
|
|
Комбинированный урок
|
|
32
|
П.68
|
Площадь сферы.
|
|
Урок изучения нового материала
|
|
33
|
П.69
|
Взаимное расположение сферы и прямой
|
|
Урок изучения нового материала
|
|
34
|
П.70,71
|
Сфера, вписанная в цилиндрическую поверхность.
Сфера, вписанная в коническую поверхность.
|
|
Урок изучения нового материала
|
|
35
|
П.72,73
|
Сечения цилиндрической поверхности.
Сечения конической поверхности.
|
|
Урок изучения нового материала
|
|
36
|
|
Контрольная работа №2
|
|
Урок контроля ЗУН учащихся.
|
|
37
|
|
Зачет № 2 по темам главы 6
|
|
Урок контроля ЗУН учащихся.
|
|
|
Гл.7
|
Объемы тел (17ч.)
|
|
|
|
|
§1
|
Объем прямоугольного параллелепипеда (3ч.)
|
|
|
|
38
|
П.74,75
|
Понятие объема. Объем прямоугольного параллелепипеда
|
|
Урок изучения нового материала
|
|
39
|
П.75
|
Объем прямоугольного параллелепипеда
|
|
Комбинированный урок
|
|
40
|
|
Решение задач
|
|
Комбинированный урок
|
|
|
§2
|
Объем прямой призмы и цилиндра (2ч.)
|
|
|
|
41
|
П.76
|
Объем прямой призмы.
|
|
Урок изучения нового материала
|
|
42
|
П.77
|
Объем цилиндра.
|
|
Урок изучения нового материала
|
|
|
§3
|
Объем наклонной призмы, пирамиды, конуса (5ч.)
|
|
|
|
43
|
П.78
|
Вычисление объемов тел с помощью интеграла.
|
|
Урок изучения нового материала
|
|
44
|
П.79
|
Объем наклонной призмы.
|
|
Урок изучения нового материала
|
|
45
|
П.80
|
Объем пирамиды.
|
|
Урок изучения нового материала
|
|
46
|
П81
|
Объем конуса.
|
|
Урок изучения нового материала
|
|
47
|
|
Решение задач
|
|
Комбинированный урок
|
|
|
§4
|
Объем шара и площадь сферы (5ч.)
|
|
|
|
48
|
П.82
|
Объем шара
|
|
Урок изучения нового материала
|
|
49
|
П.83
|
Объем шарового сегмента, шарового слоя и шарового сектора
|
|
Урок изучения нового материала
|
|
50
|
П.83
|
Объем шарового сегмента, шарового слоя и шарового сектора
|
|
Комбинированный урок
|
|
51
|
П.84
|
Площадь сферы
|
|
Урок изучения нового материала
|
|
52
|
|
Решение задач
|
|
Комбинированный урок
|
|
53
|
|
Контрольная работа №3
|
|
Урок контроля ЗУН учащихся.
|
|
54
|
|
Зачет № 3 по темам главы 7
|
|
Урок контроля ЗУН учащихся.
|
|
|
Гл.8
|
Некоторые сведения из планиметрии (9ч.)
|
|
|
|
55
|
§1
|
Углы и отрезки, связанные с окружностью
|
|
Урок повторения и обобщения изученного матер.
|
|
56
|
§1
|
Углы и отрезки, связанные с окружностью
|
|
Урок повторения и обобщения изученного матер.
|
|
|
§2
|
Решение треугольников (4ч.)
|
|
|
|
57
|
П.90,91
|
Теорема о медиане. Теорема о биссектрисе.
|
|
Урок повторения и обобщения изученного матер.
|
|
58
|
П.92,93
|
Формулы площади треугольника.
|
|
Урок повторения и обобщения изученного матер.
|
|
59
|
П.94
|
Задача Эйлера
|
|
Урок изучения нового материала
|
|
60
|
§3
|
Теоремы Менелая
|
|
Урок изучения нового материала
|
|
61
|
§3
|
Теоремы Чевы.
|
|
Урок изучения нового материала
|
|
62
|
§3
|
Решение задач
|
|
Комбинированный урок
|
|
63
|
§4
|
Эллипс, гипербола и парабола
|
|
Урок изучения нового материала
|
|
|
|
Заключительное повторение (5ч.)
|
|
Урок повторения и обобщения изученного матер.
|
|
|
|
|
|
|
|
РЕСУРСНОЕ ОБЕСПЕЧЕНИЕ РАБОЧЕЙ ПРОГРАММЫ
Список литературы:
Федеральный компонент государственных образовательных стандартов среднего (полного) общего образования (приказ Минобрнауки от 05.03.2004г. № 1089).
Примерная программа общеобразовательных учреждений по геометрии 10–11 классы, к учебному комплексу для 10-11 классов (авторы Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др., составитель Т.А. Бурмистрова – М: «Просвещение», 2008 – М: «Просвещение», 2008. – с. 19-21).
Геометрия: учеб, для 10—11 кл. / [Л. С. Атанасян, В. Ф. Бутузов, С. В. Кадомцев и др.]. — М.: Просвещение, 2009.
Зив Б.Г. Геометрия: дидактические материалы для 11 кл. / Б.Г. Зив, В.М. Мейлер. — М.: Просвещение, 2009.
О преподавании математики в 2010/2011 учебном году. Методическое письмо. Под ред. Ященко И.В., Семенова А.В. (2010, 240с.)
Дополнительная литература:
Математика 5-11 классы: нетрадиционные формы организации контроля на уроках / авт.-сост. М.Е. Козина, О.М. Фадеева. - Волгоград, Учитель, 2007;
Конструирование современного урока математики: кн. для учителя / С.Г. Манвелов. – М.: Просвещение,2009.
Интернет-ресурс
1. www. edu - "Российское образование" Федеральный портал.
2. www. school.edu - "Российский общеобразовательный портал".
3. www.school-collection.edu.ru/ Единая коллекция цифровых образовательных ресурсов
4. www.mathvaz.ru - docье школьного учителя математики
5. www.it-n.ru "Сеть творческих учителей"
6. www .festival.1september.ru Фестиваль педагогических идей "Открытый урок»
КОНТРОЛЬНЫЕ РАБОТЫ
Контрольная работа № 1 «Метод координат в пространстве»
Вариант №1.
10. Найдите координаты вектора 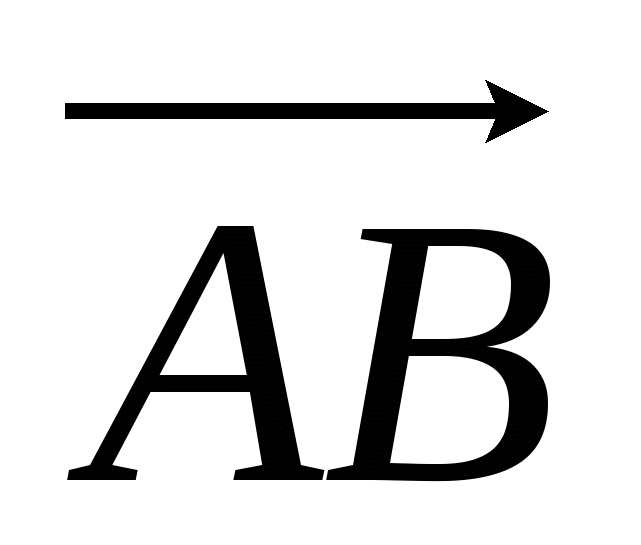 , если А(5; -1; 3), В(2; -2; 4). , если А(5; -1; 3), В(2; -2; 4).
20. Даны векторы 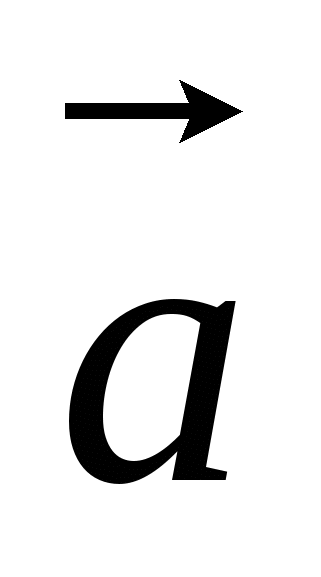 {3; 1; -2}, {3; 1; -2}, 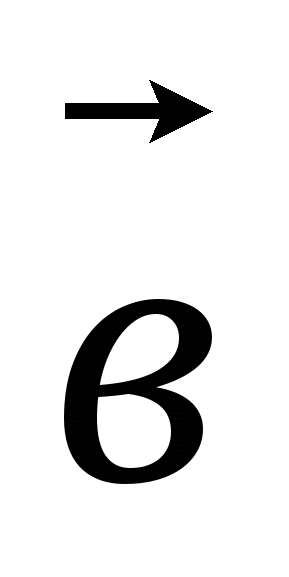 {1; 4; -3}. Найдите {1; 4; -3}. Найдите 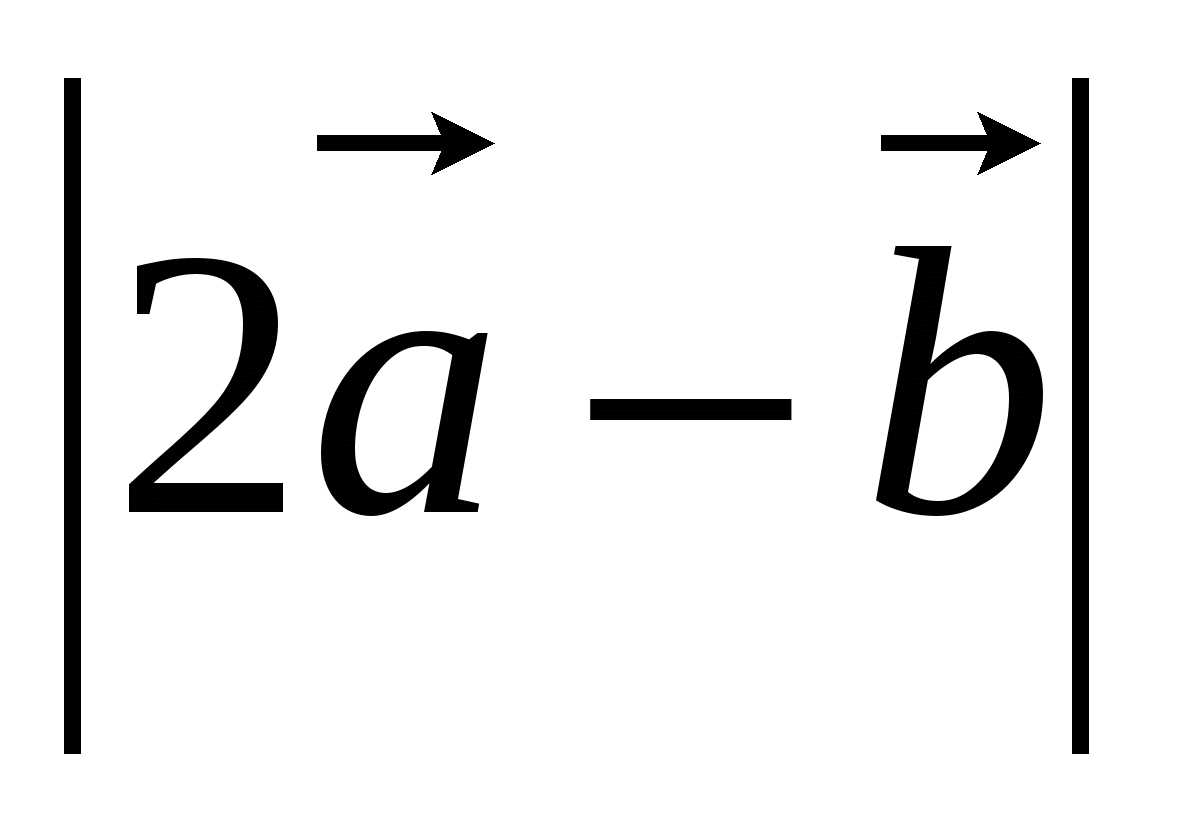 . .
3. Дан куб АВСDА1В1С1D1. Найдите угол между прямыми АD1 и ВМ, где М – середина ребра DD1.
4. Вычислите скалярное произведение векторов 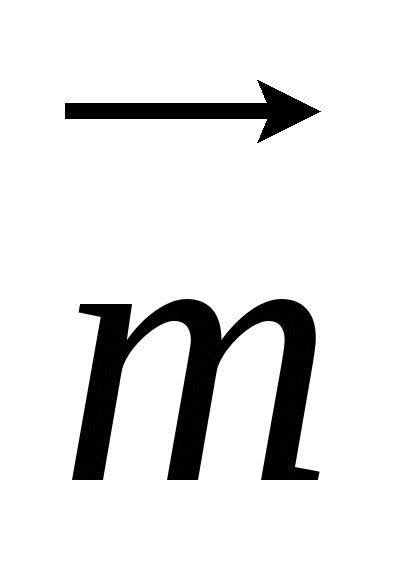 и и 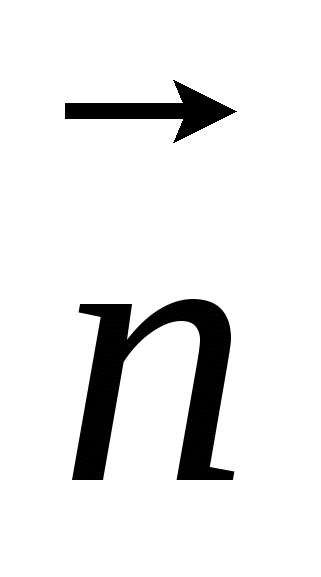 , если , если 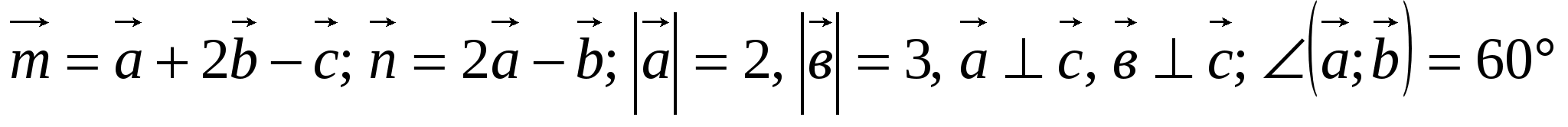 . .
Вариант №2
10. Найдите координаты вектора 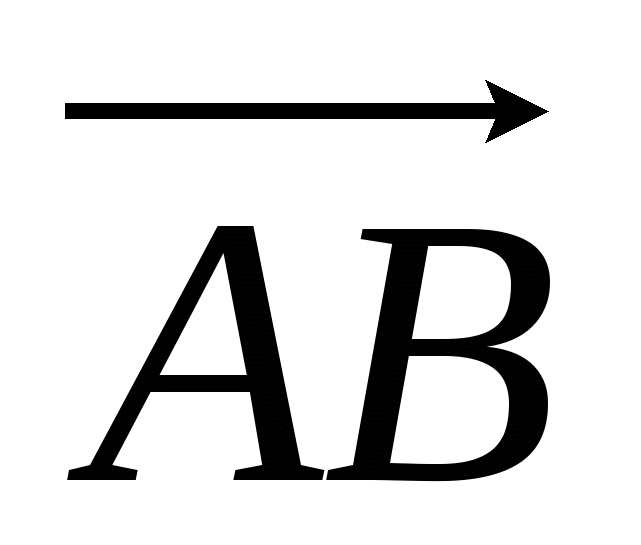 , если А(6; 3; -2), В(2; 4; -5). , если А(6; 3; -2), В(2; 4; -5).
20. Даны векторы 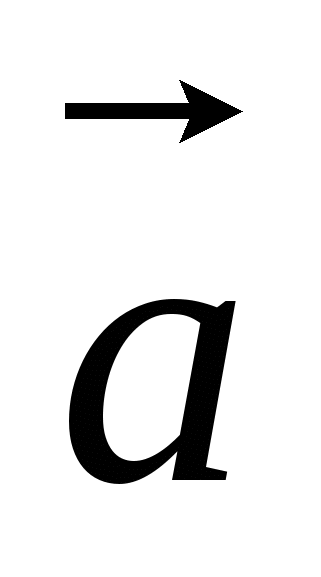 {5; -1; 2}, {5; -1; 2}, 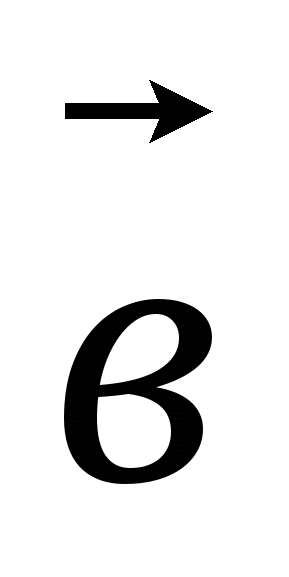 {3; 2; -4}. Найдите {3; 2; -4}. Найдите 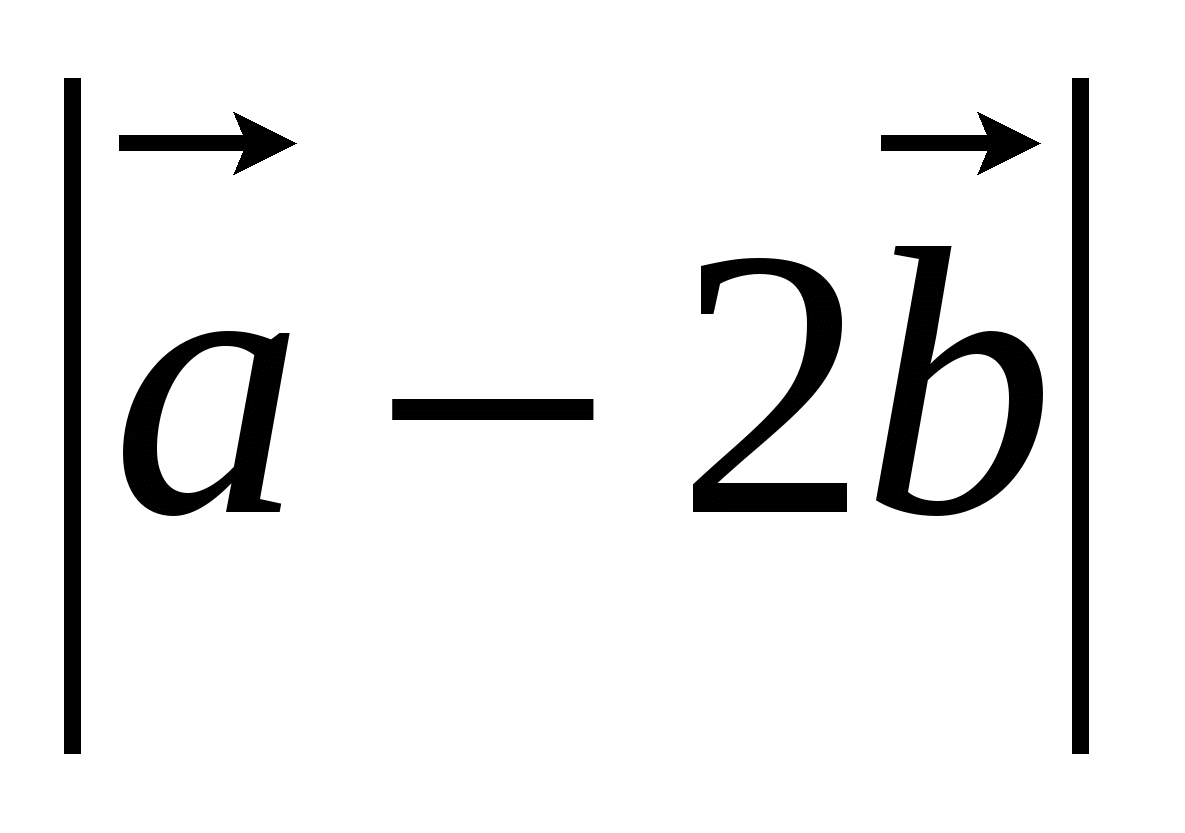 . .
3. Дан куб АВСDА1В1С1D1. Найдите угол между прямыми АС и DС1.
4. Вычислите скалярное произведение векторов 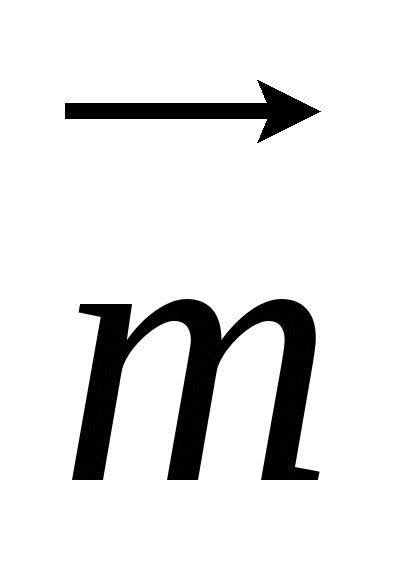 и и 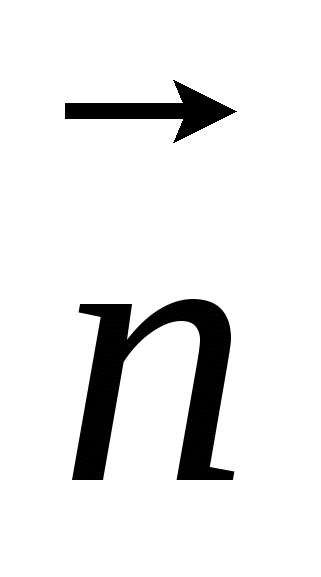 , если , если 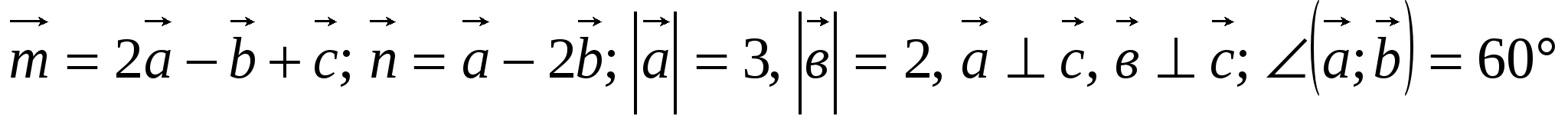 . .
Контрольная работа № «Цилиндр, конус и шар»
Вариант №1.
10. Осевое сечение цилиндра – квадрат. Площадь основания цилиндра равна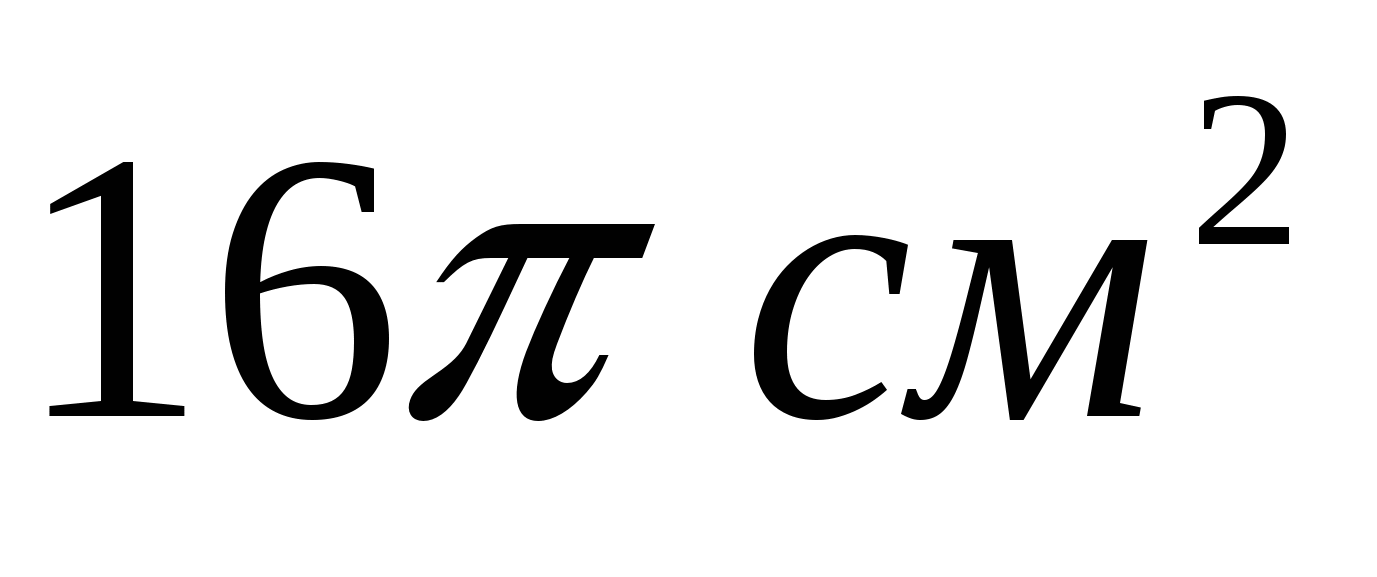 . Найдите площадь полной поверхности цилиндра. . Найдите площадь полной поверхности цилиндра.
20. Высота конуса равна 6см. Угол при вершине осевого сечения равен 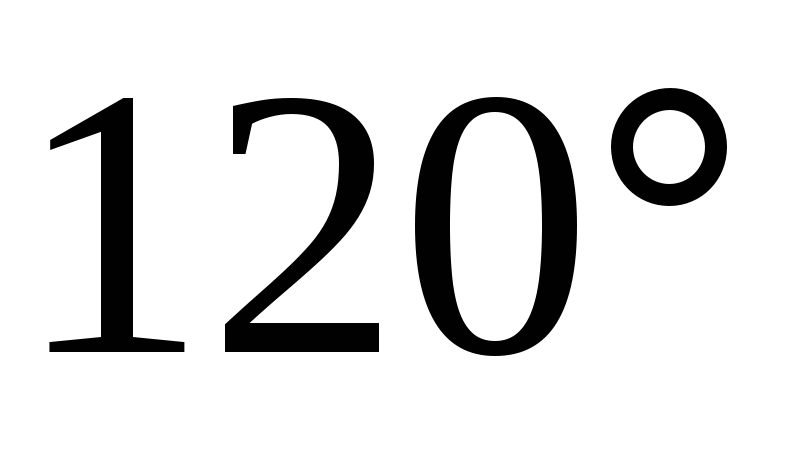 . .
а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен  . .
б) Найти площадь боковой поверхности конуса.
3. Диаметр шара равен 2р. Через конец диаметра проведена плоскость под углом 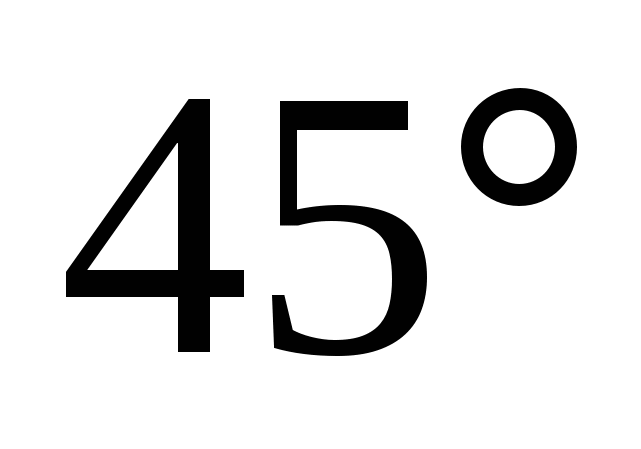 к нему. Найдите длину линии пересечения сферы этой плоскостью. к нему. Найдите длину линии пересечения сферы этой плоскостью.
Вариант №2
10. Осевое сечение цилиндра – квадрат, диагональ которого равна 4см. Найдите площадь полной поверхности цилиндра.
20. Радиус основания конуса равен 6см, а образующая наклонена к плоскости основания под углом  . .
а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен  . .
б) Найти площадь боковой поверхности конуса.
3. Диаметр шара равен 4р. Через конец диаметра проведена плоскость под углом  к нему. Найдите площадь сечения шара этой плоскостью. к нему. Найдите площадь сечения шара этой плоскостью.
Контрольная работа № 3 «Объёмы тел»
Вариант №1.
10. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол  . Найдите отношение объёмов конуса и шара. . Найдите отношение объёмов конуса и шара.
20. Объём цилиндра равен 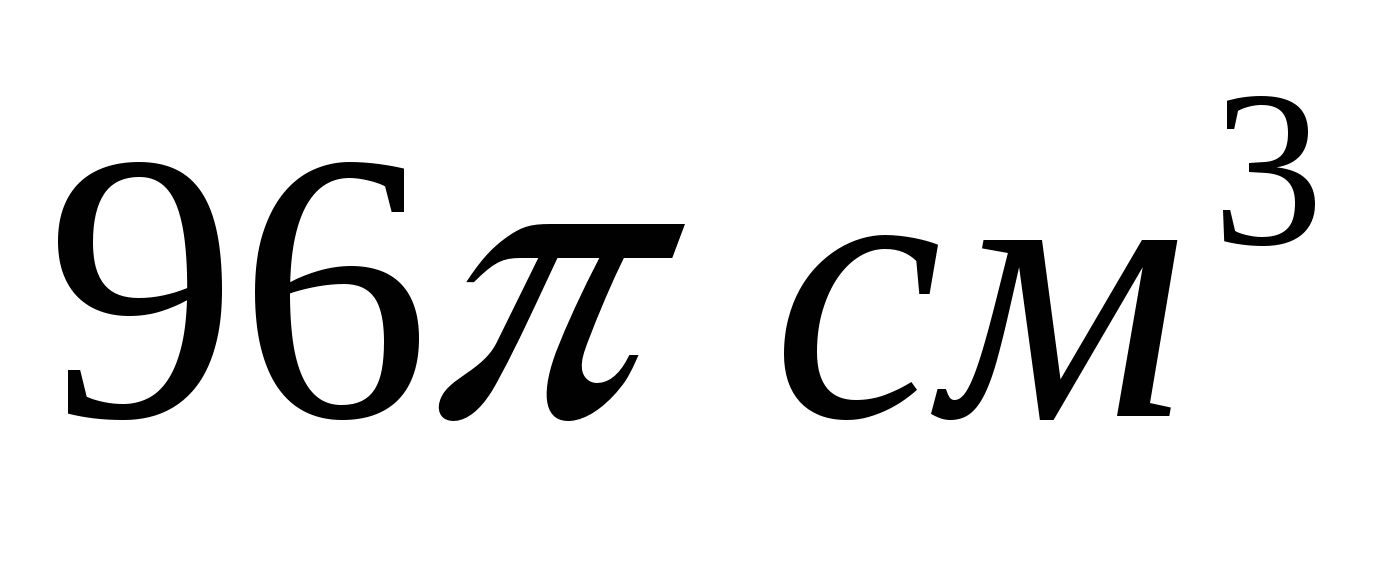 , площадь его осевого сечения , площадь его осевого сечения 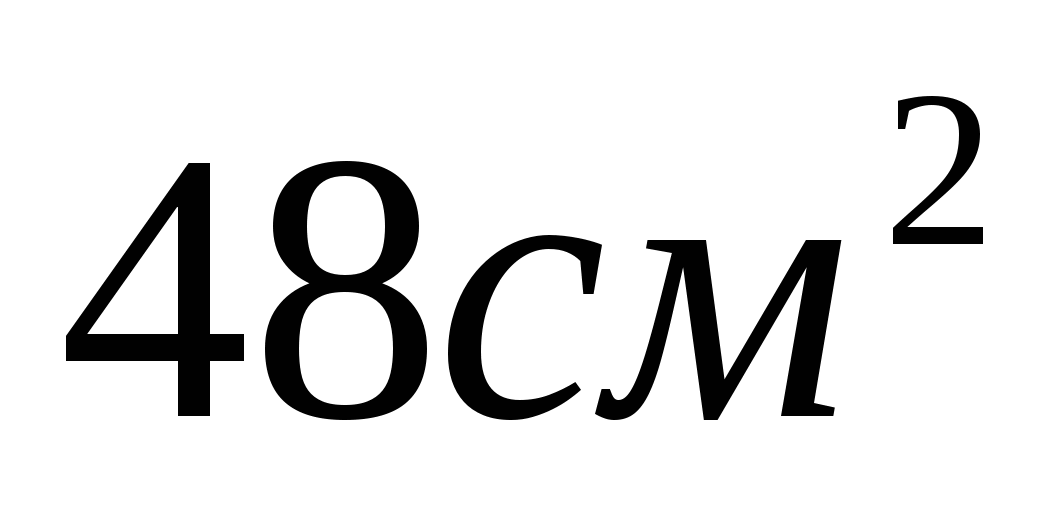 . Найдите площадь сферы, описанной около цилиндра. . Найдите площадь сферы, описанной около цилиндра.
3. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен  . Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол . Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол 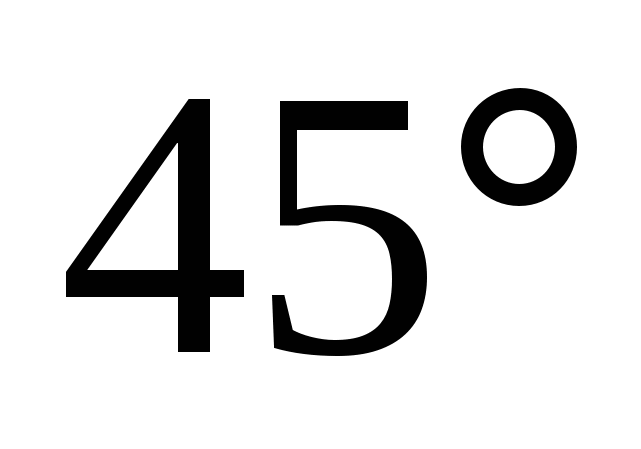 . Найдите объём конуса. . Найдите объём конуса.
Вариант №2.
10.В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
20. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объёмов шара и цилиндра.
3. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен  . Диагональ большей боковой грани призмы составляет с плоскостью её основания угол . Диагональ большей боковой грани призмы составляет с плоскостью её основания угол 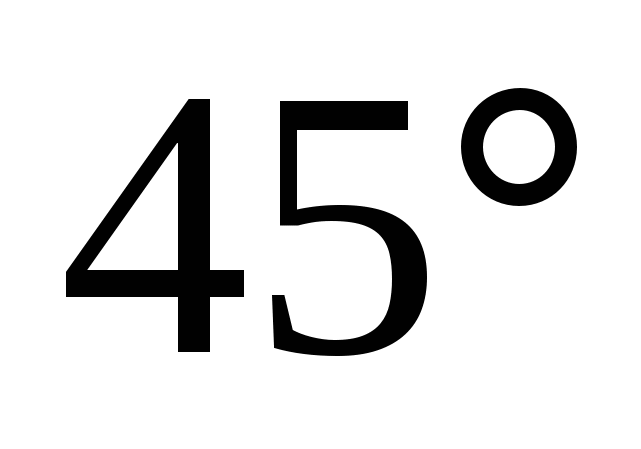 . Найдите объём цилиндра. . Найдите объём цилиндра.
В каждой контрольной работе кружочком отмечены задания, соответствующие уровню обязательной подготовки.
|
|
|
 Скачать 268.76 Kb.
Скачать 268.76 Kb.