«Степень с рациональным показателем»

Скачать 46.88 Kb. Название «Степень с рациональным показателем» Дата 05.03.2016 Размер 46.88 Kb. Тип Самостоятельная работа

Открытый урок по алгебре и началам анализа в 11 классе Тема: «Степень с рациональным показателем» Математика-это музыка разума. Музыка-это математика чувств. (Джеймс Джозеф Сильвестр) Цели урока: Обобщение и систематизация знаний, умений, навыков. Актуализация опорных знаний в условиях сдачи ЕГЭ. Контроль и самоконтроль знаний, умений, навыков с помощью тестов. Развитие умения сравнивать, обобщать. План урока. Формулировка цели урока Устная работа «Дополните предложение», «Верю – не верю!» Решение серии примеров на основе демонстрационного варианта ЕГЭ Решение примера на упрощение выражения (из ЕГЭ) с обсуждением наиболее “тонких” мест Физминутка. Самостоятельная работа на основе демонстрационного варианта ЕГЭ Задание на дом (на листочках) Подведение итогов урока. Оборудование: проектор. 1. Друзья! Перед вашими глазами часть высказывания английского математика Джеймса Джозефа Сильвестра (1814–1897) о математике “Математика – это музыка разума”. Не правда ли, как романтично? Вопрос. А как вы думаете, как определил он музыку? “Музыка – это математика чувств”. К чувствам мы можем отнести различного рода переживания. В этом году одной из причин ваших и моих переживаний является успешная сдача ЕГЭ и, как следствие, поступление в ВУЗ. Очень хочется, чтобы преобладали положительные эмоции. Должна быть уверенность, а это наши знания и навыки. Сегодня на уроке мы продолжим подготовку к ЕГЭ, повторяя и обобщая понятие степени. Итак, тема сегодняшнего урока –«Степень с рациональным показателем». 2. Устная работа Дополните предложения: Степень с целочисленным показателем это - :произведение n одинаковых множителей При умножении степеней с одинаковыми основаниями:показатели складываются При делении степеней с одинаковыми основаниями :показатели вычитаются Степень степени равна:произведению показателей Степень числа а, не равного нулю с нулевым показателем равна :1 Степень произведения равна :произведению степеней Степень дроби равна :дроби степеней Степень с дробным показателем m\n есть: Степень с любым показателем p\q есть: «Верю – не верю!» 1. Имеют смысл выражения: а) б) в) с)  д)  2.  (да) 3. Уравнение имеет три корня  (нет, корень один: 7, т.к.) 3.Решение серии примеров на основе демонстрационного варианта ЕГЭ Задания выполняются самостоятельно, с последующей проверкой ответов на доске. Решение примера (из ЕГЭ). При каком целом положительном x значение выражения 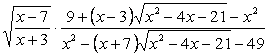ближе всего к 0,7 Решение. Вопрос. При каких значениях х данное выражение имеет смысл? Так как х – целое положительное число, то  N,  при . Проверим, не обращается ли в 0 знаменатель при х = 7.  при х = 7. Следовательно, x > 7. Преобразуем выражение: Пусть . При   положительна и возрастает  убывает  возрастает  возрастает Найдём, при каких значениях х 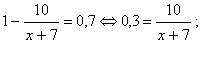 Так как f(x) –возрастающая функция, то . Найдём, какое из этих значений ближе лежит к 0,7, для чего сравним  и  Так как , то значение f(26) лежит ближе к 0,7. 5.Физминутка. 6.Самостоятельная работа на основе демонстрационного варианта ЕГЭ с последующей проверкой на доске. А теперь самое время потренироваться: перед вами примеры из демонстрационного варианта, гр.А 2009 года. Вы их видите как на доске, так и на листочках. Ваша задача – быстро решить и заполнить таблицы с ответами. Соответствие букв и чисел перед вами. Правильно вычислив или упростив выражения в таблице, вы прочтёте то, что необходимо вам при сдаче ЕГЭ. Приложение 1. 1 вариант – удача, знания, 2 вариант – уверенность. 7.Задание на дом (на листочках) №438(а,б), №439. . При каком целом положительном х значение выражения 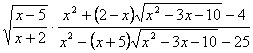 ближе всего к (–0,7) ? 8.Подведение итогов урока. Итак, сегодня на уроке мы увидели насколько широко понятие степени используется при сдаче ЕГЭ. Закрепить полученные навыки вы сможете, выполнив домашнюю работу.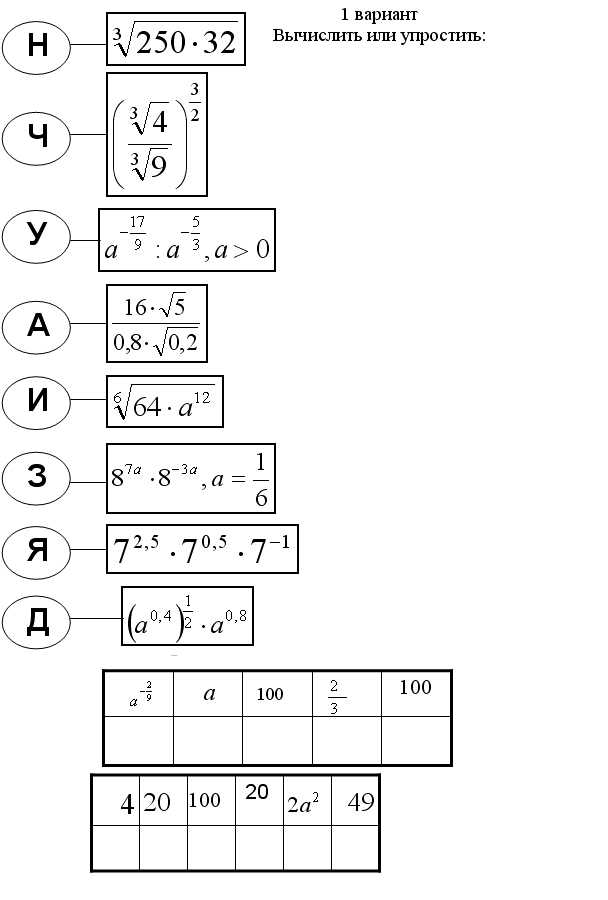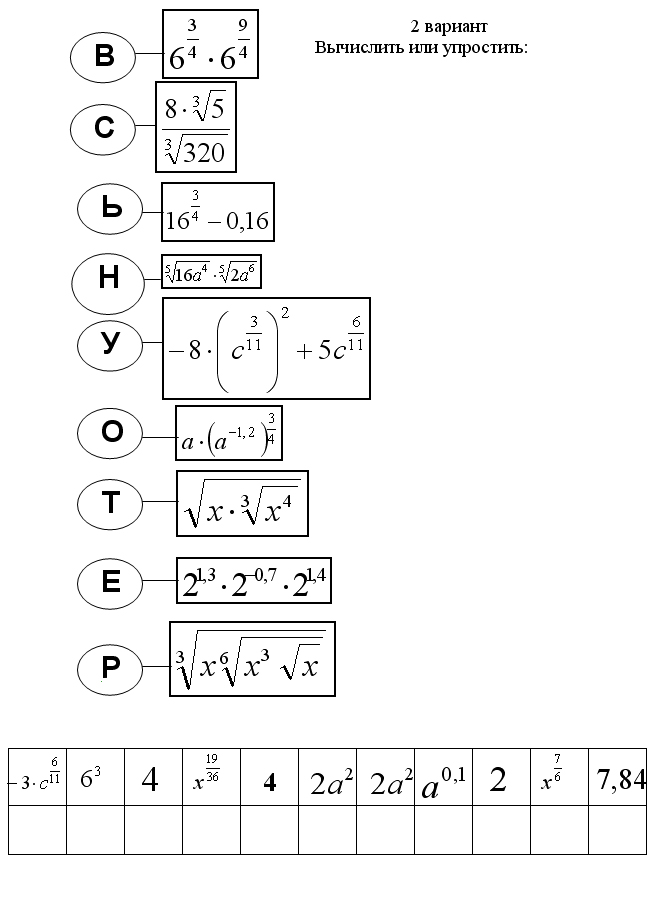