Сравнения по модулю
 Скачать 131.9 Kb. Скачать 131.9 Kb.
|
| И.А. Лаздин, С.В. Суркин СРАВНЕНИЯ ПО МОДУЛЮ Научный руководитель: С.В. Суркин Муниципальное бюджетное учреждение средняя общеобразовательная школа с углубленным изучением отдельных предметов № 16 имени Н.Ф. Семизорова sergey-vsur@yandex.ru Два целых числа, разность которых кратна данному натуральному числу Определение сравнения было сформулировано в книге К. Ф. Гаусса «Арифметические исследования». Эту работу, написанную на латинском языке, начали печатать в 1797 г., но книга вышла в свет лишь в 1801 г. из-за того, что процесс книгопечатания в то время был чрезвычайно трудоемким и длительным. Первый раздел книги Гаусса так и называется: «О сравнении чисел вообще». Сравнениями очень удобно пользоваться в тех случаях, когда достаточно знать в каких-либо исследованиях числа с точностью до кратных некоторого числа. Например, если нас интересует, на какую цифру оканчивается куб целого числа Основная цель работы: исследовать сравнения по модулю и методы их решения. Данная тема представляет определённый интерес, т.к. известно, что сравнения играют важную роль в теории чисел и алгебре. Определение сравнений. Определение. Если а и b — два целых числа и их разность а — b делится на натуральное число m, то говорят, что a и b сравнимы по модулю m. Мы выражаем это записью a ≡ b (mod m), (1) которая читается так: а сравнимо с b по модулю m. Делитель m мы предполагаем натуральным; он называется модулем сравнения. Наше высказывание (1) означает, что a — b = mk, где k — целое число. (2) Пример 1. 1) 23 ≡ 8 (mod 5), так как 23 — 8 = 15 = 5 ∙ 3; 2) 47 ≡ 11 (mod 9), так как 47–11 = 36 = 9 ∙ 4; 3) —11 ≡ 5 (mod 8), так как — 11 — 5 = —16 = 8 ∙ (-2); 4) 81 ≡ 0 (mod 27), так как 81 — 0 = 81 = 27 ∙ 3. Последний пример показывает, что вообще, вместо того, чтобы говорить: число а делится на число m, мы можем записать a ≡ 0 (mod m), так как это означает, что а — 0 = а = mk, где k — некоторое целое число. Например, вместо того, чтобы сказать, что а — четное число, мы можем записать a ≡ 0 (mod 2). Таким же образом видно, что нечетное число является числом, удовлетворяющим сравнению а ≡ 1 (mod 2). Обобщим свойства сравнений:
a1+…+ak ≡ b1+…bk(mod m)
a ≡ b (mod НОК(m1,…,mk))
Нахождение обратного элементаЗадача нахождения обратного элемента: найти b=a-1 (mod n), где a и n заданы, b неизвестно. Элемент b называется обратным к a по модулю n, если a∙b≡1(mod n). Тогда пишут, что b ≡ a–1 (mod n). Справедлива Теорема обратимости: Существует a-1 (mod n) 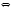 (a, n) = 1. (a, n) = 1.То есть, обратный элемент для числа существует тогда и только тогда, когда это число взаимно простое с модулем. Найти обратный элемент можно с помощью расширенного алгоритма Евклида: Пусть a > n; a, n Расширенный алгоритм Евклида находит числа x, y: ax+ny = НОД(a, n). Вычисляет цепочка равенств: a = nq1 + r1; n = r1q2 + r2; r1 = r2q3 + r3; ….. rk−2 = rk-1qk + rk; rk−1 = rkqk+1. Используя эту цепочку, восстанавливаем: rk = rk-2 – rk-1qk= rk-2 – (rk-3 – rk-2qk-1)qk = … =ax+ny. Получаем сравнение ax+ny≡1(mod n). Поскольку ny≡0(mod n), то ax≡1(mod n), а значит полученное с помощью расширенного алгоритма Евклида число x как раз и есть искомый обратный элемент к числу a по модулю n. Пример 2. Вычислить элемент, обратный а по mod n, если a=9; n=29; Решение: Воспользуемся расширенным алгоритмом Евклида: 29=9∙3+2 9=2∙4+1 2=1∙2+0 Обратный ход: 1=9-2∙4=9∙1-(29-9∙3)∙4=9∙13-29∙4. Проверка: 13∙9=117. 117≡1(mod( 29)). Ответ: обратный элемент = 13. Сравнения первой степениСравнения первой степени имеют вид 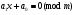 (6). Перенеся свободный член в правую часть сравнения, и меняя обозначения коэффициентов, получим (6). Перенеся свободный член в правую часть сравнения, и меняя обозначения коэффициентов, получим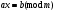 . (7) . (7)При решении таких сравнений рассматривают два случая: 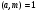 и и 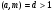 . .Теорема 1. Если 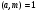 , то сравнение (7) имеет единственное решение. , то сравнение (7) имеет единственное решение.Теорема 2. Если 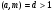 и число и число 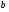 не делится на не делится на 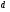 , то сравнение , то сравнение 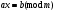 не имеет решений. не имеет решений.Теорема 3. Если 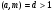 и и 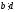 , то сравнение (7) имеет , то сравнение (7) имеет 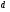 решений. решений.Решение сравнений первой степениРассмотрим 2 способа решения сравнений первой степени, в основе которых лежит приведение сравнения первой степени к равносильному сравнению с коэффициентом при 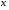 , равному единице. , равному единице.Проиллюстрируем решение сравнения этими способами на следующем примере: Решить сравнение 25х≡15(mod 17)
Практическое применение сравненийЗадача 1. Решить сравнение 6x ≡ 5 (mod 35).
Задача 2. Решить сравнение 18x = 6 (mod 24).
Задача 3. Найти остаток от деления 11210 на 5. Решение: Найти ответ на вопрос задачи, это еще и указать целое число (от 0 до 4), которое сравнимо с 112 по модулю 5. Как известно, 112  2(mod 5). Тогда по свойству 7 имеем, что 2(mod 5). Тогда по свойству 7 имеем, что 11210  210(mod 5). 210(mod 5).Очевидно, что 210 = 1024. Поскольку 1024  4(mod 5), то 11210 4(mod 5), то 11210  4(mod 5). 4(mod 5).Ответ: 4. Приведем сокращенную запись решения. 112  2(mod 5) 2(mod 5)  по свойству 7 11210  210(mod 5) 210(mod 5)  1024(mod 5) 1024(mod 5)  4(mod 5). 4(mod 5).Ответ: 4. Задача 4. Найти остаток от деления 1025 + 3117 на 10. Решение: Теперь уже будем записывать решение в краткой форме. 102  2(mod 10) 2(mod 10)  по свойству 7 1025 по свойству 7 1025  25(mod 10) 25(mod 10)  32(mod 10) 32(mod 10)  2(mod 10). 2(mod 10).311  1(mod 10) 1(mod 10)  по свойству 7 3117 по свойству 7 3117  17(mod 10) 17(mod 10)  1(mod 10). 1(mod 10).По свойству 3 1025  2(mod 10) 2(mod 10)3117  1(mod 10) 1(mod 10)_______________ 1025 + 3117  2 + 1(mod 10) 2 + 1(mod 10)  3(mod 10) 3(mod 10)Ответ: 3. Задача 5. Доказать, что при любом натуральном n число 37n+2 + 16n+1 + 23n делится нацело на 7. Решение: 37  2(mod 7), так как 37 = 5∙7 + 2. 2(mod 7), так как 37 = 5∙7 + 2.16  2(mod 7), так как 16 = 2∙7 + 2. 2(mod 7), так как 16 = 2∙7 + 2.23  2(mod 7), так как 23 = 3∙7 + 2. 2(mod 7), так как 23 = 3∙7 + 2.Тогда по свойству 7 37n+2  2n+2 (mod 7). 2n+2 (mod 7).16n+1  2n+1 (mod 7). 2n+1 (mod 7).23n  2n (mod 7). 2n (mod 7). По свойству 3, 37n+2 + 16n+1 + 23n  2n+2 + 2n+1 + 2n (mod 7). 2n+2 + 2n+1 + 2n (mod 7).Однако, 2n+2 + 2n+1 + 2n = 2n(22 + 2 + 1) = 7∙2n Это значит, 37n+2 + 16n+1 + 23n  7∙ 2n (mod 7). Но число 7∙2n делится на 7 нацело, значит, его остаток при делении на 7 равен 0. Следовательно, 7∙2n(mod 7) 7∙ 2n (mod 7). Но число 7∙2n делится на 7 нацело, значит, его остаток при делении на 7 равен 0. Следовательно, 7∙2n(mod 7)  0 0  37n+2 + 16n+1 + 23n. Это значит, что 37n+2 + 16n+1 + 23n делится на 7 нацело. Нужное утверждение доказано. 37n+2 + 16n+1 + 23n. Это значит, что 37n+2 + 16n+1 + 23n делится на 7 нацело. Нужное утверждение доказано.Задача 6. При каких натуральных n 8n+3 делится нацело на 13. Решение: Для ответа на поставленный вопрос необходимо решить сравнение 8n+3≡0 (mod 13). Находим НОД(8,13)=1, значит сравнение имеет единственное решение: 8n+3 ≡ 0 (mod 13) 8n ≡ - 3 (mod 13) 8n ≡ -3 +13 (mod 13) 8n≡10 (mod 13) 4n≡5 (mod 13) 4n≡5+13 (mod 13) 4n≡18 (mod 13) 2n≡9 (mod 13) 2n≡22 (mod 13) n≡11 (mod 13) Значит 8n+3 делится на 13, тогда и только тогда, когда n =13k+11 Задача 7. Найдите все пары чисел х и у, удовлетворяющих уравнению 7х-23у=131. Решение: Поскольку 23≡2 (mod 7), получаем сравнение 2у≡ -131(mod 7) или 2у≡ 9≡2(mod 7), т.е y≡1(mod 7). Итак, у=7k+1, подставляя это выражение в изначальное уравнение, получаем: 7х+23(7k+1) = 131 7х=154+23∙7k х = 22+23k Ответ: (22+23k; 7k+1) |
 a ≡ c (mod m)
a ≡ c (mod m) Z)
Z)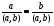 (mod m)
(mod m)