Решим уравнение. Преобразуем знаменатели в произведение
 Скачать 109.67 Kb.
|
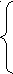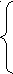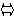| №1 Решим уравнение  .Преобразуем знаменатели в произведение:  .Наименьший общий знаменатель (НОЗ) - х(х-2)(х+2). Получим уравнение:  .Уравнение равносильно системе:  2х+(х-2)(х-4) –(х+2)=0, 2х +х2-6х +8 –х - 2 =0, х ≠ 0, х ≠ 0,х-2 ≠ 0, х ≠ 2, х+2 ≠ 0. х ≠ -2. Решим квадратное уравнение: х2 - 5х +6 = 0, х1 = 2, х2 = 3. Так как х ≠ 2, то 2 – посторонний корень. Ответ: х =3 . №2 Решим уравнение | х - 5 | + | 2х + 5 | = 3х. Левая часть уравнения положительна, значит 3х >0, х > 0. Если х > 0, то 2х +5 >0. Используя определение модуля, получим уравнение: | х - 5 | + 2х + 5 = 3х. 1. При х-5 ≥ 0 х - 5 + 2х + 5 = 3х. После преобразований уравнения получится верное числовое равенство: 0 = 0. Это означает, что решением уравнения являются все числа, удовлетворяющие условию х-5 ≥ 0, х≥5. 2. При х-5 <0 -х + 5 + 2х + 5 = 3х, -2х = -10, х = 5, что не удовлетворяет условию х-5 <0. Ответ: х ≥ 5 № 3 Решим уравнение (х2 + 3х – 4 )3 + ( 2х2 -5х + 3 )3 = (3х2 – 2х -1 )3. Разложим квадратные трёхчлены: х2 + 3х – 4, 2х2 -5х + 3 и 3х2 – 2х -1 на множители, используя формулу ах2 +bx +c = a( x- x1)(x- x2). х2 + 3х – 4= (х-1)(х+4), 2х2 -5х + 3 = 2(х-  )(х-1), 3х2 – 2х -1 = 3(х+ )(х-1). Получим уравнение (х-1)3(х+4)3 + (2х -3)3(х-1)3 = (3х +1)3(х-1)3, (х-1)3(х+4)3 + (2х -3)3(х-1)3 − (3х +1)3(х-1)3=0, (х-1)3( (х+4)3 + (2х -3)3 − (3х +1)3 ) = 0, 1. (х-1)3 =0, х-1 = 0, х =1. 2. (х+4)3 + (2х -3)3 − (3х +1)3 = 0, ( (х+4)3 + (2х -3)3) − (3х +1)3 =  0,Применим в скобках сумму кубов: ( 3х +1) ( ( х+4)2 − (х+4)(2х+3) + (2х−3)2−(3х+1)3) = 0, ( 3х +1) ( (3х2 − 9х + 37) −( 3х +1)2) =0, 3х +1 =0, х = − . (3х2 − 9х + 37) −( 3х +1)2 = 0.(*)После преобразований уравнения (*) получим: 2х2 + 5х− 12 = 0, х1=−4, х2 = .Ответ: х=−4, х = − , х =1, х = .№4 Решим уравнение  .3х2 −2х +8 >0 при всех действительных значениях х, а значит, и 3х2 −2х +15>0. ОДЗ: все действительные числа. Пусть 3х2 −2х +8 = t, t > 0. Получим уравнение  , (*)Возведём обе части уравнения (*) в квадрат: t + 7 + 2  , =21−t. (**)Это уравнение будет иметь корни при условии 21−t≥ 0, t ≤ 21. Возведём обе части уравнения (**) в квадрат: t(t+7) = 441 − 42t + t2, 49t − 441 = 0, t = 9, 9 удовлетворяет условию 0< t ≤ 21. Вернёмся к переменной х: 3х2 −2х +8 =9, 3х2 −2х−1 =0, х1=1, х2 = − .Ответ: х = − , х=1. №5 Решим уравнение  = 6− .Решим уравнение с применением функционального метода. Пусть f(x) = , z(x) = 6 - .Левая часть уравнения - функция f(x) непрерывна и возрастающая, правая часть уравнения- функция z(x) непрерывна и убывающая. Значит, графики этих функций пересекаются в единственной точке. Абсцисса этой точки - корень исходного уравнения. Находим подбором. х = − 2 Ответ: х = − 2 №6 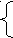 х2 − 5ху + 4у2=0, Решим систему уравнений 2х2 −у2 = 31. Первое уравнение системы решим как квадратное относительно х: х2 − 5ху + 4у2=0, а = 1, b = -5y, c = 4y2, D = 25y2 − 16y2 =9y2, x1,2 =  , x1,2 = .Если у≥0, то x1,2  , х1 =4у, х2 = у. (*)Подставим эти значения вместо х во второе уравнение системы, получим:
32у2− у2 =31, у2 =1, у1,2 = ±1, −1 не удовлетворяет условию у≥0. Подставим в (*) вместо у единицу. Получим х1 =4, х2 =1. (4; 1), (1;1) - решения системы.
2у2 −у2 =31, у2 =31, у =  . − не удовлетворяет условию у≥0.Подставим в (*) вместо у его значение , получим х1 =4, х2 =.(4 ;) , (;) – решения системы.Если у<0 , то x1,2 и:а) у1 = −1. Из (*) получим х1 = −4, х2 = −1. (−4; −1), (−1; −1) – решения системы. в) у2 = − . Из (*) получим х1 = −4, х2 = −,(−4 ;−) , (−;−) – решения системы.Ответ: (−4 ;−) , (−;−), (1;1), (4; 1), (;),(4;).№7  Решим систему уравнений (х+1)(у+1) =10, (ху+1)(х+у) =25. Преобразуем первое уравнение: (х+1)(у+1) =10, ху+х+у+1=10, (ху+1)+(х+у)=10. Введём новые переменные : ху+1 =а, х+у =с. Получим систему а+с =10, ас=25, откуда а=5 и с=5. Вернёмся к переменным х и у: ху+1=5, х+у =5, Выразим из второго уравнения х: х= 5−у. (*) Подставим это значение в первое уравнение вместо х, получим у(5−у) +1 =5, у2 −5х +4 =0, у1 =1, у2 =4. Из уравнения (*) найдём х: х1 =4, х2 =1. Решение исходной системы : (4 ; 1) , (1; 4). Ответ: (4 ; 1) , (1; 4). №8 Решим систему уравнений х2 +3ху2= 158, 3х2у +у2 = −185. Преобразуем уравнения системы: Сложим первое и второе уравнения системы, а затем вычтем из первого уравнения второе и применим для каждого получившегося уравнения соответственно сумму и разность кубов. Эти преобразования приводят к равносильной системе. Получим (х+у)3 =−27, ( х+у)3 =−33, х + у = −3,(х−у)3 = 343; ( х −у)3 = 73; х −у =7; 2х =4, х=2. Найдём у: у = −3 − х, у = − 5. Ответ: (− 5; 2). №9 Р ешим систему уравненийх +у +z =13, x2 +y2 +z2 = 91, y2 = xz. 1.Обе части первого уравнения возведём в квадрат: х2+у2+z2 +2xy + 2xz + 2yz =169, Сгруппируем слагаемые: (х2+у2+z2) +2( xy + xz + yz ) =169, вместо х2+у2+z2 подставим 91, получим 2(xy + xz + yz) =78, xy + xz + yz =39. Вместо xz подставим у2, xy + у2 + yz =39, у(х+у+z) =39, y∙13 =39, y=3. Подставим в исходную систему 3 вместо у:  x+z =10, x=1, z=9 или z=1, x=9.xz =9 Проверка показала, что тройки (1; 3; 9) и (9; 3; 1) чисел удовлетворяют всем уравнениям исходной системы. Ответ: (1; 3; 9), (9; 3; 1). №10 Решим неравенство x >  .х − > 0,  > 0,После преобразований в числителе, получим  > 0.Разложим числитель и знаменатель на множители: 1.х2+4х +3 = (х+1)(х+3). 2. х3 + 3х −4 =0, х=1 –корень этого уравнения, значит х3 + 3х −4 делится на х−1, (х3 + 3х −4) : (х−1) =х2 +4х+4 х3 + 3х −4 = (х2 +4х+4) (х−1) =(х+2)2 (х−1). Получим неравенство  >0, Воспользуемся методом интервалов:  − + + − + -3 -2 - 1 1 Ответ: (-3; -2)  ( -2; -1) (1; +∞).№11 Решим неравенство (х2 + 3х+1)( х2 + 3х−3) ≥ 5. Введём новую переменную: пусть х2 + 3х−3 = t, тогда х2 + 3х+1 = t+4. Получим неравенство t (t+4) ≥ 5, t2 + 4t − 5 ≥ 0, (t+5)(t−1) ≥ 0, Воспользуемся методом интервалов: + − +  −5 1 Получим t ≤ −5, t ≥ 1. Вернёмся к переменной х: 1. х2 + 3х−3 ≤ −5 2. х2 + 3х−3 ≥ 1, х2 + 3х+2 ≤ 0, х2 + 3х−4 ≥ 0, (х+2)(х+1) ≤ 0, (х−1)(х+4) ≥ 0, + − + + − +    −2 −1 −4 1 Решение неравенства 1:[−2; −1]. Решение неравенства 2: (− ∞; −4] [1;+ ∞).Объединим решения неравенств 1 и 2 – это решение исходного неравенства (− ∞; −4], [ −2; −1], [1;+ ∞). Ответ: (− ∞; −4], [ −2; −1], [1;+ ∞). №12 Решим неравенство |х2−2х −3| < |х2−х +4| . х2−х +4 > 0 при всех действительных значениях х, т.к. D <0 и а >0. Значит, |х2−х +4| = х2−х +4. Получим неравенство |х2−2х −3| < х2−х +4. Определим знаки функции f(x) = х2−2х −3 на числовой прямой: х2−2х −3 =0, (x+1)(x−3) =0. Воспользуемся методом интервалов: + − + -1 3 Итак: f(x) >0 на (− ∞; −1) (3;+ ∞);f(x) <0 на ( −1; 3). Рассмотрим два случая: 1  . х < −1, х > 3, х2−2х −3 < х2−х +4; х < −1, х > 3,х2−2х −3 − х2+х− 4 <0; х < −1, х > 3, х >7; Решение системы 1: (7;+ ∞). 2 . −1< x <3,−х2 + 2х +3 < х2−х +4; 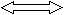−1< x <3, −1< x <3, −2х2 +3х −1 < 0 (2х−1)(х−1) > 0; В оспользуемся методом интервалов: + − +  1 Решение неравенства (2х−1)(х−1) > 0 : (− ∞; ) (1;+ ∞),Решение системы 2 : (−1; ) , (1; 3).Объединим решения систем 1 и 2: (−1; ) , (1; 3), (7;+ ∞). Ответ: (−1; ) , (1; 3), (7;+ ∞). №13 Решим неравенство  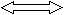< . 2х+1≥ 0, х ≥ -,ОДЗ: 2-х ≠ 0; x ≠ 2. ОДЗ: [− ;2), (2 ; + ∞).Из условия следует, что левая и правые части неотрицательны, значит, можем возвести в квадрат обе части неравенства:  .Т.к. 4 (2−х)2 > 0, то (2х+1) (2−х)2 − 4(х+1)2 < 0, Преобразуем левую часть неравенства: 2х3 − 11х2 −4х <0, х( 2х2− 11х −4 ) <0.(*) Применим метод интервалов. х=0, 2х2− 11х −4 =0, D = 153, х1 =  , х2 = .− + − + 0 Решение неравенства (*): (− ∞; ) (0; ).Решение исходного неравенства с учётом ОДЗ: [− ;) , (0; 2), (2; ). Ответ: [− ;) , (0; 2), (2; ). №14  Решим неравенство 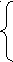 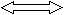 ОДЗ: 4х+15≥0, х ≥− ОДЗ: [−;−),(− ;  ),(;+ ∞). х ≠−, х ≠.  Сократим дробь на . получим неравенство , (*) Рассмотрим два случая:
Возведём обе части неравенства (*) в квадрат, получим: 4х+15≥4х2, 4х2 −4х −15≥0, 4х2 −4х −15=0, х1 =- , х2 = + − + − Решение неравенства: (− ∞; − ] [; + ∞). Условию х≥0 удовлетворяет числовой промежуток: [ ; + ∞). Учтём ОДЗ, получим: ( ; + ∞).
неравенство (*) верно для всех х из ОДЗ: [− ;−),(− ; ),(;+ ∞) . Учтём условие х < 0, получим [− ;−),(− ; 0).Решение исходного неравенства - [− ;−),(− ; 0), (; + ∞).Ответ: [− ;−),(− ; 0), (; + ∞). |