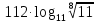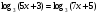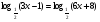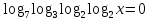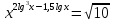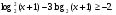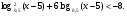Решение логарифмических уравнений и неравенств
 Скачать 193.32 Kb. Скачать 193.32 Kb.
|
 Тема: Решение логарифмических уравнений и неравенств. Тема: Решение логарифмических уравнений и неравенств.Класс: 11. Предмет: Алгебра и начала анализа. Тип урока: урок обобщения и систематизации знаний, умений и навыков по данной теме. Цели:
Задачи: Образовательная. Повторить теоретический материал. Обратить особое внимание на ОДЗ логарифмической функции. Систематизировать методы решения логарифмических уравнений, неравенств. Развивающая. Способствовать развитию математического языка, наглядно – образного мышления, коммуникативных умений учащихся. Воспитательная. Воспитание интереса к предмету посредством использования на уроке ПК; активности, умения общаться, общей культуре. Оборудование урока: - карточки с индивидуальными заданиями для самостоятельной работы; - карточки с заданиями для домашней работы; - карточки с заданиями для групп; - документ – камера - мультимедийный проектор, компьютер. - листы для самоконтроля Формы работы: - фронтальная; - работа в группах; - индивидуальная. Ход урока. 1.Орг.момент. Взаимное приветствие; проверка готовности учащихся к уроку, организация внимания. Сообщается тема урока и цели, подчеркивается актуальность данной темы для подготовки к ЕГЭ.2.Актуализация знаний. Учащиеся работают устно по упражнениям, представленным на экране с помощью проектора.
Вычислите
1 вариант Ответы 2 вариант
-Какое уравнение называют простейшим логарифмическим уравнением? Сколько решений имеет уравнение 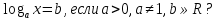 Какие методы решения логарифмических уравнений вам известны? Какие методы решения логарифмических уравнений вам известны?3. Работа в разноуровневых группах. Со всеми учащимися класса рассматриваются решения уравнений. 1. Решите уравнение log 2 4 + 2 log 2 х = log 2 (6х + 18) Учащиеся могут привести одно из представленных решений: а) Используя переход к равносильной системе: 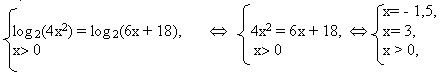 Ответ:3 б) Выполняя проверку найденных корней уравнения: 4х2 = 6х + 18, х = -1,5 или х = 3. Проверка. х = -1,5, log 24 + 2log 2(-1,5) = log 2(6(-1,5) + 18) - неверно; х = 3, log 24 + 2log 23 = log 2(6· 3 + 18), log 236 = log 236 - верно Ответ:3 -Далее первая группа учащихся самостоятельно выполняет задания №1. Группа № 1. 1. Решите уравнение (1-3). 1. log3 (2х - 4) = log3 (х + 3) 2. 2log4 x = log4 169 3. lg (2х2 - 4х + 12) = lgх + lg(х + 3). (1.7. 2 13. 3. 3; 4.) 2. Решите неравенство. log 0,2(3х - 5) > log 0,2(х + 1). (5/3< х< 3) -В это время учитель с учащимися второй и третьей группы рассматривает задания повышенного уровня сложности. 2. Решите уравнение lg(х + 4) + lg(2х + 3) = lg(1 - 2х). Решение. 1. Найдём ОДЗ: 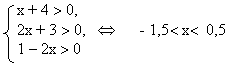 2. Преобразуем уравнение к виду: lg((х + 4)(2х + 3)) = lg(1 - 2х), 2х2 + 13х + 11 = 0, отсюда х1 = -1, х2 = -5,5. Так как - 1,5< х< 0,5, то х = -5,5 является посторонним корнем. Ответ: -1. Учащиеся второй группы приступают к самостоятельному выполнению заданий №1. Группа № 2 1.Решите уравнение (1-2). 1. log 2(х + 1) + log 2(х + 3) = 3. 2. log3 (x2 - 1) = 1 (1. 1. 2. -2; 2.). 2. Решите неравенство. lg2 x ≥ 9 (0; 0,001]U[1000;∞) -С учащимися третьей группы учитель рассматривает следующее уравнение: 3. Решите уравнение log1/3x log1/3 (3x-2)= log1/3 (3x-2) Решение. О. Д. З.: Log1/3x log1/3 (3x-2)= log1/3 (3x-2) Log1/3x log1/3 (3x-2) - log1/3 (3x-2)=0 Log1/3 (3x-2) ( log1/3 х-1)=0 Log1/3 (3x-2) =0 или log1/3 х-1=0 3х-2=1 log1/3x=1 3x=3 x= х=1 Ответ: х=1.
Группа № 3. 1.Решите уравнение log2(3x+1) log3x=2 log2(3x+1) 2. Решите неравенство. 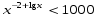 Решение заданий группы №3.1.Решение: О.Д.З.: 3x + 1>0 и х > 0 ↔ х > 0 log2 (3x+1)log3 x - 2log2(3x+1)=0; log2 (3x+1) (log3x -2) = 0; log2(3x+1)=0 или log3x=2 3x+1=1; x=32; 3x=0 x2=9 x1=0- посторонний корень. Ответ: х=9. 2. Решение. Прологарифмируем обе части неравенства по основанию10. Поскольку у = lg x функция монотонно возрастает, смысл неравенства при логарифмировании не меняется. 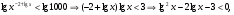 решим квадратное уравнение относительно решим квадратное уравнение относительно 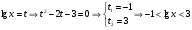 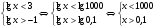 Ответ (0,1;1000). Учитель проверяет правильность выполнения заданий № 1 у учащихся первой и второй групп и если появляется необходимость, корректирует решения. По завершении проверки со всеми учащимися класса рассматривается следующее задание. 4. Решите неравенство log 0,5 (х + 1) > log 0,5 (2 - х). Решение. Функция у = log 0,5 х убывает. Поэтому: 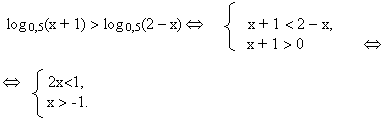 Ответ: (-1; 0,5). Учитель предлагает учащимся первой группы приступить к самостоятельному выполнению заданий № 2. С учащимися второй и третьей группы учитель рассматривает следующее задание. 5. Решите неравенство: 2 log3x -6 9 - log3 (x-2) ≥ 1 Решение. Перепишем неравенство в виде: 2log3 9 /log3 3(x-2) - log3 (x-2)≥1 ↔ 4/(1 + log3 (x - 2)) – log3 (x- 2) ≥ 1 Пусть log3 (x- 2) = a, тогда 4/ (a +1) – a ≥ 1 ↔ (4 – (a + 1)2)/(1 + a) ≥ 0 ↔ (a + 3)(a - 1)/(1 + a) ≤ 0 Далее воспользуемся методом интервалов. Получим a ≤ -3 или -1 ˂a ≤ 1. Oсталось решить совокупность неравенств: log3 ( x - 2) ≤ -3 или -1 ˂ log3 ( x - 2) ≤ 1 ↔ 0 ˂x - 2≤ 1/27 или 1/3 ˂ x -2 ≤ 3 ↔ 2 ˂ x ≤ 55/27 или 7/3 ˂ x ≤ 5. Ответ: (2; 55/27] U( 7/3; 5] Далее вторая и третья группы учащихся самостоятельно выполняют задания № 2. Пока учащиеся второй и третьей группы выполняют задания, учитель проверяет решения учащихся первой группы, комментирует их при необходимости, после чего проверяются ответы у учащихся второй и третьей групп. 4. Физминутка. Сцепили руки в “замок”, вытянули перед собой, подняли вверх и хорошо потянулись. Врачи утверждают, что в этот момент выделяется “фермент счастья”. 5. Разноуровневая самостоятельная работа (Слайд на экране и карточки у каждого ученика). Учащимся предлагается оценить свои возможности и выбрать уровень заданий базовый А, повышенный В. 1 вариант 2 вариант А. 1.Решите уравнение А. 1.Решите уравнение log 2 (x + 1) = 4 lg (x - 10) =1 2. Решите неравенство 2. Решите неравенство log 5 (2х + 1) ≥ log 5 (х - 1). 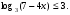 B. B. 1.Решите уравнение 1.Решите уравнение 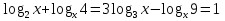 2. Решите неравенство 2. Решите неравенство log20,2 х - 5 log 0,2 х < -6 log2 0,1 х + 3 log 0,1 х > 4. Выполнив работу, учащиеся сдают ее на проверку. На экран выводятся ответы и краткое решение. Учащимся предлагается проверить и оценить свою работу, выставив оценку за самостоятельную работу. Ответы: 1 вариант. А. 1. 15; 2.(1; ∞) В. 1. 4, 2; 2. (0,008; 0,04) 2 вариант. А. 1. 20; 2. (- 5; 1,75) В. 1. 9, 1/3. 2. (0; 0,1)U(10000; ∞) 6. Домашнее задание. карточки с заданиями для домашней работы.
7. Итог урока. Рефлексия Итак, мы сегодня с вами решали логарифмические уравнения и неравенства. А теперь давайте обобщим, какие методы решения мы применяли? Выставление оценок по количеству «+» в тетради, за решение на доске и по карточкам. Определение результативности работы учащихся. Наш урок подошел к концу. Достигли ли мы поставленных целей? Готовясь к экзамену, никогда не думай, что не справишься с заданием, а, напротив, мысленно рисуй себе картину успеха и тогда у тебя обязательно все получится! Группа № 1. 1. Решите уравнение (1-3). 1. log 2(х + 1) + log 2(х + 3) = 3. 2. log3 (x2 – 1) = 1 3. lg (2х2 - 4х + 12) = lgх + lg(х + 3). (1.1. 2. 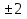 . 3.3; 4.) . 3.3; 4.)2. Решите неравенство. log 0,2(3х - 5) > log 0,2(х + 1). (5/3< х< 3) Группа № 2 1.Решите уравнение (1-2). 1. log 4(х2 - 1) - log 4(х -1)2 = log 4│2 - х│. 2. log 2х4 + log 2х2 = 6. (1.2+ 2. Решите неравенство. lg2 x ≥ 9 (0; 0,001]U[1000;∞) Группа № 3. 1.Решите уравнение 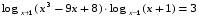 2. Решите неравенство. 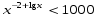 1 вариант 2 вариант А. 1.Решите уравнение А. 1.Решите уравнение log 2 (x + 1) = 4 lg (x - 10) =1 2. Решите неравенство 2. Решите неравенство log 5 (2х + 1) 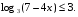 B. B. 1.Решите уравнение 1.Решите уравнение 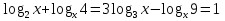 2. Решите неравенство 2. Решите неравенство log20,2 х - 5 log 0,2 х < -6 log2 0,1 х + 3 log 0,1 х > 4. C. C. 1.Решите уравнение 1.Решите уравнение log3x + 7 (5x + 3) + log5x + 3(3x + 7) = 2 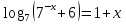 2. Решите неравенство 2. Решите неравенство 1/(5 -lg х ) + 2/(1 + lg х) < 1. 1/(lоg5(3 - 2х)) - 1/(4 - lоg5(3 - 2 х)) < 0. 1 вариант 2 вариант А. 1.Решите уравнение А. 1.Решите уравнение log 2 (x + 1) = 4 lg (x - 10) =1 2. Решите неравенство 2. Решите неравенство log 5 (2х + 1) 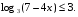 B. B. 1.Решите уравнение 1.Решите уравнение 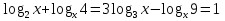 2. Решите неравенство 2. Решите неравенство log20,2 х - 5 log 0,2 х < -6 log2 0,1 х + 3 log 0,1 х > 4. C. C. 1.Решите уравнение 1.Решите уравнение log3x + 7 (5x + 3) + log5x + 3(3x + 7) = 2 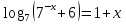 2. Решите неравенство 2. Решите неравенство 1/(5 -lg х ) + 2/(1 + lg х) < 1. 1/(lоg5(3 - 2х)) - 1/(4 - lоg5(3 - 2 х)) < 0. 1 вариант 2 вариант А. 1.Решите уравнение А. 1.Решите уравнение log 2 (x + 1) = 4 lg (x - 10) =1 2. Решите неравенство 2. Решите неравенство log 5 (2х + 1) 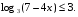 B. B. 1.Решите уравнение 1.Решите уравнение 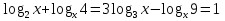 2. Решите неравенство 2. Решите неравенство log20,2 х - 5 log 0,2 х < -6 log2 0,1 х + 3 log 0,1 х > 4. C. C. 1.Решите уравнение 1.Решите уравнение log3x + 7 (5x + 3) + log5x + 3(3x + 7) = 2 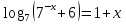 2. Решите неравенство 2. Решите неравенство 1/(5 -lg х ) + 2/(1 + lg х) < 1. 1/(lоg5(3 - 2х)) - 1/(4 - lоg5(3 - 2 х)) < 0.
ДИАГНОСТИЧЕСКАЯ КАРТА УЧАЩЕГОСЯ. ВАРИАНТ 1. ВАРИАНТ 2. Выполнял:__________________________________________________
ДИАГНОСТИЧЕСКАЯ КАРТА УЧАЩЕГОСЯ. ВАРИАНТ 1. ВАРИАНТ 2. Выполнял:__________________________________________________
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
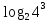 1)
1) 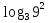
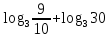 2)
2) 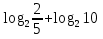
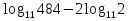 3)
3) 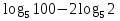
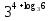 4)
4) 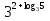
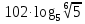 5)
5)