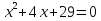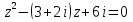Решение квадратных уравнений с действительными и комплексными коэффициентами
 Скачать 23.98 Kb.
|
| Решение квадратных уравнений с действительными и комплексными коэффициентами. Квадратное уравнение с действительными или комплексными коэффициентами a, b, c всегда имеет 2 корня. В зависимости от значения дискриминанта D = b2 − 4ac уравнения с действительными коэффициентами возможны следующие случаи:
Если коэффициенты квадратного уравнения комплексные, то возможны 2 случая:
Определение. Число ω называется квадратным корнем из комплексного числа z, если ω2 = z. Теорема. Пусть z = a + b  i – отличное от нуля комплексное число. Тогда существуют два взаимно противоположных комплексных числа, квадраты которых равны z. Если b≠0, то эти числа выражаются формулой: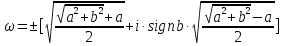 где  Например,  Решить уравнение: Задания для работы в классе: Виленкин Н. Я. Алгебра и математический анализ 11 класс Стр. 188, № 338, 337, 339 (нечетные цифры) Домашнее задание. № 338, 337, 339 (четные цифры) Решение квадратных уравнений с действительными и комплексными коэффициентами. Квадратное уравнение с действительными или комплексными коэффициентами a, b, c всегда имеет 2 корня. В зависимости от значения дискриминанта D = b2 − 4ac уравнения с действительными коэффициентами возможны следующие случаи:
Если коэффициенты квадратного уравнения комплексные, то возможны 2 случая:
Определение. Число ω называется квадратным корнем из комплексного числа z, если ω2 = z. Теорема. Пусть z = a + b i – отличное от нуля комплексное число. Тогда существуют два взаимно противоположных комплексных числа, квадраты которых равны z. Если b≠0, то эти числа выражаются формулой: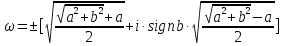где Например, Решить уравнение: Задания для работы в классе: Виленкин Н. Я. Алгебра и математический анализ 11 класс Стр. 188, № 338, 337, 339 (нечетные цифры) Домашнее задание. № 338, 337, 339 (четные цифры) |
