|
Разработка урока по математике «Законы арифметических действий. Распределительный закон»
Муниципальное бюджетное образовательное учреждение
«Средняя общеобразовательная школа №3»
«Современный урок –
как основа эффективного
и качественного образования
школьников»
Методическая разработка урока по математике
«Законы арифметических действий. Распределительный закон»
для учащихся 5 классов
Автор: Грачева Наталья Павловна,
учитель математики,
стаж работы 20 лет,
высшая квалификационная категория
г. БИЙСК
Пояснительная записка
Тема урока «Законы арифметических действий. Распределительный закон».
Тип урока – урок изучения новых знаний.
Форма урока – урок-исследование.
Преподавание математики в 5-м классе ведется по учебнику И.И. Зубарева, А.Г.Мордкович «Математика, 5 класс». По учебному плану на изучение математики
в 5-м классе отводится 5 часов в неделю (170 часов в год).
В соответствии с программой изучается раздел «Натуральные числа». В рамках этого раздела содержится тема «Законы арифметических действий». Урок изучения новых знаний «Законы арифметических действий» является вторым уроком в данном параграфе.
Урок построен на основе деятельностного подхода и технологии проблемного обучения, что предполагает максимальное использование собственной исследовательской активности ученика по определению, поиску и нахождению нового знания. В ходе урока планируются не только предметные результаты обучения, но и метапредметные, и личностные.
Основной метод, применяемый на уроке, – метод исследования, предполагающий построение обучения как творческого процесса открытия ребенком нового знания. Способы организации деятельности учащихся на уроке – парная и индивидуальная работа.
Цели урока (формирование УУД):
Личностные:
формирование у учащихся готовности и способности к самообразованию на основе мотивации к обучению и познанию;
формирование уважительного и доброжелательного отношения к другому человеку, его мнению;
формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками в процессе учебно-исследовательской деятельности.
Метапредметные: развитие у учащихся умений:
находить необходимую информацию в тексте;
анализировать информацию;
формулировать гипотезы;
устанавливать причинно-следственные связи, проводить умозаключение и делать выводы;
соотносить свои действия с планируемыми результатами.
Предметные:
формирование представлений учащихся о законах арифметических действий;
развитие умений применять изученные законы арифметических действий; записывать словесную форму закона арифметических действий на математическом языке.
Этапы урока.
I этап. Актуализация знаний.
II этап. Постановка учебной задачи.
III этап. «Открытие нового знания» (исследование).
IV этап. Первичное закрепление.
V этап. Рефлексия.
VI этап. Домашнее задание.
Ход урока.
I, II этапы. Актуализация знаний. Постановка учебной задачи.
Цель: создание проблемной ситуации, которая вытекает из-за невозможности выполнения задания (не хватает определенных знаний, «интеллектуальный разрыв»).
Деятельность Учителя
|
Деятельность Ученика
|
Слайд
|
Формируемые УУД
на данном этапе
|
Здравствуйте, ребята! Садитесь!
|
|
Приложение №2
№3
|
Личностные:
формирование у учащихся готовности к самообразованию на основе мотивации к обучению.
Предметные:
формирование представлений учащихся
о законах арифметических действий.
Метапредметные:
поиск нового способа действия в измененной ситуации в связи с невозможностью использования уже освоенных способов (познавательные УУД); целеполагание
|
Ребята, давайте начнем наш урок со стихотворения.
( пропущено слово Гаусса).
- О ком идет речь в этом стихотворении?
- Чьим именем потомки назовут эпоху XIX века?
- Ребята, а почему мы опять возвращаемся к имени великого математика Фридриха Гаусса?
|
Дети читают стихотворение и замечают, что не все слова есть в предложении.
(Ученики отвечают на вопросы учителя).
Предполагаемые ответы
- Речь идет о великом немецком математике Фридрихе Гауссе.
Потому что на прошлом уроке мы познакомились с «крупицей» его открытий в математике «Законы арифметических действий».
|
- А какие законы арифметических действий у нас были на прошлых уроках?
|
Мы открывали и узнали, законы сложения и законы умножения.
|
№4
|
- А как называются эти законы (полное название)?
|
Переместительный законы сложения и умножения.
Сочетательный законы сложения и умножения.
|
- Давайте вспомним эти законы на математическом языке и словесную форму.
|
Работа по слайду. Ученики называют закон, номер формулы, соответствующую этому закону и словесную формулировку.
|
Где и для чего используются законы арифметических действий?
|
При нахождении значений числовых выражений, для рационального счета. (быстроты счета, упрощения счета)
|
Вот и давайте посмотрим, как эти законы помогают вам быстро вычислять. Предлагаю выполнить задание: математический диктант (по вариантам).
|
Дети вычисляют в уме. Записывают ответ в тетрадь. Проверяют ответы по слайду.
|
№5
|
Быстро можно вычислить, используя законы?
|
Да. Правильно вот для этого мы их и изучаем.
|
Следующее задание: хорошо, с этими выражениями вы справились быстро. Найдите значения следующих выражений.
|
У ребят появляется затруднение, так как эти выражения на применение распределительного закона умножения. (интеллектуальный разрыв)
|
№5 продолжение
|
- Ребята, а в чем у вас затруднение?
- А почему мы не можем вычислить?
|
Говорят, что эти выражения нельзя вычислить, используя законы известные.
|
|
- А как тогда быть, что делать? Вычислять, то нужно!
|
Могут предложить по действиям.
Могут предложить узнать новый закон.
|
№6
Приложение №2
|
- сформулируйте цели нашего урока. Что мы сегодня на уроке будем делать? Узнавать, открывать, вычислять?
|
Ребята, формулируют цели урока.
|
Сформулируйте тему нашего сегодняшнего урока. Хорошо, молодцы.
Открываем тетради, записываем число и тему урока «Законы арифметических действий».
|
Формулируют тему.
Записывают в тетрадь тему урока.
|
Перед вами на столах лежат мультифоры достаньте карточку №1 с названием «Исследование». (предлагаю ученикам выполнить задания в парах). Сделайте вывод и запишите прямо на этих же листах выражения в буквенном виде.
|
Дети вычисляют, выдвигают предположения (гипотезы).
Делают выводы.
Записывают формулы в тетрадь.
|
|
Результат: выдвижение гипотез о записи закона в буквенном виде.
III этап. «Открытие нового знания» (исследование).
Цель: доказательство выдвинутых предположений и представление результатов работы пар всему классу.
Учащиеся работают в парах.
Карточка №1
«Исследование»
1). Вычислите.
3 90 + 3 10 3 (90 + 10)
7 50 – 7 30 7 (50 – 30)
5 13 + 5 77 5 (13 + 77)
2). Сравните результаты, в каждой строке левого и правого столбцов.
Что вы замечаете?
3). В каком столбце быстрее вычислить в правом или в левом?
4). Замените в данных выражениях в каждой строке одинаковые числа буквой а, а другие числа буквами b и c.
5). Запишите эти выражения в тетрадь. Сколько равенств можно записать?
После заполнения таблицы, учащиеся делают вывод. Записывают формулы закона в буквенном виде.
Формируемые УУД на данном этапе:
Личностные:
формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками в процессе исследовательской деятельности (коммуникативные УУД).
Предметные:
формирование представлений учащихся о законах арифметических действий.
Метапредметные:
развитие у учащихся умений планировать собственную деятельность в соответствии с поставленной задачей, анализировать информацию, формулировать гипотезы (регулятивные УУД);
устанавливать причинно-следственные связи, проводить умозаключение и делать выводы (познавательные УУД).
Результат: подтверждение или опровержение гипотез, выдвинутых детьми на первом этапе.
Деятельность Учителя
|
Деятельность Ученика
|
Слайд
|
Формируемые УУД
|
Итак, проверяем.
Какой вывод у вас получился?
|
Учащиеся по слайду проверяют запись формул.
|
№7
|
Метапредметные:
развитие у учащихся умений анализировать информацию, формулировать гипотезы;
создавать обобщения, устанавливать причинно-следственные связи, проводить умозаключение и делать выводы;
соотносить свои действия с планируемыми результатами.
Предметные:
формирование представлений учащихся о распределительном законе.
|
Итак, что же мы с вами получили?
Что показывает это свойство?
|
Делают вывод: это свойство еще один закон арифметических действий.
|
|
Пока у нас запись только на математическом языке, а как это свойство сказать словесно?
Сложно, тогда в мультифорах лежит правило, составьте из разрезанных частей словесную форму.
|
Пробуют.
Составляют. Читают вслух.
|
Приложение №3
|
Выводы, которые получили ребята
Давайте проверим ваши открытия, правильно ли сформулировали это свойство?
Итак, мы, с вами теперь знаем запись этого свойства на математическом языке и словесную форму.
А что мы так и не знаем до пор?
|
Дети открывают учебник на стр. 66 ( 2 абзац). Читают вслух правила. Сравнивают со своими результатами.
Как называется этот закон.
|
|
А сейчас «физкультминутка»!!!!!
|
|
№8-№10
|
Молодцы!!!
|
|
- А теперь за работу.
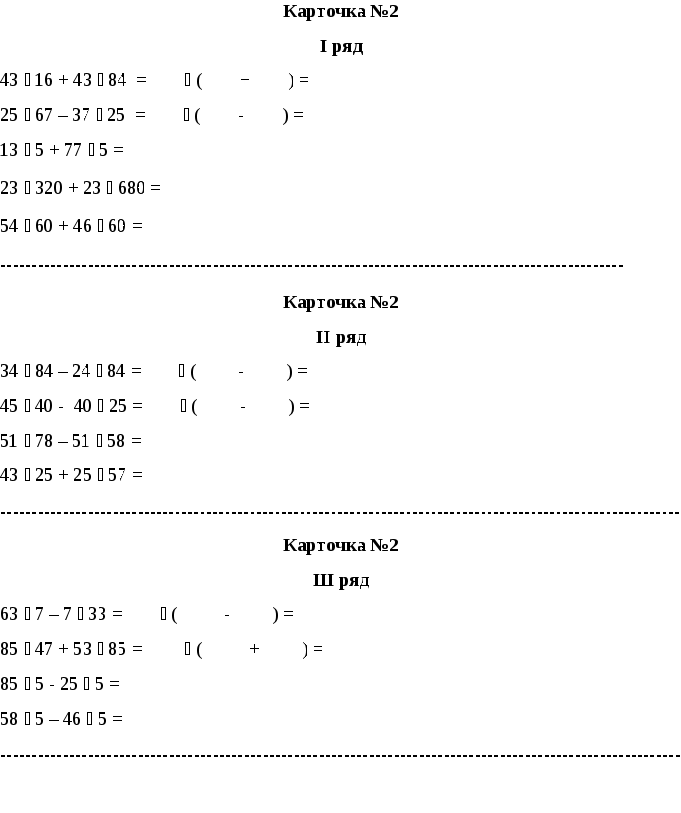
Достаньте карточку №2.
Вычислите (работайте в парах)
|
Вычисляют в парах по рядам.
Проверяем по слайду с доски.
|
№11
Приложение №4
|
|
Результат: в ходе исследования учащиеся вывели запись закона на математическом языке и словесную форму закона. В результате первичного закрепления они узнали название этого закона и научились выносить общий множитель за скобки.
|
IV, V этапы. Первичное закрепление. Рефлексия.
Цель: использование новых знаний при решении частных задач и осознание учащимися своей УД, самооценка результатов своей деятельности.
Деятельность Учителя
|
Деятельность Ученика
|
Слайд
|
Формируемые УУД
|
Первичное закрепление по слайду
|
Выполняют на этих же листах, где задание.
|
|
|
Молодцы!!!
Итак, быстро и просто вычислять, если использовать распределительный закон?
Это еще раз показывает, для чего мы с вами изучаем законы арифметических действий?
|
|
№ 11
|
Предметные:
формирование представлений учащихся о распределитеном законе умножения относительно сложения и вычитания;
развитие умений применять изученный закон при устном счете.
|
- А ну-ка вернемся к примерам в начале урока. Вычислите и запишите ответы в тетрадь.
Молодцы!!!
|
|
№ 13
|
Итак, ребята, что нового для себя вы открыли на уроке?
Как он называется?
А как он читается словесно?
Ребята. а у меня к вам еще вопрос, вот на прошлом уроке мы открывали с вами законы:
- переместительный закон сложения и умножения;
- сочетатеный закон сложения и умножения.
- А распределительный закон это закон какого арифметического действия?
Молодцы!!!
А сейчас каждый из вас подумает, что у него на уроке сегодня получилось. А может быть все, получилось, и формулы получил сам. Правильно. И открыл сам признак делимости. И при решении новых заданий все получилось. Или что-то немного не получилось, где-то. Все подумали, а сейчас возьмите лесенку «успеха», подпишите фамилию и нарисуйте себя, человечком на той ступеньке, какую вы сами себе сегодня определили.
|
Новый закон арифметических действий.
Проговаривают еще раз название, словесную форму, смотрим формулы на доске.
Могут сказать и сложения и вычитания и умножения. Заостряю внимание, что последнее выполняющееся действие умножение. Поэтому закон умножения относительно сложения и вычитания.
Рисуют себя на лестнице «успеха»
|
№ 12
|
|
Задаю вопросы по лесенке «успеха»
|
По желанию ученики высказываются.
|
№ 14
Приложение №5
|
|
Ребята, на протяжении всего урока я за вами наблюдала, и мне хотелось бы прочитать вам такое высказывание.
А почему, как вы думаете, мне захотелось вам ее прочитать?
Правильно, молодцы.
На этом наш урок заканчивается, но на следующих уроках вас ждут опять новые открытия. До свидания! Желаю успеха в выполнении домашнего задания!
|
Ребята высказывают предположения.
|
№ 15
|
|
Результат: актуализация знаний в ходе решения задач, и выполнении математического диктанта.
VI этап. Домашнее задание. § 13; стр. 66 № 223 (устно); № 219 и № 220 (II столбик).
Приложение №1

Приложение №2
Карточка №1
«Исследование»
1). Вычислите.
3 90 + 3 10 3 (90 + 10)
7 50 – 7 30 7 (50 – 30)
5 13 + 5 77 5 (13 + 77)
2). Сравните результаты, в каждой строке левого и правого столбцов.
Что вы замечаете?
3). В каком столбце быстрее вычислить в правом или в левом?
4). Замените в данных выражениях в каждой строке одинаковые числа буквой а, а другие числа буквами b и c.
5). Запишите эти выражения в тетрадь.
Сколько равенств можно записать?
Приложение №3
Сумму двух или нескольких произведений,
|
содержащих одинаковый множитель,
|
можно заменить произведением этого множителя
|
на сумму остальных множителей.
|
Приложение № 4
Приложение № 5

|
|
|
 Скачать 133.21 Kb.
Скачать 133.21 Kb.

