|
Рабочая программа учебного курса по математике для 9-го класса. Пояснительная записка
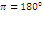 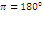 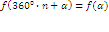 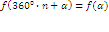 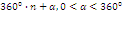 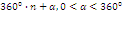 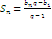 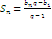 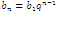 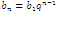 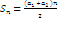 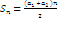 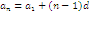 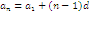 Кочурова Екатерина Игоревна учитель МКОУ СОШ села Синегорье Нагорского района Кировской области. Кочурова Екатерина Игоревна учитель МКОУ СОШ села Синегорье Нагорского района Кировской области.
Рабочая программа учебного курса по математике для 9-го класса.
Пояснительная записка
Рабочая программа по математике для 9 класса составлена на основе Примерной программы основного общего образования с учетом требований федерального компонента государственного стандарта общего образования и с учетом программ для общеобразовательных школ, гимназий, лицеев (Кузнецова Г.М., Миндюк Н.Г. Математика 5-11 кл.- М.: Дрофа, 2009).
Учебник «Алгебра 9», авторы Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова М.: Просвещение, 2007 и учебник «Геометрия 7-9», авторы Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. М.: Просвещение, 2007.
Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека. Алгебра нацелена на формирование математического аппарата для решения задач из математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др.).
В задачи обучения математики входит:
овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;
овладение навыками дедуктивных рассуждений;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, необходимой, в частности, для освоения курса информатики;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и т.д.);
воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.
Курс алгебры построен в соответствии с традиционными содержательно-методическими линиями: числовой, функциональной, алгоритмической, уравнений и неравенств, алгебраических преобразований. В курсе алгебры 9-го класса продолжается систематизация и расширение сведений о функциях. Важное место занимает изучение квадратичных функций и их свойств, а также частных видов: 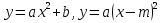 . Формируются умения решать неравенства вида: . Формируются умения решать неравенства вида: 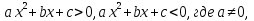 которые опираются на сведения о графике квадратичной функции. На этапе 9-го класса завершается изучение рациональных уравнений с одной переменной. Дается понятие целого рационального уравнения и его степени. Особое внимание уделяется решению уравнений третьей и четвертой степени с помощью разложения на множители и введения вспомогательной переменной, что широко используется в дальнейшем при решении тригонометрических, логарифмических и других видов уравнений. Рассматриваются системы, содержащие уравнения второй степени с двумя неизвестными. Даются первые знания об арифметической и геометрической прогрессиях, как о частных видах последовательностей. Изучая формулу нахождения суммы которые опираются на сведения о графике квадратичной функции. На этапе 9-го класса завершается изучение рациональных уравнений с одной переменной. Дается понятие целого рационального уравнения и его степени. Особое внимание уделяется решению уравнений третьей и четвертой степени с помощью разложения на множители и введения вспомогательной переменной, что широко используется в дальнейшем при решении тригонометрических, логарифмических и других видов уравнений. Рассматриваются системы, содержащие уравнения второй степени с двумя неизвестными. Даются первые знания об арифметической и геометрической прогрессиях, как о частных видах последовательностей. Изучая формулу нахождения суммы 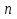 первых членов арифметической прогрессии первых членов арифметической прогрессии 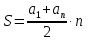 и формулу суммы и формулу суммы 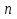 первых членов геометрической прогрессии первых членов геометрической прогрессии 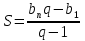 , целесообразно уделить внимание заданиям, связанным с непосредственным применением этих формул. Из курса геометрии продолжается изучение синуса, косинуса и тангенса острого угла прямоугольного треугольника. Вводится понятие котангенса угла. Изучаются свойства синуса, косинуса, тангенса и котангенса, которые находят применение в преобразованиях тригонометрических выражений. Специальное внимание уделяется переходу от радианной меры угла к градусной мере и наоборот. Центральное место занимают формулы, выражающие соотношения между тригонометрическими функциями одного и того же аргумента. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов. , целесообразно уделить внимание заданиям, связанным с непосредственным применением этих формул. Из курса геометрии продолжается изучение синуса, косинуса и тангенса острого угла прямоугольного треугольника. Вводится понятие котангенса угла. Изучаются свойства синуса, косинуса, тангенса и котангенса, которые находят применение в преобразованиях тригонометрических выражений. Специальное внимание уделяется переходу от радианной меры угла к градусной мере и наоборот. Центральное место занимают формулы, выражающие соотношения между тригонометрическими функциями одного и того же аргумента. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
Геометрия – один из важнейших компонентов математического образования. Она необходима для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, развития пространственного воображения и интуиции, математической культуры, эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
В курсе геометрии 9-го класса формируется понятие вектора. Особое внимание уделяется выполнению операций над векторами в геометрической форме. Учащиеся дополняют знания о треугольниках сведениями о методах вычисления элементов произвольных треугольниках, основанных на теоремах синусов и косинусов. Даются систематизированные сведения о правильных многоугольниках, об окружности, вписанной в правильный многоугольник и описанной. Особое место занимает решение задач на применение формул. Даются первые знания о движении, повороте и параллельном переносе. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
Программой отводится на изучение математики по 6 уроков в неделю, что составляет 210 часов в учебный год. Из них контрольных работ 14 часов, которые распределены по разделам следующим образом: «Квадратичная функция» 2 часа, «Уравнения и системы уравнений» 1 час, «Арифметическая и геометрическая прогрессии» 2 часа, «Степень с рациональным показателем» 1 часа, «Тригонометрические выражения и их преобразования» 1 часа, «Метод координат» 2 часа, «Соотношение между сторонами и углами треугольника» 2 часа, «Длина окружности и площадь круга» 1 час, «Движения» 1 час и 1 час отведен на итоговую административную контрольную работу.
Для более широкого и глубокого знакомства с математикой введен курс «Элементы статистики и теории вероятностей» в количестве 8 часов. На этом этапе продолжается решение задач путем перебора возможных вариантов, изучается статистический подход к понятию вероятности. Формируются умения вычислять вероятности с помощью формул комбинаторики. Особое внимание уделяется правилу сложения и умножения вероятностей.
Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.
Количество часов по темам изменено в связи со сложностью тем.
Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных работ и математических диктантов (по 10 - 15 минут) в конце логически законченных блоков учебного материала. Итоговая аттестация предусмотрена в виде административной контрольной работы.
Домашнее задание описано на блок уроков. По ходу работы, в зависимости от темпа прохождение материала номера заданий распределяются по урокам так, что по окончании изучения блока все задания выполнены учащимися в обязательном порядке.
Для развития устойчивого интереса к учебному процессу, уроки математики интегрируются с уроками информатики. Некоторые разделы алгебры закрепляются посредством тестов на ПК, которые разработали сами учащиеся. Для этого используется пакет прикладных программ Microsoft Office и УМК Живая математика – это компьютерная система моделирования, исследования и анализа широкого круга задач математики. Программа Живая Математика помогает конструировать интерактивные математические модели, давая начальные представления о понятиях формы тела, числах и т.п. Живая Математика помогает поставить мысленный эксперимент вида "что если?".
Электронные учебники используются в качестве виртуальных лабораторий при проведении практических занятий, уроков введения новых знаний. В них заключен большой теоретический материал, много тренажеров, практических и исследовательских заданий. На любом из уроков возможно использование компьютерных устных упражнений, применение тренажера устного счета, что активизирует мыслительную деятельность учащихся, развивает вычислительные навыки.
Требования к уровню подготовки учащихся.
В результате изучения курса алгебры 9-го класса учащиеся должны уметь:
строить график квадратичной функции; находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак;
понимать содержательный смысл важнейших свойств функции; по графику функции отвечать на вопросы, касающиеся её свойств;
бегло и уверенно выполнять арифметические действия с рациональными числами; вычислять значения числовых выражений, содержащих степени и корни;
решать простейшие системы, содержащие уравнения второй степени с двумя переменными; решать текстовые задачи с помощью составления таких систем;
решать квадратные уравнения и уравнения, сводящиеся к ним, используя приемы и формулы для решения различных видов квадратных уравнений, графический способ решения уравнений;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
вычислять значения тригонометрических функций по известному значению одной из них; выполнять несложные преобразования тригонометрических выражений;
использовать приобретенные знания, умения, навыки в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе с использованием при необходимости справочной литературы, калькулятора, компьютера;
устной прикидки, и оценки результата вычислений, проверки результата вычислений выполнением обратных действий;
интерпретации результата решения задач.
В результате изучения курса геометрии 9-го класса учащиеся должны уметь:
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;
вычислять значения геометрических величин (длин, углов, площадей), в том числе: определять значение тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них; находить стороны, углы и площади треугольников, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задания, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве.
Сокращения, используемые в рабочей программе:
Типы уроков:
УОНМ — урок ознакомления с новым материалом.
УЗИМ — урок закрепления изученного материала.
УПЗУ — урок применения знаний и умений.
УОСЗ — урок обобщения и систематизации знаний.
УПКЗУ — урок проверки и коррекции знаний и умений.
КУ — комбинированный урок.
Виды контроля:
ФО — фронтальный опрос.
ИРД — индивидуальная работа у доски.
ИРК — индивидуальная работа по карточкам.
СР — самостоятельная работа.
ПР — проверочная работа.
МД — математический диктант.
Т – тестовая работа.
Календарно-тематическое планирование
№
|
Наименование раздела программы
|
Тема урока
|
Кол-во часов
|
Тип урока
|
Элементы содержания образования
|
Требования к уровню подготовки обучающихся
|
Вид кон-троля
|
Элементы доп-ного содержания
|
Дата проведения урока
|
план
|
факт
|
I
|
Квадратичная функция
|
|
31
|
|
|
|
|
|
|
|
1-2
|
Функции и их графики.
|
2
|
КУ
|
независимая, зависимая переменная, функция, график функции
|
-уметь находить по значению аргумента значение функции и наоборот
|
ФО [1], стр.4 ?
|
|
|
|
3-4
|
Область определения и область изменения.
|
2
|
КУ УПЗУ
|
функция, область определения и область изменения
|
-уметь находить область определения и область значения функции;
-уметь строить более сложные графики функций
|
ФО [1], стр.8 ?
ПР [3], С-1
|
|
|
|
5-7
|
Свойства функций.
|
3
|
КУ
УОНМ
|
нули функции, возрастающая и убывающая функция
|
-уметь определять нули функции, промежутки возрастания и убывания
|
ФО [1], стр.10?
ИРД
|
|
|
|
8-10
|
Квадратный трехчлен и его корни.
|
3
|
УПЗУ КУ
УОНМ
|
квадратный трехчлен, его корни
|
-уметь находить корни квадратного трехчлена
|
ФО [1], стр.18 ?
СР [3], С-5
|
|
|
|
11-12
|
Разложение квадратного трехчлена на множители.
|
2
|
УОНМ УЗИМ
|
корни квадратного трехчлена, разложение на множители
|
-уметь находить корни квадратного трехчлена;
-уметь раскладывать на множители квадратный трехчлен
|
ФО [1], стр.22?
СР [3], С-6
|
|
|
|
13-15
|
Функция 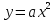 . .
|
3
|
КУ УОНМ
|
функция, график функции, свойства функции
|
-уметь строить график функции 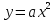 ; ;
-правильно читать график
|
ФО [1], стр.28
ИРД
|
|
|
|
16-17
|
Графики функций 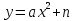 и и 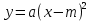 . .
|
2
|
КУ
УПЗУ
|
график функции, параллельный перенос
|
-уметь строить график функции, используя преобразования графиков
|
ФО [1], стр.32 ?
СР [3], С-7
|
УМК Живая математика
|
|
|
18-21
|
Построение графика квадратичной функции.
|
4
|
УОНМ
УПЗУ
|
квадратичная функция, парабола, вершина параболы, ветви параболы
|
-знать алгоритм построения графика квадратичной функции;
-уметь находить координаты вершины параболы
|
ФО[1],
стр.36 ?
СР [3], С-8
|
УМК Живая математика
|
|
|
22
|
Контрольная работа №1.
|
1
|
|
|
уметь применять полученные знания по теме в комплексе
|
|
|
|
|
23-25
|
Решение неравенств второй степени.
|
3
|
КУ УОНМ
УПЗУ
|
неравенства второй степени с одной переменной
|
-знать и понимать алгоритм решения неравенств;
-уметь правильно найти ответ в виде числового промежутка
|
ФО [1], стр.41 ?
ИРД
|
|
|
|
26-29
|
Метод интервалов.
|
4
|
КУ УОСЗУПЗУ
|
нули функции, метод интервалов
|
-знать алгоритм решения неравенств методом интервалов;
-уметь решать неравенства, используя метод интервалов
|
ФО [1], стр.46 ?
ИРД
СР[3], С-10
|
|
|
|
30
|
|
Обобщающий урок.
|
1
|
КУ
|
свойства функций, график функций, разложение на множители квадратного трехчлена
|
-четко знать алгоритм построения графика функции, свойства функции;
-уметь строить графики функций;
-уметь решать неравенства методом интервалов
|
ФО
|
|
|
|
31
|
Контрольная работа №2.
|
1
|
|
|
-уметь применять полученные знания по теме в комплексе
|
[3], КР-1
|
|
|
|
II
|
Метод координат
|
|
14
|
|
|
|
|
|
|
|
32-34
|
Координаты вектора.
|
3
|
КУ
УОНМ
|
координаты вектора, координаты результатов операций над векторами, коллинеарные вектора
|
-уметь находить координаты вектора по его разложению и наоборот;
-уметь определять координаты результатов сложения, вычитания, умножения на число
|
ФО [1], стр.249 ?1-8
ИРД
СР[2], С-1
|
УМК Живая математика
CD ИМ/Виртуальная лаборатория «Координатная плоскость».
|
|
|
35-37
|
Решение задач.
Простейшие задачи в координатах.
|
3
|
КУ
КУ УПЗУ
|
координаты вектора, координаты результатов операций над векторами
радиус-вектор, координата вектора, метод координат, координата середины отрезка, длина вектора, расстояние между двумя точками
|
-уметь применять знания при решении задач в комплексе
-уметь определять координаты радиус-вектора;
-уметь находить координаты вектора через координаты его начала и конца;
- уметь вычислять длину вектора по его координатам, координаты середины отрезка и расстояние между двумя точками
|
ФО [1],
ИРД
ФО [1], стр.249 ? 9-13
ИРД
ИРК
СР[2], С-2
|
УМК Живая математика
CD ИМ/Виртуальная лаборатория «Координатная плоскость».
|
|
38
|
Контрольная работа №3.
|
1
|
|
|
-уметь применять полученные знания в комплексе при решении задач на определение координат вектора, на определение вектора суммы, разности, произведения
|
[3], КР-1
|
|
|
|
39-40
|
Уравнение окружности.
|
2
|
УЗИМ
|
уравнение окружности
|
-знать уравнение окружности;
-уметь решать задачи на применение формулы
|
ФО [1], стр.249 ? 16,17
ИРД
|
УМК Живая математика
|
|
|
41-42
|
Уравнение прямой.
|
2
|
УОНМ
|
уравнение прямой
|
-знать уравнение прямой;
-уметь решать задачи на применение формулы
|
ФО [1], стр.249 ? 18-21
ИРД
СР[2], С-3
|
УМК Живая математика
|
|
|
43-44
|
Решение задач.
|
2
|
КУ УПЗУ
|
уравнение окружности и прямой
|
-знать уравнения окружности и прямой;
-уметь решать задачи
|
ФО
ИРД
ИРК
|
|
|
|
45
|
Контрольная работа №4.
|
1
|
|
|
-уметь решать простейшие задачи в координатах;
-уметь решать задачи на составлении уравнений окружности и прямой
|
[3], КР-2
|
|
|
|
|
|
II1
|
Уравнения и системы уравнений
|
|
22
|
|
|
|
|
|
|
|
46-49
|
Целое уравнение и его корни.
|
4
|
КУ
УПЗУ УЗИМ УПКЗУ
|
целое уравнение, равносильные уравнения, степень уравнения, корни уравнения, графический способ решения уравнений
|
-уметь определять степень уравнения;
-уметь решать уравнения третьей и более степеней, используя разложение на множители, графический способ
|
ФО [1], стр.58 ?
ИРД
СР[3], С-11
|
задачи с параметром
|
|
|
50-53
|
Уравнения, приводимые к квадратным.
|
4
|
КУ УПЗУ
УОНМ УОСЗ
|
квадратные уравнения, замена переменной, биквадратное уравнение
|
-уметь проводить замену переменной;
-уметь решать квадратные уравнения и уравнения, получившиеся из замены;
-знать и уметь решать биквадратные уравнения
|
ФО [1], стр.61 ?
ИРК,
ИРД
СР[3], С-13
|
|
|
|
54-56
|
Графический способ решения систем уравнений.
|
3
|
КУ УПЗУ УОНМ
|
график функции, системы уравнений, графический способ решения систем
|
-знать виды графиков и уметь их строить;
-уметь определять количество решений системы по графику;
-уметь решать системы графически
|
ФО [1], стр.66 ?
ИРД
СР [3], С-14
|
УМК Живая математика
|
|
|
57-60
|
Решение систем уравнений второй степени.
|
4
|
КУ УПЗУ УОНМ УОСЗ
|
системы уравнений второй степени, способы решения
|
-знать алгоритм решения систем второй степени;
-уметь их решать, используя известные способы (способ подстановки и способ сложения)
|
ФО [1], стр.68 ?
ИРД,
ИРК,
ПР [3], С-15
|
|
|
|
61-66
|
Решение задач с помощью систем уравнений второй степени.
|
6
|
КУ УПЗУ
|
алгоритм решения задач с помощью систем уравнений, способы решения
|
-уметь составлять причинно-следственные связи между данными в задаче и составлении уравнений, используя формулы;
-уметь решать системы уравнений различными способами
|
ФО [1], стр.72 ?
ИРД
СР [3], С-16
|
УМК Живая математика
|
|
|
67
|
Контрольная работа №5.
|
1
|
|
|
-уметь решать квадратные уравнения;
-уметь решать уравнения третьей и более степеней с помощью разложения на множители и введения вспомогательной переменной;
-уметь решать простейшие системы, содержащие одно уравнение первой, а другое второй степени;
-уметь решать текстовые задачи методом составления систем
|
[3], КР-2
|
|
|
|
IV
|
Соотношение между сторонами и углами треугольника
|
|
18
|
|
|
|
|
|
|
|
68-69
|
|
Синус, косинус, тангенс угла.
|
2
|
КУ
УОНМ УЗИМ
|
единичная полуокружность, основное тригонометрическое тождество, формулы приведения
|
-знать определение основных тригонометрических функций и их свойства;
-уметь решать задачи на применение формулы для вычисления координат точки
|
ФО [1], стр.271 ? 1-6
ИРД
СР[2], С-4
|
CD Математика 5-11/ Виртуальная лаборатория «Тригонометрические функции».
|
|
|
70
|
Площадь треугольника.
|
1
|
УОНМ
|
теорема о площади треугольника, формула площади
|
-уметь выводить формулу площади треугольника;
-уметь применять формулу при решении задач
|
ФО [1], стр.271 ? 7
ИРД
|
|
|
|
71
|
Теорема синусов.
|
1
|
УОСЗ
|
теорема синусов
|
-знать теорему синусов и уметь решать задачи на её применение
|
ФО [1], стр.271 ? 8
ИРД
|
CD Математика 5-11/ Виртуальная лаборатория «Тригонометрические функции».
|
|
|
72
|
Теорема косинусов.
|
1
|
КУ
|
теорема косинусов
|
-знать вывод формулы;
-уметь применять формулу при решении задач
|
ФО [1], стр.271 ? 9
ИРД
СР[2], С-5
|
обобщенная теорема Пифагора
|
|
|
73-77
|
Решение треугольников.
|
5
|
КУ УЗИМ
УОНМ УПЗУ
|
теорема синусов, теорема косинусов
|
-уметь находить все шесть элементов треугольника по каким-нибудь трем данным элементам, определяющим треугольник
|
ФО [1], стр.217 ? 10
ИРД
ИРК
СР[2], С-6
|
УМК Живая математика, задачи на решение треугольника
|
|
|
78
|
Контрольная работа №6.
|
1
|
|
|
-уметь применять теорему синусов и теорему косинусов в комплексе при решении задач
|
[3], КР-3
|
|
|
|
79
|
Угол между векторами
|
1
|
УОНМ
|
понятие угла между векторами
|
-знать, что такое угол между векторами
-уметь изображать угол между векторами
|
ФО [1]
|
|
|
|
80
|
Скалярное произведение векторов
|
1
|
УОНМ
|
понятие скалярного произведения векторов и его свойств, скалярный квадрат вектора
|
-знать определение скалярного произведения векторов, условие перпендикулярности ненулевых векторов.
-уметь вычислять скалярное произведение
|
ФО [1]
|
CD ИМ/Виртуальная лаборатория «Координатная плоскость».
|
|
|
81-82
|
|
Скалярное произведение в координатах. Свойства скалярного произведения векторов.
|
2
|
КУ
|
координаты вектора., свойства произведения, длина вектора
|
-знать теорему о скалярном произведении двух векторов и ее следствия
-уметь доказывать теорему, находить углы между векторами, используя формулу скалярного произведения в координатах
|
СР[2], С-12
|
CD ИМ/Виртуальная лаборатория «Координатная плоскость».
|
|
|
83-84
85
|
|
Решение задач по теме
Контрольная работа №7.
|
2
1
|
УПЗУ УОСЗ
|
теорема синусов, теорема косинусов, скалярное произведение векторов
|
-знать определение скалярного произведения и формулу в координатах.
-уметь решать простейшие планиметрические задачи
-уметь решать геометрические задачи с использованием тригонометрии
|
Проверка задач самостоятельного решения
[3], КР-4
|
|
|
|
|
|
V
|
Прогрессии
|
|
19
|
|
|
|
|
|
|
|
86-87
|
Последовательности.
|
2
|
КУ
УОНМ
|
последовательность, члены последовательности, формулы n-го члена последовательности, рекуррентные формулы
|
-приводить примеры последовательностей;
-уметь определять член последовательности по формуле
|
ФО [1], стр.81 ?
ИРД,
МД [2], Д-6.1
|
|
|
|
88-91
|
Арифметическая прогрессия. Формула n-го члена арифметической прогрессии.
|
4
|
КУ
УОСЗ
|
арифметическая прогрессия, разность, формула n-го члена арифметической прогрессии:
|
-уметь определять вид прогрессии по её определению;
-знать и применять при решении задач указанную формулу
|
ФО [1], стр.85 ?
ИРД
ПР [3], С-18
|
|
|
|
92-94
|
Формула суммы n первых членов арифметической прогрессии.
|
3
|
КУ
УОНМ УПЗУ
|
арифметическая прогрессия, формула суммы членов арифметической прогрессии:
|
-уметь находить сумму арифметической прогрессии по формуле
|
ФО [1], стр.90 ?
СР [3], С-19
|
|
|
|
95
|
Контрольная работа №8.
|
1
|
|
|
-уметь находить нужный член арифметической прогрессии;
-пользоваться формулой суммы членов арифметической прогрессии;
-определять является ли данное число членом арифметической прогрессии
|
[3], КР-3
|
|
|
|
96-99
|
Геометрическая прогрессия. Формула n-го члена геометрической прогрессии.
|
4
|
КУ УЗИМ
УПЗУ
|
геометрическая прогрессия, знаменатель геометрической прогрессии, формула n-го члена геометрической прогрессии:
|
-знать определение геометрической прогрессии;
-уметь распознавать геометрическую прогрессию;
-знать данную формулу и уметь использовать ее при решении задач
|
ФО [1], стр.93 ?
СР [3], С-20
ИРД
МД [2],
Д-6.2
|
|
|
|
100-103
|
Формула суммы n первых членов геометрической прогрессии.
|
4
|
КУ УЗИМ
|
геометрическая прогрессия, формула суммы членов геометрической прогрессии:
|
-знать и уметь находить сумму геометрической прогрессии по формуле
|
ФО [1], стр.98 ?
ИРД
СР [3], С-21
|
сумма бесконечной геометрической прогрессии
|
|
|
104
|
Контрольная работа №9
|
1
|
|
|
-уметь находить нужный член геометрической прогрессии;
-пользоваться формулой суммы n членов геометрической прогрессии;
-представлять в виде обыкновенной дроби бесконечную десятичную дробь
|
[3], КР-4
|
|
|
|
V1
|
Длина окружности и площадь круга
|
|
11
|
|
|
|
|
|
|
|
105-107
|
Правильные многоугольники.
|
3
|
КУ
УОСЗ
|
правильный многоугольник, вписанная и описанная окружность
|
-уметь вычислять угол правильного многоугольника по формуле;
-уметь вписывать окружность в правильный многоугольник и описывать
|
ФО [1], стр.290? 1-4
ИРД
ИРК
|
CD Математика 5-11/ Виртуальная лаборатория «Планиметрия».
|
|
|
108-111
|
Нахождение сторон правильного многоугольника через радиусы описанной и вписанной окружностей.
|
4
|
КУ УПЗУ УОНМ
УЗИМ УПКЗУ
|
площадь правильного многоугольника, его сторона, периметр, радиусы вписанной и описанной окружностей
|
-уметь решать задачи на применение формул зависимости между R, r, an;
-уметь строить правильные многоугольники
|
ФО [1], стр.290?5-7
ИРД
СР[2], С-7
|
УМК Живая математика, задачи на построение
|
|
|
112-114
|
Длина окружности и площадь круга.
|
3
|
КУ УПЗУ УОСЗ
|
длина окружности, площадь круга, площадь кругового сектора
|
-знать формулы для вычисления длины окружности и площади круга;
-уметь выводить формулы и решать задачи на их применение
|
ФО [1], стр.290? 8-12
ИРД
СР[2], С-8
|
УМК Живая математика
|
|
|
115
|
Контрольная работа №10.
|
1
|
|
|
-уметь решать задачи на зависимости между R, r, an;
-уметь решать задачи, используя формулы длины окружность, площади круга и кругового сектора
|
[3], КР-4
|
|
|
|
V11
|
Степень с рациональным показателем
|
|
17
|
|
|
|
|
|
|
|
116-118
|
Четные и нечетные функции.
|
3
|
КУ
|
четные и нечетные функции, их симметричность
|
-уметь по формуле определять четность и нечетность функции;
-приводить примеры этих функций;
-знать как расположен график четной и нечетной функции
|
ФО [1], стр.111 ?
ИРД
|
|
|
|
119-120
|
Функция 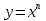 . .
|
2
|
УОНМ
|
степенная функция с натуральным показателем, свойства степенной функции и особенности ее графика при любом натуральном n
|
-знать свойства функции при n-четном и n-нечетном;
-уметь преобразовывать графики 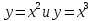 с наиболее высокими степенями с наиболее высокими степенями
|
ФО [1], стр.115 ?
ИРД
|
УМК Живая математика
|
|
|
121-123
|
Определение корня
n-й степени.
|
3
|
КУ
|
корень n-й степени, показатель корня, подкоренное выражение, арифметический корень
|
-знать таблицу степеней;
-уметь уметь вычислять значения некоторых корней n-ой степени
|
ФО [1], стр.120 ?
ИРД
|
|
|
|
124-127
|
Свойства арифметического корня n-й степени.
|
4
|
КУ
УПЗУ УОСЗ УОНМ
|
арифметический корень n-й степени, его свойства
|
-уметь применять свойства корня n-й степени при выполнении вычислений и преобразований
|
ФО [1], стр.124 ?
ИРД
СР [3], С-27
|
УМК Живая математика
|
|
|
128-131
|
Определение степени с дробным показателем.
|
4
|
КУ
|
степень с рациональным показателем и ее свойства
|
-уметь применять определение 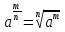 и наоборот и наоборот
|
ФО [1], стр.130 ?
ИРД
ПР [3], С-31
|
|
|
|
132
|
Контрольная работа №11
|
1
|
|
|
|
|
|
|
|
V111
|
Движения
|
|
8
|
|
|
|
|
|
|
|
133
|
Понятие движения.
|
1
|
УОНМ
|
отображение плоскости на себя
|
-знать , что является движением плоскости
|
ФО [1],
стр.303?1
ИРД
|
УМК Живая математика
|
|
|
134-135
|
Симметрия.
|
2
|
КУ УПЗУ
|
осевая и центральная симметрия
|
-знать какое отображение на плоскости является осевой симметрией, а какое центральной
|
ФО [1], стр.303 ?2-13
СР[2], С-9
|
УМК Живая математика
|
|
|
136-137
|
Параллельный перенос.
|
2
|
КУ УПЗУ УОНМ
УОСЗ
|
параллельный перенос
|
-знать свойства параллельного переноса;
-уметь строить фигуры при параллельном переносе на вектор  . .
|
ФО [1], стр.303 ?14,15
ИРД
|
УМК Живая математика
|
|
|
138-139
|
Поворот.
|
2
|
КУ УОСЗ
УПКЗУ
УЗИМ
|
поворот
|
-уметь строить фигуры при повороте на угол 
|
ФО [1], стр.303?16,17
ИРД
СР[2], С-10
|
УМК Живая математика
|
|
|
140
|
Контрольная работа №12.
|
1
|
|
|
-уметь строить фигуры при параллельном переносе и повороте
|
[3], КР-5
|
УМК Живая математика
|
|
|
1Х
|
Тригонометрические выражения и их преобразования
|
|
13
|
|
|
|
|
|
|
|
141-143
|
Определение синуса, косинуса, тангенса и котангенса.
|
3
|
КУ
УОНМ
|
начальный радиус, синус, косинус, тангенс и котангенс любого угла
|
-знать таблицу значений тригонометрических функций;
-уметь приводить углы поворота к виду
|
ФО [1], стр.152 ?
ИРД
|
|
|
|
144-146
|
Свойства тригонометрических функций.
|
3
|
УОСЗ
|
знаки синуса, косинуса, тангенса и котангенса, свойства тригонометрических функций
|
-определять знак выражения;
-упрощать выражения с применением формулы , четности и знака функции
|
ФО [1], стр.160 ?
|
УМК Живая математика
|
|
|
147-148
|
Радианная мера угла.
|
2
|
УПЗУ УОНМ
|
радиан, , радианная таблица значений тригонометрических функций
|
-осуществлять переход от радианной меры к градусной и от градусной меры к радианной
|
ФО [1], стр.162 ?
ИРД
СР [3], С-34
|
|
|
|
149-152
|
Соотношения между тригонометрическими функциями одного и того же угла.
|
4
|
КУ УПЗУ УОНМ УОСЗ
|
основные тригонометрические тождества и следствия из них
|
-уметь находить значение функции по одному известному, зная одну из функций;
-применять тождества при несложных тригонометрических преобразованиях
|
ФО[1],
стр. 168 ?
ИРД
ИРК
СР [3], С-40
|
|
|
|
|
|
153
|
Контрольная работа №13
|
1
|
|
|
-знать таблицу значений тригонометрических функций, формулы приведения;
-уметь выполнять несложные преобразования тригонометрических выражений;
|
[3], КР-5
|
|
|
|
Х
|
Элементы статистики и теории вероятностей
|
|
8
|
|
|
|
|
|
|
|
154
|
Примеры комбинаторных задач.
|
1
|
КУ
|
перебор возможных вариантов, комбинаторное правило умножения
|
-ориентироваться в комбинаторике;
-уметь строить дерево возможных вариантов
|
ФО[8], стр.37?
|
|
|
|
155-157
|
Перестановки, размещения, сочетания.
|
3
|
КУ
|
перестановки, число всевозможных перестановок, размещения, сочетания
|
-знать и уметь пользоваться формулами для решения комбинаторных задач
|
ФО[8], стр.41?
|
|
|
|
158
|
Вероятность случайного события.
|
1
|
КУ
|
случайное событие, относительная частота, классическое определение вероятности
|
-определять количество равновозможных исходов некоторого испытания;
-знать классическое определение вероятности
|
ФО[8], стр.51?
|
|
|
|
159-160
|
Сложение и умножение вероятностей.
|
2
|
КУ
|
противоположные события, независимые события, несовместные и совместные события
|
-знать формулу вычисления вероятности в случае исхода противоположных событий
|
ФО[8], стр.60?
|
|
|
|
161
|
Обобщающий урок.
|
1
|
КУ
|
элементы комбинаторики
|
-уметь применять все знания в комплексе
|
ФО[8]
|
|
|
|
|
Итоговое повторение курса геометрии 8 класса
|
|
13
|
|
|
|
|
|
|
|
162-163
|
Об аксиомах планиметрии.
|
2
|
КУ
УПКЗУ
|
аксиомы планиметрии
|
-знать все об аксиомах планиметрии
|
ФО [1],
ИРД
|
|
|
|
164-168
|
Решение задач в координатах.
|
5
|
КУ УОСЗ
|
координаты вектора, метод координат
|
-уметь находить координаты вектора через координаты его начала и конца;
- уметь вычислять длину вектора по его координатам, координаты середины отрезка и расстояние между двумя точками
|
ФО [1],
ИРД
ИРК
|
УМК Живая математика
|
|
|
169-174
|
Теоремы синусов и косинусов.
|
6
|
КУ УПЗУ
|
теорема синусов, теорема косинусов
|
- уметь находить все элементы треугольника по каким-нибудь трем данным элементам, определяющим треугольник
|
ФО [1],
ИРД
|
|
|
|
|
Итоговое повторение курса алгебры 9 класса
|
|
24
|
|
|
|
|
|
|
|
175-180
|
Графики функций.
|
6
|
КУ УПЗУ
|
область определения и область значений функций
|
-знать алгоритм построения графика функции;
-уметь строить графики функции;
-уметь по графику определять свойства функции
|
ФО
ИРД
|
|
|
|
181-187
|
Уравнения, неравенства, системы.
|
7
|
КУ УПЗУ
|
квадратные уравнения, неравенства второй степени, системы уравнений
|
-уметь решать уравнения третьей и четвертой степени с одним неизвестным с помощью разложения на множители и введения вспомогательной переменной;
-уметь решать неравенства методом интервалов;
-уметь решать системы уравнений
|
ФО
ИРД
|
|
|
|
188-194
|
Текстовые задачи.
|
7
|
КУ
УПЗУ
|
решение текстовых задач
|
-уметь решать задачи с помощью составления систем
|
ФО
ИРД
|
|
|
|
195-201
|
|
Арифметическая и геометрическая прогрессии.
|
7
|
КУ УПКЗУ
|
разность арифметической прогрессии, знаменатель геометрической прогрессии, сумма n-го члена арифметической и геометрической прогрессии
|
-знать формулы n-го члена и суммы n членов арифметической и геометрической прогрессий и уметь их применять при решении задач
|
ФО
ИРД
|
|
|
|
202-205
|
Итоговая административная контрольная работа.
|
4
|
|
|
-уметь применять все полученные знания за курс алгебры 9 класса
|
|
|
|
|
Уроки №206-210 резервные
|
Уроки №68,69, 70 резервные
|
Литература:
Артюнян Е. Б., Волович М. Б., Глазков Ю. А., Левитас Г. Г. Математические диктанты для 5-9 классов. – М.: Просвещение, 1991.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия 7-9. – М.: Просвещение, 2007.
Буланова Л. М., Дудницын Ю. П. Проверочные задания по математике для учащихся 5-8 и 10 классов. – М.: Просвещение, 1998.
Жохов В. И., Макарычкв Ю. Н., Миндюк Н. Г. Дидактические материалы по алгебре, 9 класс. – М.: Просвещение, 2002.
Звавис А. И., Шляпочкин Л. Я. Контрольные и проверочные по алгебре 7-9 классы. М.: Просвещение, 2003.
Зив Б. Г., Мейлер В. М. Дидактические материалы по геометрии за 9 класс. – М.: Просвещение, 2005.
Иченская М. А. Самостоятельные и контрольные работы к учебнику Л. С. Атанасяна 7-9 классы. – Волгоград: Учитель, 2006.
Колягин Ю. М., Сидоров Ю. В. Изучение алгебры в 7-9 классах. –М.: Просвещение, 2002.
Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Алгебра 9. – М.: Просвещение, 2007.
Макарычкв Ю. Н., Миндюк Н. Г. Элементы статистики и теории вероятностей, алгебра 7-9 классы. – М.: Просвещение, 2007.
Миндюк Н. Г. Разноуровневые дидактические материалы по алгебре, 9 класс. – М.: Просвещение, 2006.
Электронные учебные пособия
Интерактивная математика. 5-9 класс. Электронное учебное пособие для основной школы. М., ООО «Дрофа», ООО «ДОС»,, 2002.
Математика. Практикум. 5-11 классы. Электронное учебное издание. М., ООО «Дрофа», ООО «ДОС», 2003.
|
|
|
 Скачать 464.54 Kb.
Скачать 464.54 Kb.
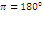
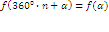
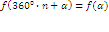
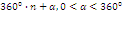
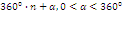
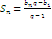
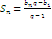
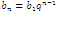
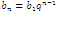
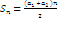
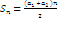
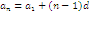
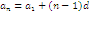 Кочурова Екатерина Игоревна учитель МКОУ СОШ села Синегорье Нагорского района Кировской области.
Кочурова Екатерина Игоревна учитель МКОУ СОШ села Синегорье Нагорского района Кировской области.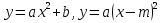 . Формируются умения решать неравенства вида:
. Формируются умения решать неравенства вида: 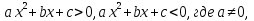 которые опираются на сведения о графике квадратичной функции. На этапе 9-го класса завершается изучение рациональных уравнений с одной переменной. Дается понятие целого рационального уравнения и его степени. Особое внимание уделяется решению уравнений третьей и четвертой степени с помощью разложения на множители и введения вспомогательной переменной, что широко используется в дальнейшем при решении тригонометрических, логарифмических и других видов уравнений. Рассматриваются системы, содержащие уравнения второй степени с двумя неизвестными. Даются первые знания об арифметической и геометрической прогрессиях, как о частных видах последовательностей. Изучая формулу нахождения суммы
которые опираются на сведения о графике квадратичной функции. На этапе 9-го класса завершается изучение рациональных уравнений с одной переменной. Дается понятие целого рационального уравнения и его степени. Особое внимание уделяется решению уравнений третьей и четвертой степени с помощью разложения на множители и введения вспомогательной переменной, что широко используется в дальнейшем при решении тригонометрических, логарифмических и других видов уравнений. Рассматриваются системы, содержащие уравнения второй степени с двумя неизвестными. Даются первые знания об арифметической и геометрической прогрессиях, как о частных видах последовательностей. Изучая формулу нахождения суммы 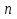 первых членов арифметической прогрессии
первых членов арифметической прогрессии 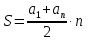 и формулу суммы
и формулу суммы 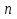 первых членов геометрической прогрессии
первых членов геометрической прогрессии 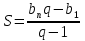 , целесообразно уделить внимание заданиям, связанным с непосредственным применением этих формул. Из курса геометрии продолжается изучение синуса, косинуса и тангенса острого угла прямоугольного треугольника. Вводится понятие котангенса угла. Изучаются свойства синуса, косинуса, тангенса и котангенса, которые находят применение в преобразованиях тригонометрических выражений. Специальное внимание уделяется переходу от радианной меры угла к градусной мере и наоборот. Центральное место занимают формулы, выражающие соотношения между тригонометрическими функциями одного и того же аргумента. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
, целесообразно уделить внимание заданиям, связанным с непосредственным применением этих формул. Из курса геометрии продолжается изучение синуса, косинуса и тангенса острого угла прямоугольного треугольника. Вводится понятие котангенса угла. Изучаются свойства синуса, косинуса, тангенса и котангенса, которые находят применение в преобразованиях тригонометрических выражений. Специальное внимание уделяется переходу от радианной меры угла к градусной мере и наоборот. Центральное место занимают формулы, выражающие соотношения между тригонометрическими функциями одного и того же аргумента. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.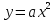 .
.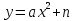 и
и 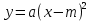 .
.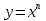 .
.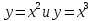 с наиболее высокими степенями
с наиболее высокими степенями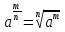 и наоборот
и наоборот .
.