Протокол № от 2013 г. «Согласовано» Заместитель директора школы по увр мкоу «Синелипяговская сош»
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
Место предмета в базисном учебном плане:согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения математики на этапе основного общего образования отводится не менее 210 ч. из расчета 6 ч в неделю.
В результате изучения алгебры и начал анализа на профильном уровне в старшей школе ученик должен Знать/понимать
Уметь:
В результате изучения геометрии на профильном уровне в старшей школе ученик должен Уметь:
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
5. Содержание программы учебного курса. 1. Действительные числа Понятие натурального числа. Множества чисел. Свойства действительных чисел. Метод математической индукции. Перестановки. Размещения. Сочетания. Доказательство числовых неравенств. Делимость целых чисел. Сравнение по модулю т. Задачи с целочисленными неизвестными. Основная цель: Систематизировать известные и изучить новые сведения о действительных числах. 2. Рациональные уравнения и неравенства Рациональные выражения. Формулы бинома Ньютона, суммы и разности степеней. Рациональные уравнения. Системы рациональных уравнений. Метод интервалов решения неравенств. Рациональные неравенства. Системы рациональных неравенств. Основная цель: Сформировать умения решать рациональные уравнения и неравенства. 3. Некоторые сведения из планиметрии. Углы и отрезки, связанные с окружностью. Решение треугольников. Теоремы Менелая и Чевы. Эллипс, гипербола и парабола. 4. Введение. Предмет стереометрии. Аксиомы стереометрии. Некоторые следствия из аксиом. Основная цель – познакомить учащихся с содержанием курса стереометрии, с основными понятиями и аксиомами, первые следствия из аксиом. 5. Параллельность прямых. Параллельность прямых, прямой и плоскости. Взаимное расположение двух прямых в пространстве. Угол между двумя прямыми. Основная цель – сформировать представления учащихся о возможных случаях взаимного расположения прямых в пространстве, прямой и плоскости. 6. Корень степени п Понятие функции и ее графика. Функция у = х 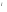 . Понятие корня степени п. Корни четной и нечетной степеней. Арифметический корень. Свойства коней степени п. Функция y = . Понятие корня степени п. Корни четной и нечетной степеней. Арифметический корень. Свойства коней степени п. Функция y = Основная цель - Освоить понятия коня степени п и арифметического корня; выработать умение преобразовывать выражения, содержащие корни степени п. 7. Степень положительного числа Понятие и свойства степени с рациональным показателем. Предел последовательности. Свойства пределов. Бесконечно убывающая геометрическая прогрессия. Число е. Понятие степени с иррациональным показателем. Показательная функция. Основная цель - Усвоить понятия рациональной и иррациональной степеней положительного числа и показательной функции. 8. Параллельность плоскостей. Параллельность плоскостей. Тетраэдр и параллелепипед. Основная цель – Изучить свойства и признаки параллельности прямых и плоскостей. 9. Логарифмы Понятие и свойства логарифмов. Логарифмическая функция Основная цель: Освоить понятие логарифма и логарифмической функции, выработать умение преобразовывать выражения, содержащие логарифмы. 10. Показательные и логарифмические уравнения и неравенства Простейшие логарифмические уравнения и неравенства. Уравнения и неравенства, сводящиеся к простейшим заменой неизвестного. Основная цель: Сформировать умение решать показательные и логарифмические уравнения и неравенства. 11. Перпендикулярность прямых и плоскостей. Перпендикулярность прямой и плоскости. Перпендикуляр и наклонные. Угол между прямой и плоскостью. Двугранный угол. Перпендикулярность плоскостей. Трехгранный, многогранный угол. Основная цель – ввести понятие перпендикулярности прямых и плоскостей, изучить признаки перпендикулярности прямой и плоскости, двух плоскостей; расстояние от точки до плоскости, расстояние между двумя параллельными плоскостями, между скрещивающимися прямыми. 12. Синус и косинус угла Понятие угла и его меры. Определение синуса и косинуса угла, основные формулы для них. Арксинус и арккосинус. Основная цель: Освоить понятия синуса и косинуса произвольного угла, изучить свойства функций угла: sin 13. Тангенс и котангенс угла Определения тангенса и котангенса угла и основные формулы для них. Арктангенс и арккотангенс. Основная цель: Освоить понятия тангенса и котангенса произвольного угла, изучить свойства функций угла: tg 14. Формулы сложения Косинус суммы и разности двух углов. Формулы для дополнительных углов. Синус суммы и разности двух углов. Сумма и разность синусов и косинусов. Формулы для двойных и половинных углов. Произведение синусов и косинусов. Формулы для тангенсов. Основная цель: Освоить формулы синуса и косинуса суммы и разности двух углов, выработать умения выполнять тождественные преобразования тригонометрических выражений с использованием выведенных формул. 15. Тригонометрические функции числового аргумента Функции y = sin x, y = cos x, y = tg x, y = ctg x. Основная цель: Изучить свойства основных тригонометрических функций и их графиков. 16. Многогранники Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера. Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрий в окружающем мире. Сечения куба, призмы, пирамиды. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр). Основная цель: познакомить учащихся с основными видами многогранников (призма, пирамида, усечённая пирамида), с правильными многогранниками и элементами их симметрии. 17. Тригонометрические уравнения и неравенства Простейшие тригонометрические уравнения. Тригонометрические уравнения, сводящиеся к простейшим заменой неизвестного. Применение основных тригонометрических формул для решения уравнений. Однородные уравнения. Простейшие тригонометрические неравенства. Неравенства, сводящиеся к простейшим заменой неизвестного введение вспомогательного угла. Основная цель: Сформировать умения решать тригонометрические уравнения и неравенства. 18. Вероятность события Понятия и свойства вероятности события. Основная цель: Овладеть классическим понятием вероятности события, изучить его свойства и научиться применять их к при решении задач. 19. Частота. Условная вероятность Относительная частота события. Условная вероятность. Независимые события. Основная цель: Овладеть понятиями частоты события и условной вероятности события, независимых событий; научить применять их при решении задач. 20. Повторение Перечень контрольных работ 1. Контрольная работа № 1по теме «Рациональные уравнения и неравенства» 2. Контрольная работа №2 по теме «Взаимное расположение прямых в пространстве. Угол между двумя прямыми». 3. Контрольная работа № 3 по теме: «Корень степени n» 4. Контрольная работа № 4 «Степень положительного числа». 5. Контрольная работа № 5 по теме «Параллельность плоскостей. Тетраэдр. Параллелепипед » 6. Контрольная работа № 6: «Показательные и логарифмические уравнения и неравенства» 7. Контрольная работа № 7 по теме «Перпендикулярность прямых и плоскостей» 8. Контрольная работа № 8 по теме: «Синус, косинус, тангенс и котангенс угла» 9. Контрольная работа № 9 по теме: «Формулы сложения. Тригонометрические функции числового аргумента». 10. Контрольная работа № 10 по теме «Многогранники» 11. Контрольная работа № 11по теме: « «Тригонометрические уравнения и неравенства». 12. Итоговая контрольная работа № 12
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||