Программа По теме «Обратные тригонометрические функции»
 Скачать 107.94 Kb. Скачать 107.94 Kb.
|
| Урок алгебры и начала анализа Класс 10 Муниципальное общеобразовательное учреждение – лицей г. Алейска Алтайского края Направление физико-математическое Учитель Маркова Людмила Константиновна В основу урока положена модульная педагогическая технология, главным отличием которой является планирование совместной деятельности ученика и учителя. Данный урок 7-8 в системе уроков по теме «Обратные тригонометрические функции» и 2-3 по теме «Упражнения, содержащие обратные тригонометрические функции». Модуль рассчитан на 2 часа. Принцип отбора содержания – постепенное увеличение трудности. В каждом учебном элементе даётся указание учителя, необходимый теоретический материал. Форма работы учащихся – индивидуальная, в начале урока – работа в парах. Основной метод – самостоятельная работа. Урок способствует формированию ОУУН таких, как планирование деятельности, умение выделить главное, сопоставлять, сравнивать, проводить аналогии, навыков самооценки и самоконтроля. Теоретическое планирование тем М1 М2 М3 М4 М5 М6 М7 1 2-3 4-5 6 7-8 9 10 М1 - Определение арксинуса, арккосинуса. М2 – Свойства и графики обратных тригонометрических функции. М3 – Преобразование и вычисление выражений, содержащих обратные тригонометрические функции (практикум). М4 - Способы решения уравнений, содержащих обратные тригонометрические функции (урок-лекция). М5 - Решение уравнении, содержащих обратные тригонометрические функции (урок-практикум). М6 — Решение простейших неравенств. содержащих обратные тригонометрические функции. М7 — контрольная работа Модульная программа По теме «Обратные тригонометрические функции» Комплексная дидактическая цель: - усвоить понятия «арксинус», «арккосинус», «арктангенс». «арккотангенс», научиться вычислить их значения; - изучить свойства обратных тригонометрических функций, научиться строить их графики; - уметь применять изученные свойства и определения обратных тригонометрических функций для преобразования и вычисления значений выражений, содержащих обратные тригонометрические функции; - изучить основные методы и приемы решения уравнений, содержащих обратные тригонометрические функции. Знать: 1. Определения обратных тригонометрических функций 2. Свойства и график каждой обратной тригонометрической функция y=arcsin х. y=arccos х. y=arctg x, y=arcctg x 3. Основные тождества, связанные с обратными тригонометрическими функциями. Уметь: 1. Находить значения обратных тригонометрических функции для «табличных» значений аргумента; 2. Применять определения и свойства обратных тригонометрических функция для преобразования и вычисления значений выражений, содержащих обратные тригонометрические функции. 3. Решать уравнения и неравенства, содержащие обратные тригонометрические функции Тема урока: Решение уравнений, содержащих обратные тригонометрические функции. Тип урока: урок формирования навыков и умений. Вид урока: урок – практикум. Цели урока: Образовательные: 1. Формировать умения решать уравнения, содержащие обратные тригонометрические функции, применяя определения и свойства этих функций. 2. Способствовать формирования общеучебных умений и навыков: самооценки и самоконтроля, планирования своей деятельности, умения выделить признаки объектов и на их основе проводить сравнения, аналогии. Развивающие: Способствует развитию:
Воспитательные: Способствовать:
- целеустремлённости через потребности ставить цели и достигать их; - настойчивости, воли через формирование способности к преодолению трудностей; 2. формированию: - осознанности своих действий; - положительной мотивации учения через создания ситуации успехов; Оборудование: модульная программа для каждого ученика, набор карточек с ключами для проверки решений учащимися Ход урока I Сообщение темы и постановка цели урока II Водный инструктаж учителя Сегодня вы будете работать с модульной программой, состоящей из 6 учебных элементов. Выполнив задания самостоятельной работы, вы должны объявить о её окончании и получить от учителя эталон. Свои ответы каждый из вас должен сравнить с эталонными и исправить ошибки. Если вы получили менее указанного в инструктаже баллов, то должны набрать дополнительные баллы в корректирующих заданиях. Для этого необходимо решить задания другого варианта, аналогичные тем, где допущена ошибка. При необходимости вы можете обратиться за консультацией к учителю. Оценка за весь модуль зависит от суммы набранных баллов по всем учебным элементам. Для оценки «5» необходимо набрать не менее 31 балла (из 34 возможных), если 25 <= n <> 30, то получите оценку «4», при 20<= n <> 24 – оценка «3», при <20 – оценка «2». Выполнив задание, каждый раз необходимо отмечать количество баллов в оценочном листе. III Работа с модульной программой IV Подведение итогов урока V Информация о домашнем задании Модульная программа урока УЭ – 0 – интегрирующая цель УЭ – 1 входной контроль УЭ – 2 простейшие уравнения, содержащие обратные тригонометрические функции УЭ – 3 уравнения, содержащие обратные тригонометрические функции, вида P(f(x))=0 УЭ – 4 уравнения, содержащие разные обратные тригонометрические функции, зависящие от разных аргументов УЭ – 5 выходной контроль УЭ – 6 самооценка и рефлексия. Оценочный лист учащихся
УЭО Интегрирующая цель. В процессе работы над учебными элементами вы должны: повторить определения и свойства обратных тригонометрических функций, научиться определять тип уравнения и применять изученные свойства функции и их определения для решения уравнения в соответствии с выбранным способом, научиться решать уравнения, содержащие обратные тригонометрические функции; определить свой уровень знаний по теме. Учебный элемент 1 (15мин) Цель: Повторить определения обратных функций и основные тождества, связанные с ними.
1 вариант 2 вариант Найдите значение выражения.
Список правильных ответов получите у учителя Исправьте ошибки и проставьте заработанных баллов в свой оценочный лист. Если вы набрали 6 баллов и выше, то переходите к следующему учебному элементу. Если же набрали меньше 6 баллов, то прорешайте задания из другого варианта, аналогичные тем, в которых была допущена ошибка, и проставьте набранные баллы в графу и «корректирующие задания». Учебный элемент 2 (12мин) Цель: Закрепить умения решить простейшие уравнения, содержащие обратные тригонометрические функции.
Используя приведённую выше таблицу и свойства обратных тригонометрических функций, решить уравнения, содержащие обратные тригонометрические функции Пример: arccos x – arcsin x = arccos √3/2. Решение: Учитывая, что arccos √3/2 = π/6 и arcsin x + arccos x = π/2, заменим в уравнении arcsin x выражением π/2 – arccos x, получим уравнение arccos x – (π/2 – arccos x)= π/6, 2arccos x - π/2 = π/6, 2arccos x = 2π/3. arccos x = π/3, x = cos π/3, x= ½ Ответ: ½ Задания самостоятельной работы: 1 вариант 2 вариант
Проверьте и оцените свою работу. Правильные ответы возьмите у учителя. Если есть ошибки, исправьте их, проставьте количество балов в оценочные листы. Если вы набрали 5 и более балов, то переходите к следующему учебному элементу, если же меньше 5, то решайте задания другого варианта, аналогично тому, в котором сделали ошибку. Проставьте набранные баллы в графу «корректирующие задания». Учебный элемент 3 (13мин) Цель: Формировать умение решать уравнения, содержащие обратные тригонометрические функции, вида P(f(x)) = 0, где P – некоторая рациональная функция, а f(x) – одна из аркфункций.
Пример. 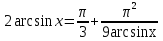 Решение. Пусть 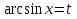 , где , где 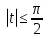 Уравнение имеет вид 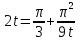 Оно равносильно системе 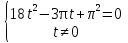 Решим квадратное уравнение: 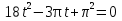 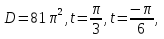 Оба корня отличны от нуля и удовлетворяют условиям 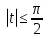 Решим совокупность уравнений: 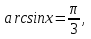 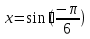 , , 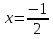 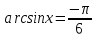 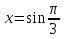 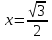 Ответ: 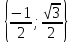 . .
Задания самостоятельной работы 1 вариант 2 вариант
Проверьте и оцените свою работу. Если вы получили 5 баллов, переходите к следующему учебному элементу, если есть ошибки – исправьте их и решите задания другого варианта, аналогичные тому, в которых допущены ошибки. Поставьте количество баллов в оценочный лист. Учебный элемент 4 (15 мин) Цель: Формировать умения решать уравнения, содержащие разные обратные тригонометрические функции или функции, зависящие от разных аргументов.
Если в уравнения входят выражения, содержащие разные обратные функции или они зависят от разных аргументов, то сведение уравнения к его алгебраическому следствию осуществляется обычно вычислением некоторой тригонометрической функции от обеих частей уравнения. Получившиеся при этом посторонние корни определяются проверкой. Если в качестве прямой функции выбирается тангенс или котангенс, то решение, не входящее в область определения этих функций, могут быть потеряны. Поэтому перед вычислением значений тангенса или котангенса от обеих частей уравнения, следует убедиться в том, что среди чисел , не входящих в область определения этих функций, нет корней исходного уравнения. Пример: Решить уравнение 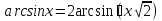 Решение: Если равны углы, то равны и тригонометрические функции от них (обратное неверно). 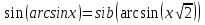 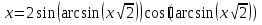 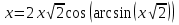 Найдем 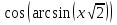 Пусть 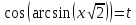 . Тогда sin t= . Тогда sin t=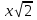 , , 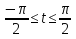 (по определению арксинуса) (по определению арксинуса)cos t= 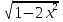 Получим уравнение 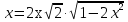 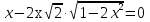 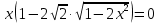 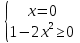 или или 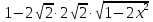 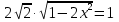 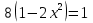 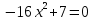 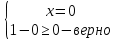 х2= х2= 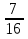 ; х= ; х=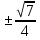 Проверка: при х=0 arcsin0=2arcsin0 0=0 – верно 0 – корень уравнения Если х= 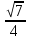 , 0 < arcsin , 0 < arcsin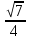 < < 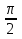 Найдем arcsin(x 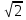 )=arcsin )=arcsin 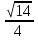 > arcsin > arcsin 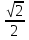 > > 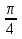 Следовательно, 2arcsin 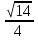 >2 >2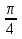 , 2arcsin , 2arcsin 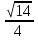 > > 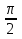 Итак, при х= 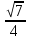 левая часть уравнения меньше левая часть уравнения меньше 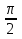 , а правая – больше , а правая – больше 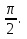 Значит, 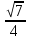 - посторонний корень. - посторонний корень.Если х=  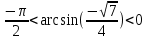 arcsin( 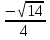 ) < arcsin( ) < arcsin(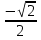 ) < ) < 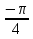 , ,arcsin( 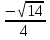 ) < ) < 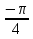 , 2arcsin , 2arcsin 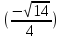 < < 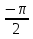 Левая часть уравнения больше, чем 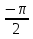 , а правая – меньше, чем , а правая – меньше, чем 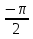 ; ;Значит,  – посторонний корень. – посторонний корень.Ответ: {0}.
Проверьте и оцените свою работу, показав ее учителю. Если есть ошибки – исправьте их. После этого переходите к следующему элементу. Учебный элемент 5 (20 мин) Цель: Проверить усвоение изученной темы. Выполните самостоятельную работу: 1 вариант 2 вариант
Проверьте и оцените свою работу, взяв ответы и решения у учителя. Исправьте ошибки, если они есть. Поставьте баллы в оценочные листы. Если допущены ошибки, то прорешайте аналогичные задания из другого варианта. Если ошибок нет, то переходите к следующему учебному элементу. Учебный элемент 6 (4 мин) Цель: самооценка и рефлексия. Подсчитайте все полученные баллы. Если вы набрали не менее 31 балла, то получаете «5» Если вы набрали от 25 до 30, то «4», если от 20 до 24 – «3». Ответьте на вопросы:
Домашнее задание (2 мин)
| ||||||||||||||||||||||||||||||||||||||||||||||