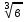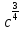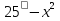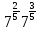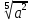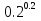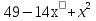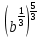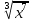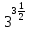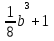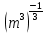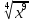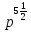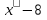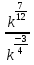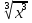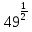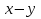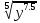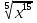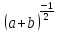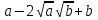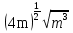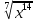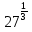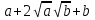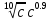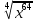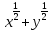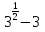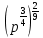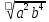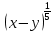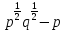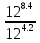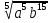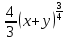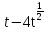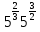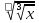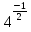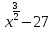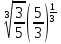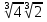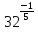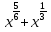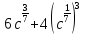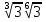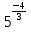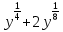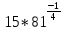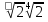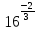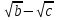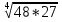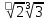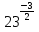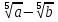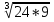Преобразование иррациональных выражений
 Скачать 56.67 Kb. Скачать 56.67 Kb.
|
| Методическая разработка урока в 11 классе для подготовки к ЕГЭ на тему: «Преобразование иррациональных выражений». Обобщающее повторение. Цели: -обобщить и систематизировать знания по теме «Преобразование иррациональных выражений» -учиться применять полученные знания в задачах ЕГЭ части В и как элемент задачи части С. Оборудование: раздаточные материалы, настенные таблицы. Ход урока.
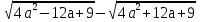 При a> 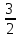
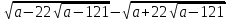 При условии, что a>242 f(x)= 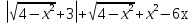 при решении этого упражнения находим область определения функции и упрощаем выражение, задающее функцию, остальное доделываем дома
Приложение №1 1 столбец. Представить в виде степени. 2 столбец. Представить в виде корня n-степени. 3 столбец. Разложить на множители. 4 столбец. Представить в виде степени.
ПРИЛОЖЕНИЕ №2. КАРТОЧКИ – ОШИБКИ. №1 Все числа равны между собой. Возьмём два произвольных не равных между собой числа a и b 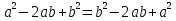 . .Слева и справа стоят полные квадраты, т.е. можем записать 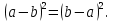 Извлекая из обеих частей равенства квадратный корень, получим a-b=b-a или 2a=2b, или окончательно a=b. №2 Половина любого числа равна половине ему противоположного. Возьмём произвольное число a и положим x=- 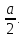 Тогда 2x+a=0 или после умножения на a получим 2ax + 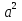 =0. =0. Прибавляя к обеим частям этого равенства 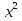 , имеем , имеем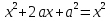 Так как 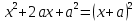 ,то предыдущее равенство можно записать в виде ,то предыдущее равенство можно записать в виде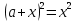 , ,а после извлечения квадратного корня из обеих частей последнего равенства получаем 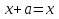 . . Поскольку по условию x=- 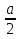 , то из равенства имеем , то из равенства имеем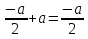 , и поэтому получаем окончательно , и поэтому получаем окончательно 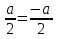 . .№3 Квадратный корень из отрицательного числа существует. Пусть a – произвольное положительное число, и положим x=-a. Тогда 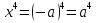 , а т.к. , а т.к. 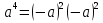 , то , то 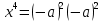 . .Извлекая из обеих частей равенства корень четвертой степени, получаем 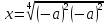 . . Но корень из произведения двух множителей равен произведению корней из этих множителей, т.е. 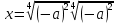 , ,что, в свою очередь, может быть представлено в виде x= 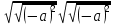 . . Последнее равенство можно записать так: x= 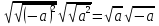 . .Возвращаясь к исходному случаю x=-a, получаем, что 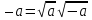 , а разделив обе части равенства на , а разделив обе части равенства на 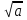 , получим , получим 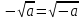 , т.е. квадратный корень из отрицательного числа (-a) и равен минус квадратному корню из числа a. , т.е. квадратный корень из отрицательного числа (-a) и равен минус квадратному корню из числа a.№4 Сумма любых двух одинаковых чисел равна нулю. Возьмем произвольное неравное нулю число a и напишем уравнение x=a. Умножая обе его части на (-4а), получим -4ах=-4 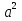 . Прибавляя к обеим частям этого равенства . Прибавляя к обеим частям этого равенства 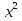 и перенеся член и перенеся член 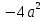 влево с противоположным знаком, получим влево с противоположным знаком, получим 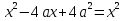 , ,откуда, замечая, что слева стоит полный квадрат, имеем 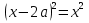 , ,или x-2a=x. Заменяя в последнем равенстве х на равное ему число а, получим а-2а=а, или –а=а, откуда 0=а+а, т.е. сумма двух произвольных одинаковых чисел а равна нулю. Приложение 3 Вариант 1 А1. Выполните действия: 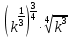 . .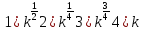 А2. Найдите значение выражения 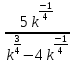 при k=5. при k=5.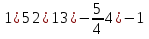 В1. Найдите значение выражения 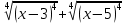 , если , если 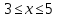 Вариант 2 А1. Упростите выражение: 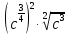 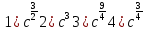 А2. Найдите значение выражения 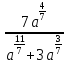 при а=2 при а=2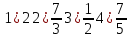 В1. Найдите значение выражения 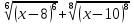 , если , если 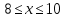 |