Пояснительная записка. При изучении тем «Четырехугольники»
 Скачать 84.21 Kb. Скачать 84.21 Kb.
|
| МАОУ «Средняя общеобразовательная школа № 26 с углубленным изучением химии и биологии» «Четырехугольники» Автор Келка Марина Леонидовна Учитель математики Великий Новгород 2012 г Пояснительная записка. При изучении тем «Четырехугольники» в 8 классе в работе использую общую основную схему описания многоугольника. Существует несколько способов получения алгоритма:
Третий способ является наиболее результативным, поскольку он позволяет развивать логическое мышление, заставляет ученика думать, а не получать готовый продукт деятельности учителя. Поэтому, опираясь на знания, полученными учащимися в начальной школе, данная схема получена при совместной работе учителя и ученика. Создание схемы помогает учащимся при дальнейшем изучении различных видов четырехугольников, основные пункты новой фигуры (общие для всех) они называют сами, а педагог помогает выяснить индивидуальные особенности изучаемого четырехугольника. При этом происходит формирование умений выделять главное, существенное в изучаемом материале, сравнивать, классифицировать, обобщать изучаемые факты и понятия. Материал направлен на развитие познавательных способностей, навыков самостоятельной работы. После введения алгоритма необходимо закрепление на многократном повторении действий, которое происходит как в ходе устной работы, так и при решении письменных задач. При устном проговаривании следует не только называть свойства фигур с помощью данных обозначений (сторона АВ, СD и пр.), но применять к этому фразы « противоположные стороны…, боковые стороны…, противоположные углы…. » , что приводит к умению обобщать и классифицировать изучаемые в факты. В основу данной работы положены учебные темы: «Виды четырехугольников их свойства, признаки», «Площади многоугольников». В дальнейшем материалы используются в 10 – 11 классе при изучении темы «Поверхность тел вращения», «Площадь поверхности» и др. Одно из важнейших свойств алгоритма – массовость, позволяет применять данную схему для целой группу геометрических фигур. Схема описания (общая).
- взаимное расположение противоположных сторон (параллельны/ не паралелльны); - взаимное расположение боковых сторон (перпендикулярны/ не перпендикулярны/ расположены под углом… ) - соотношение длин противоположных сторон (равны/ не равны); - соотношение длин боковых сторон (равны/ не равны); - соотношение длин всех сторон (равны/ не равны);
- соотношение величин противоположных углов ( равны/ не равны); - соотношение величин соседних углов ( равны/ не равны); - соотношение величин всех углов ( равны/ не равны);
- взаимное расположение диагоналей (перпендикулярны/ не перпендикулярны/ расположены под углом…); - соотношение длин диагоналей (или их частей) (равны/ не равны);
- сумма противоположных углов; - сумма соседних углов;
Параллелограмм. Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны, т.е. лежат на параллельных прямых. 
АB ║ CD (противоположные стороны) АB = CD (противоположные стороны) BC ║ АD (противоположные стороны) BC = АD (противоположные стороны)
∟A = ∟C (противоположные углы) ∟B = ∟D (противоположные углы)
О – точка пересечения диагоналей. АО = ОС ВО = ОD
∟A+∟B+∟C+ ∟D = (4 - 2) 1800 = 3600 ∟A+∟B = 1800 ∟B+∟C = 1800 ∟C+ ∟D = 1800 ∟A+∟D = 1800
a – основание h – высота Прямоугольник. Прямоугольник – четырёхугольник, у которого все углы прямые (равны 90 градусам). Прямоугольник является частным случаем параллелограмма 
АB ║ CD АB = CD BC ║ АD BC = АD AB ┴ AD CD ┴ AD AB ┴ BC CD ┴ BC
∟A = ∟C = ∟B = ∟D = 90◦
О – точка пересечения диагоналей. АО = ОС ВО = ОD
∟A+∟B+∟C+ ∟D = (4 - 2) 1800 = 3600 ∟A+∟B = 1800 ∟B+∟C = 1800 ∟C+ ∟D = 1800 ∟A+∟D = 1800
a, b - стороны Ромб. Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма 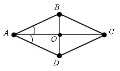
АB ║ CD АB = CD = BC = АD BC ║ АD
∟A = ∟C ∟B = ∟D
О – точка пересечения диагоналей. АО = ОС ВО = ОD AC ┴ BD
∟A+∟B+∟C+ ∟D = (4 - 2) 1800 = 3600 ∟A+∟B = 1800 ∟B+∟C = 1800 ∟C+ ∟D = 1800 ∟A+∟D = 1800
a – сторона h - высота Квадрат. Квадрат – правильный четырёхугольник, у которого все стороны и углы равны между собой. Квадрат является частным случаем прямоугольника, ромба и параллелограмма. 
АB ║ CD АB = CD = BC = АD BC ║ АD AB ┴ AD CD ┴ AD AB ┴ BC CD ┴ BC
∟A = ∟C ∟B = ∟D
О – точка пересечения диагоналей. АО = ОС ВО = ОD AC ┴ BD
∟A+∟B+∟C+ ∟D = (4 - 2) 1800 = 3600 ∟A+∟B = 1800 ∟B+∟C = 1800 ∟C+ ∟D = 1800 ∟A+∟D = 1800 ∟A+∟C = 1800 ∟B+∟D = 1800
a – сторона Трапеция. Трапеция – четырёхугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные — боковыми сторонами. 
АB ║ CD
∟A+∟B+∟C+ ∟D = (4 - 2) 1800 = 3600 ∟C+ ∟B = 1800 ∟A+∟D = 1800
2 а,b – стороны h - высота Равнобокая (равнобедренная) трапеция. Трапеция – четырёхугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной. Параллельные стороны трапеции называются основаниями, а непараллельные — боковыми сторонами. 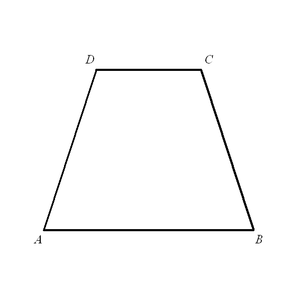
АB ║ CD
∟A =∟B ∟C =∟D.
AC = BD.
∟A+∟B+∟C+ ∟D = (4 - 2) 1800 = 3600 ∟C+ ∟B = 1800 ∟A+∟D = 1800
2 а,b – стороны h - высота Прямоугольная трапеция. Трапеция – четырёхугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные — боковыми сторонами. Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной. 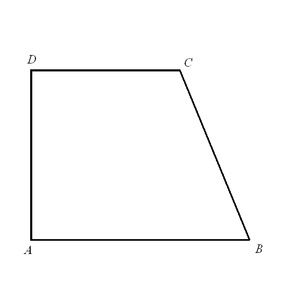
АB ║ CD AD ┴ AB AD ┴ DC
∟A =∟ D = 900
∟A+∟B+∟C+ ∟D = (4 - 2) 1800 = 3600 ∟C+ ∟B = 1800 ∟A+∟D = 1800
2 а,b – стороны h – высота, совпадает со стороной АD. |