Конспект урока алгебры в 8 классе по теме «Решение квадратных уравнений»
 Скачать 69.1 Kb. Скачать 69.1 Kb.
|
| Конспект урока алгебры в 8 классе по теме «Решение квадратных уравнений». Учебник: Алгебра. 8 класс под ред. А.Г. Мордковича. Тип урока: урок обобщающего повторения и систематизации знаний. Цели урока:
Оборудование: компьютер, проектор, презентация. Ход урока:
Тема нашего урока «Решение квадратных уравнений». Сегодня на уроке мы с вами повторим и закрепим знания и умения решения квадратных уравнений. Каждый из вас должен уметь правильно, быстро и рационально решать квадратные уравнения. Герберт Спенсер, английский философ, когда-то сказал: “Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы”. Проверим, кто из вас порадовал бы Герберта Спенсера.
Прежде, чем мы приступим к работе, повторим, что вы знаете по этой теме?
Историческая справка с презентацией, подготовленная учащимися (одним учащимся или группой учащихся). Представители различных цивилизаций: Древнего Египта, Древнего Вавилона, Древней Греции, Древней Индии, Древнего Китая, Средневекового Востока, Европы овладели приемами решения квадратных уравнений.
В алгебраическом трактате аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает шесть видов уравнений, выражая их следующим образом: квадраты равны корням, то есть ах2 = bх; квадраты равны числу, то есть ах2 = с; корни равны числу, то есть ах = с; квадраты и числа равны корням, то есть ах2 + с = bх; квадраты и корни равны числу, то есть ах2 + bх = с; корни и числа равны квадратам, то есть bх + с = ах2. Трактат Аль-Хорезми является первой дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения. Трактаты Аль-Хорезми были в числе первых сочинений по математике переведены в Европе с арабского на латынь. До XVI в. алгебру в Европе называли искусством алгебры и макабалы.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары: Обезьянок резвых стая Всласть поевши, развлекалась. Их в квадрате часть восьмая, Нна поляне забавлялась. А двенадцать по лианам... Стали прыгать, повисая... Сколько ж было обезьянок, Ты скажи мне, в этой стае? а) Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений. Решение задачи Бхаскары: (Решается учащимися в классе с помощью формул корней квадратного уравнения) Пусть было x обезьянок, тогда на поляне забавлялось – Составим уравнение: Х1=48; Х2=16 б) Затем учащимся предлагается решить самостоятельно еще одну задачу Бхаскары. Решают квадратное уравнение по теореме, обратной теореме Виета. Решение задачи Бхаскары: Сколько обезьян в стае, если квадрат пятой части, уменьшенной тремя, спрятался в пещере, и только одна осталась на виду, взобравшись на дерево? Решение: задача сводиться к решению квадратного уравнения  В заключении Бхаскара делает такое замечание: «Так как Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х2 + bх = с, при всевозможных комбинациях знаков коэффициентов b и с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
В школьном курсе математики подробно изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения, способ выделения квадрата двучлена, способ использования теоремы, обратной теореме Виета, графический способ. Имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Свойства коэффициентов квадратных уравнений: 1). Если а + в +с = 0 , то х1 = 1; х2 = с/а 2). Если а + с = в , то х1 = -1; х2 = - с/а Решите уравнения, используя эти свойства:
Ответы: 1вариант 1)1; 3/14. 2) -1;40. 3) -1;183/100. 2вариант 1)1:5/13. 2) 1; -24. 3) 1 -197/100.
Урок подходит к концу. Сегодня мы повторили все необходимые математические понятия, формулы и способы решения квадратных уравнений. Итогом нашего урока будет небольшая самостоятельная работа.
Тетради с решением учащиеся сдают на проверку.
Решить старинную задачу: На вопрос о возрасте одна дама ответила , что ее возраст таков, если его возвести в квадрат или умножить на 53 и из результата вычесть 696 , то получится одно и то же число. Список литературы:
|


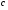 уравнение
уравнение  не имеет корней.
не имеет корней. 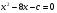 имеет два корня. Приведите пример.
имеет два корня. Приведите пример.