|
Конспект урока алгебры в 8 классе Автор: учитель математики Сахарова Н. К. 2012 Характеристики урока (занятие)
МБОУ «Средняя общеобразовательная школа № 5»
г. Вязники
«Решение задач с помощью рациональных уравнений»
конспект урока алгебры в 8 классе
Автор: учитель математики
Сахарова Н.К.
2012
Характеристики урока (занятие)
Уровень образования: основное общее образование
Целевая аудитория: учащиеся
Класс: 8 класс
Предмет: алгебра
Цель: создание условий для передачи опыта по применению деятельностного метода обучения на уроках математики при решении задач с помощью рациональных уравнений.
Задачи:
1. показать способы применения деятельностного метода обучения; 2.отследить эффективность открытого урока через рефлексию участников.
Используемое оборудование: проектор, компьютер, учебник «Алгебра» 8 класс «Просвещение» авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, под редакцией С.А.Теляковского.
Урок открытия нового знания. 8 класс, алгебра.
Тема: Решение задач с помощью рациональных уравнений.
Цели урока:
Обучающая:
закрепление понятия дробного рационального уравнения;
составление математической модели задачи, перевод условия задачи с обычного языка на математический;
умение проверять соответствие найденного решения условию задачи;
проверка уровня усвоения темы путем проведения проверочной работы.
Развивающая:
развитие умения правильно оперировать полученными знаниями, логически мыслить;
развитие интеллектуальных умений;
развитие умения принимать решения.
Воспитательная:
воспитание познавательного интереса к предмету;
воспитание самостоятельности при решении учебных задач;
воспитание воли и упорства для достижения конечных результатов.
Задачи: 1) актуализировать знание решения дробных рациональных уравнений, умение решать задачи при помощи рациональных уравнений; добиться усвоения алгоритма решения задач;
2) УУД: - Познавательные: овладение основами логического и алгоритмического мышления;
Регулятивные: развитие умения читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;
Коммуникативные: строить высказывания, аргументировано доказывать свою точку зрения;
Личностные: развитие навыков сотрудничества со сверстниками,
3) - воспитывать чувство товарищества.
Оборудование: презентация, конспект урока, компьютер, проектор.
Ход урока:
|
комментарии
|
1. Организационный момент.
Здравствуйте, ребята. Ещё начиная с начальной школы вы учились решать задачи. Для этого с каждым годом вы обучались всё новым и новым методам и способам решения. Сегодня мы познакомимся с задачами, решение которых сводится к дробным рациональным уравнениям.
Мотивация (самоопределение) к учебной деятельности.
- Работать сегодня мы будем в парах и индивидуально. Вспомните правила работы в парах. (Прислушиваться к мнению соседа, работать дружно, помогать друг другу)
В конце урока каждый из вас оценит свою работу и работу партнёра.
|
На данном этапе урока происходит вовлечение учащихся в деятельность на личностно-значимом уровне. Формируются личностные УУД.
Перейдём к следующему этапу урока.
|
Актуализация знаний.
Фронтальный опрос, устная работа с классом.
Ответьте, пожалуйста, на следующие вопросы:
-Какие уравнения называются дробными рациональными?
-Расскажите алгоритм решения дробных рациональных уравнений.
|
На этапе актуализации идёт повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося. Формируются регулятивные УУД.
|
3. Объяснение нового материала.
Прежде чем приступать к решению задачи необходимо несколько раз внимательно прочитать условие задачи, понять какую величину обозначить за неизвестную.
Рассмотрим пример.
Задача №618.
Из города в село, находящееся от него на расстоянии 120 км, выехали одновременно два автомобиля. Скорость одного была на 20 км/ч больше скорости другого, и поэтому он пришел к месту назначения на 1 ч раньше. Найдите скорость каждого автомобиля.
Решение. Составление математической модели:
Какой процесс описывается в задаче?
Какими величинами характеризуется этот процесс?
Как связаны между собой эти величины?
Сколько реальных процессов описывается в задаче?
Значение каких величин известны?
Значение каких величин сравниваются?
Значение каких величин требуется найти?
Обратить внимание учащихся, что любую из неизвестных величин можно обозначить за х?
х км/ч скорость первого автомобиля;
(х +20) км/ч – скорость второго автомобиля;
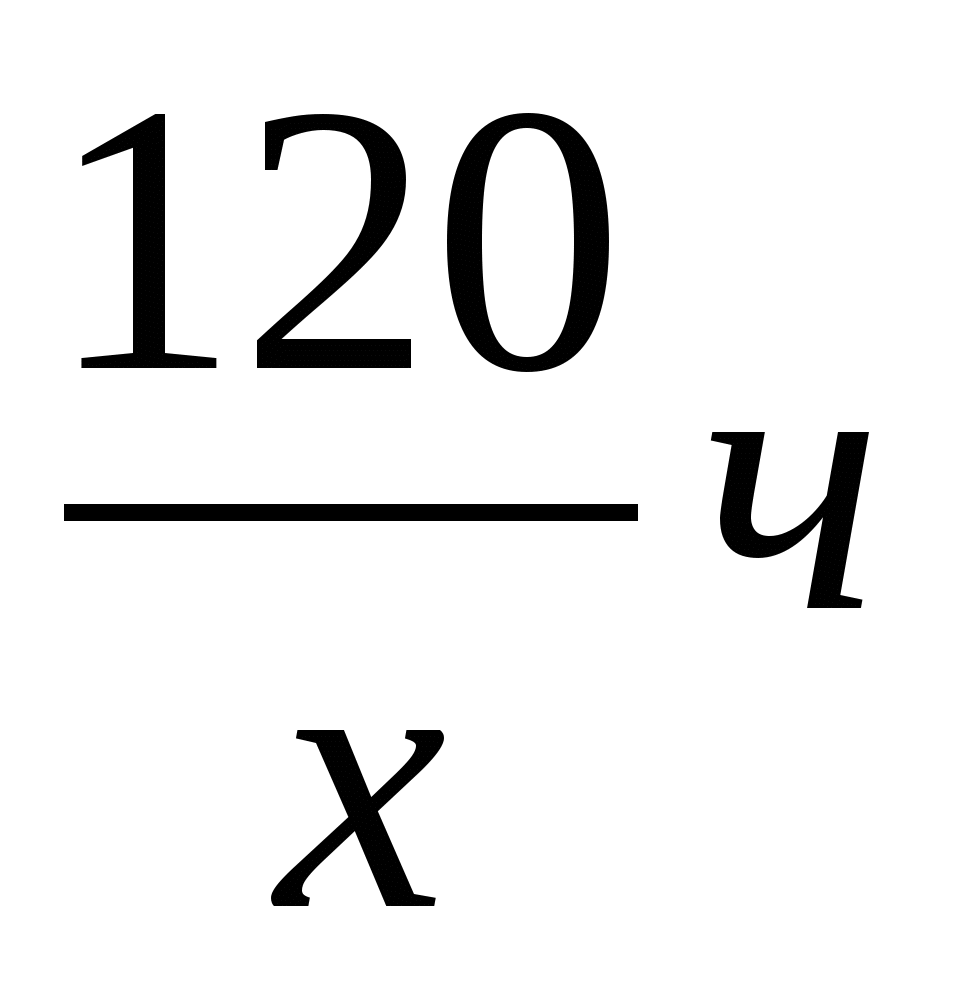 - время первого автомобиля; - время первого автомобиля;
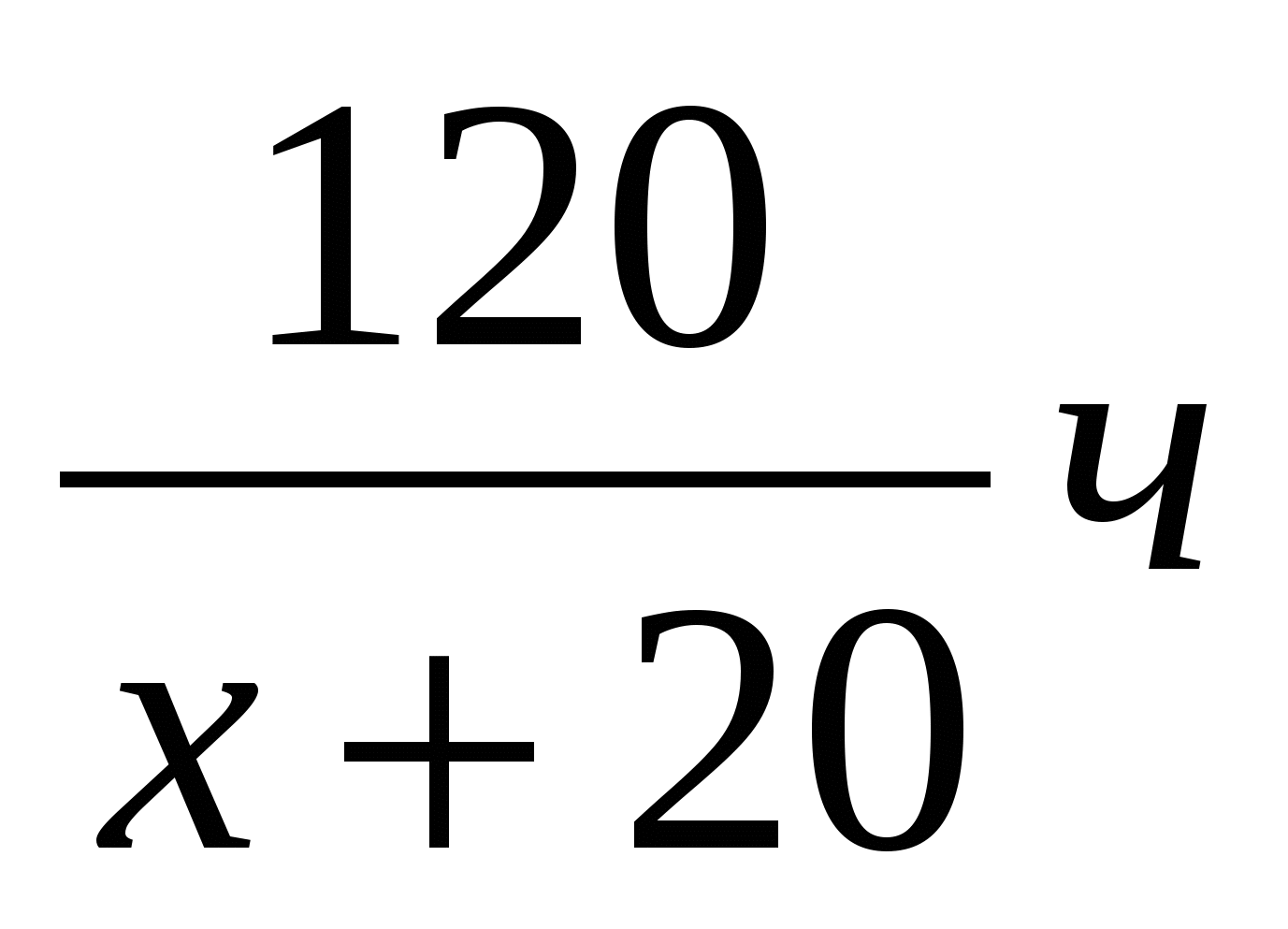 - время второго автомобиля. - время второго автомобиля.
Заполним таблицу:
|
V( км/ч)
|
t (ч)
|
S (км)
|
1 автомобиль
|
x
|
120/x
|
120
|
2 автомобиль
|
x+20
|
120/x+20
|
120
|
Согласно условию,
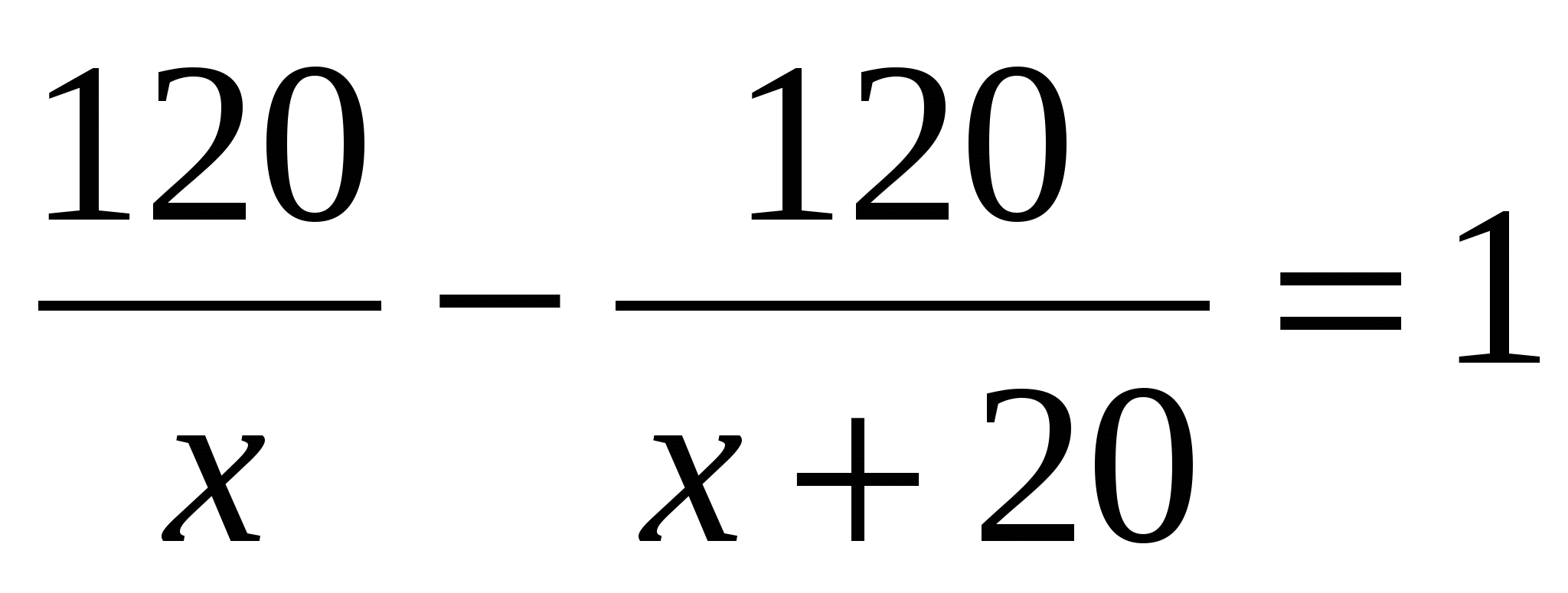 . .
Работа с составленной моделью.
Решив полученное уравнение, находим 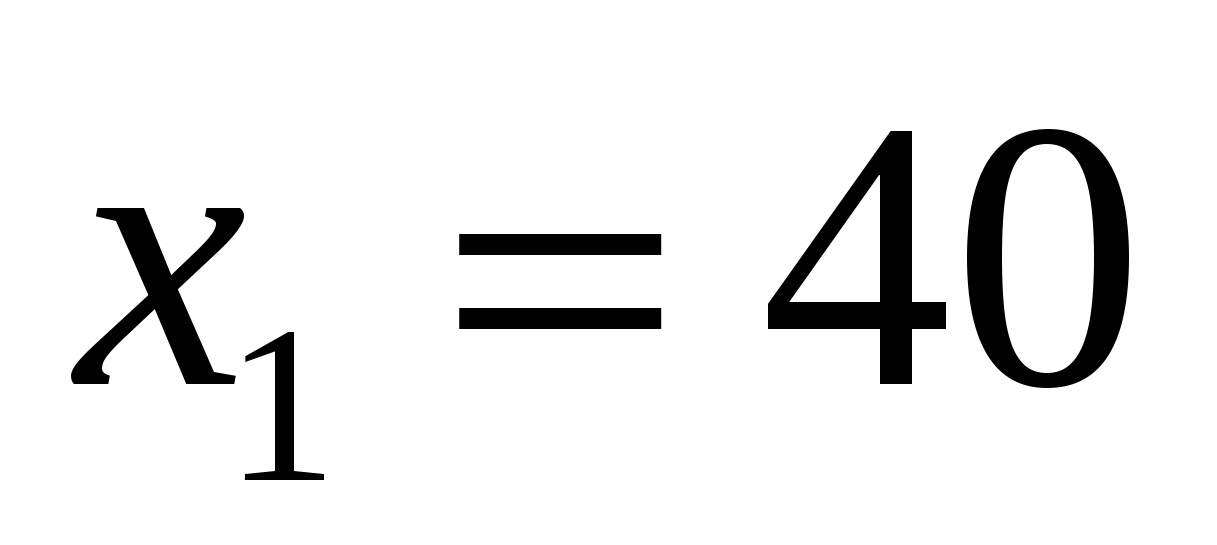 , , 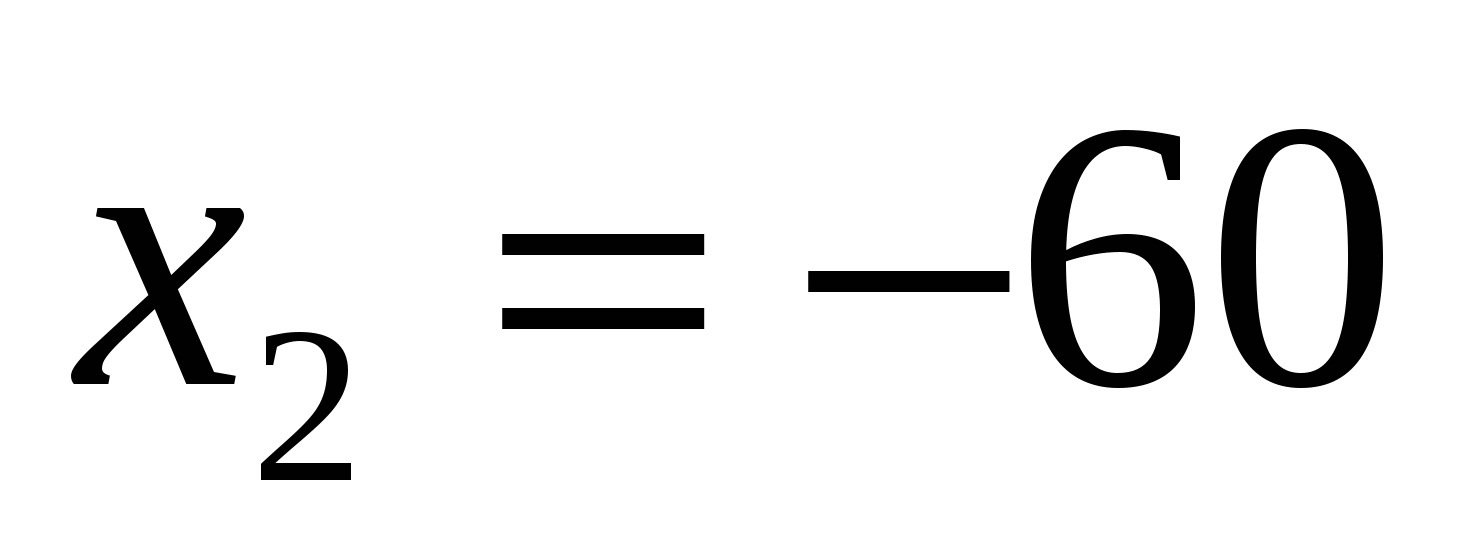 . -60 не удовлетворяет условию задачи. 40+20=60 км/ч . -60 не удовлетворяет условию задачи. 40+20=60 км/ч
Ответ на вопрос задачи.
После решения задачи необходимо ещё раз объяснить ход решения и поинтересоваться у учащихся, понятно ли им данное решение. Так же необходимо заметить, что в некоторых случаях целесообразно создавать геометрические модели для лучшего восприятия условия задачи. Чаще всего такие модели составляются к задачам на движение. ( Как пример разобрать задачу № 620)
|
На данном этапе дети учатся добывать информацию различными способами: наблюдение, чтение, слушание .Происходит открытие нового знания. Формируются познавательные УУД.
Учатся доносить свою позицию до других (строить высказывания, пользуясь математической терминологией), слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения, при необходимости отстаивать свою точку зрения, аргументировать её. Формируются коммуникативные УУД,
Учитель проверяет решение задачи, учащиеся комментируют, как решали задачу.
|
4.Первичное закрепление с проговариванием во внешней речи
Работа в тетрадях. Задания из учебника «Алгебра 8», Ю.Н. Макарычев,2010:
№620 . Учитель контролирует выполнение задания, отвечает на возникшие вопросы, оказывает помощь слабоуспевающим ученикам. Учащиеся работают парами вместе обсуждают решение задачи.
(Дети читают текст задачи, делают выводы)
|
На данном этапе формируются познавательные УУД: использовать полученную информацию в деятельности, развитие мыслительных операций, решать задания по аналогии, используя алгоритм действий, дети учатся самостоятельно применять знания в новой ситуации. Формируются регулятивные УУД. Каждый делает для себя вывод, что он уже умеет. Формируются личностные УУД (самоконтроль, самооценка, саморефлексия, способность к саморазвитию)
|
5. Выполнение контролирующего задания по изученной теме и включение в систему знаний повторение.
Индивидуальная работа выполняется на листочках.
Вариант 1.
Выполните тест, выбрав в заданиях 1-3 ответы под цифрами 1,2,3 или 4 ( ответы указаны в рамке),а в заданиях 4-5 запишите получившийся у вас результат в виде целого числа или десятичной дроби. Желаем удачи.
Среди данных уравнений выберите те, которые являются дробными рациональными :
А)  ; Б) ; Б) 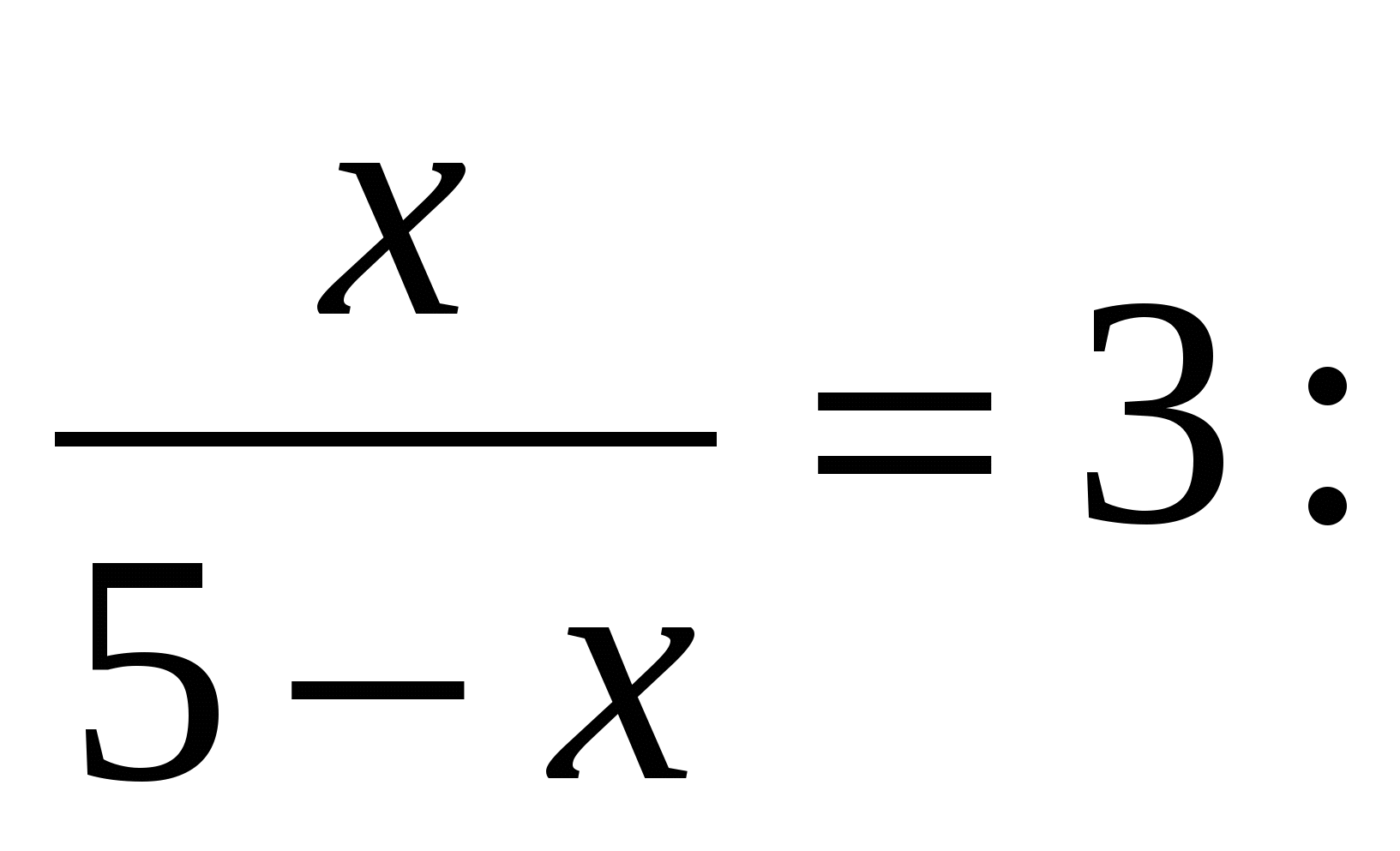 В) В) 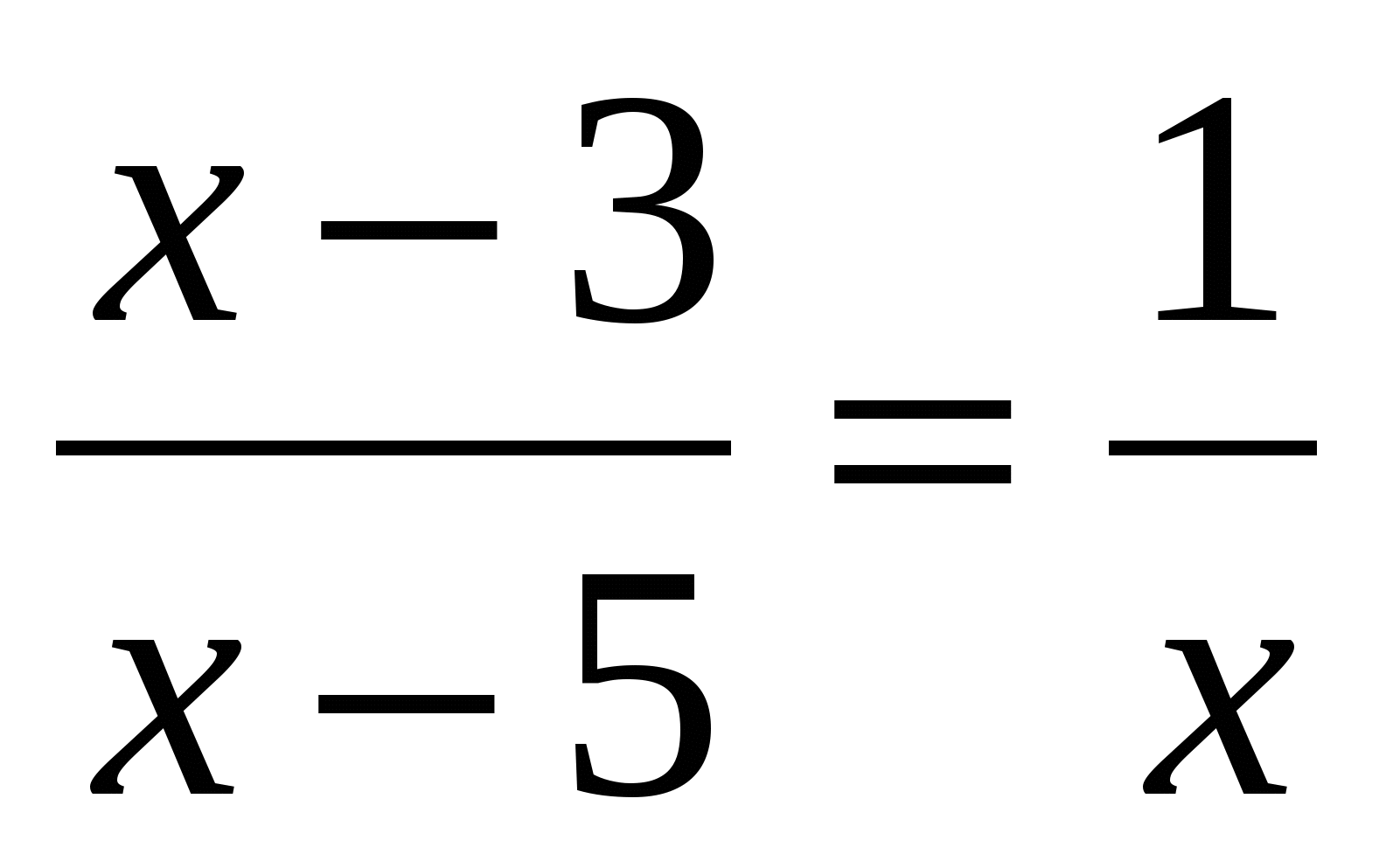 ; Г) ; Г) 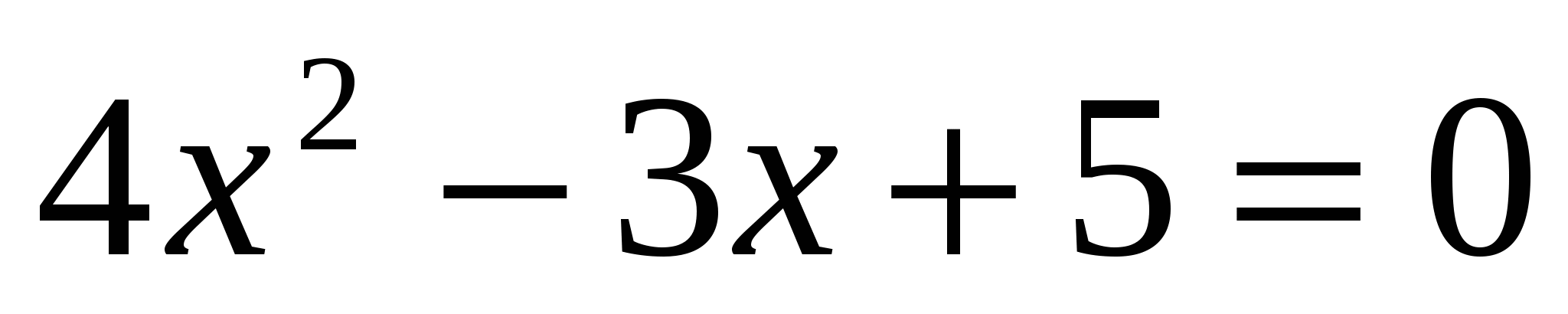
-
1) А ; 2) Б и В ; 3) Г ; 4) А,Б и В
|
Решите уравнение: 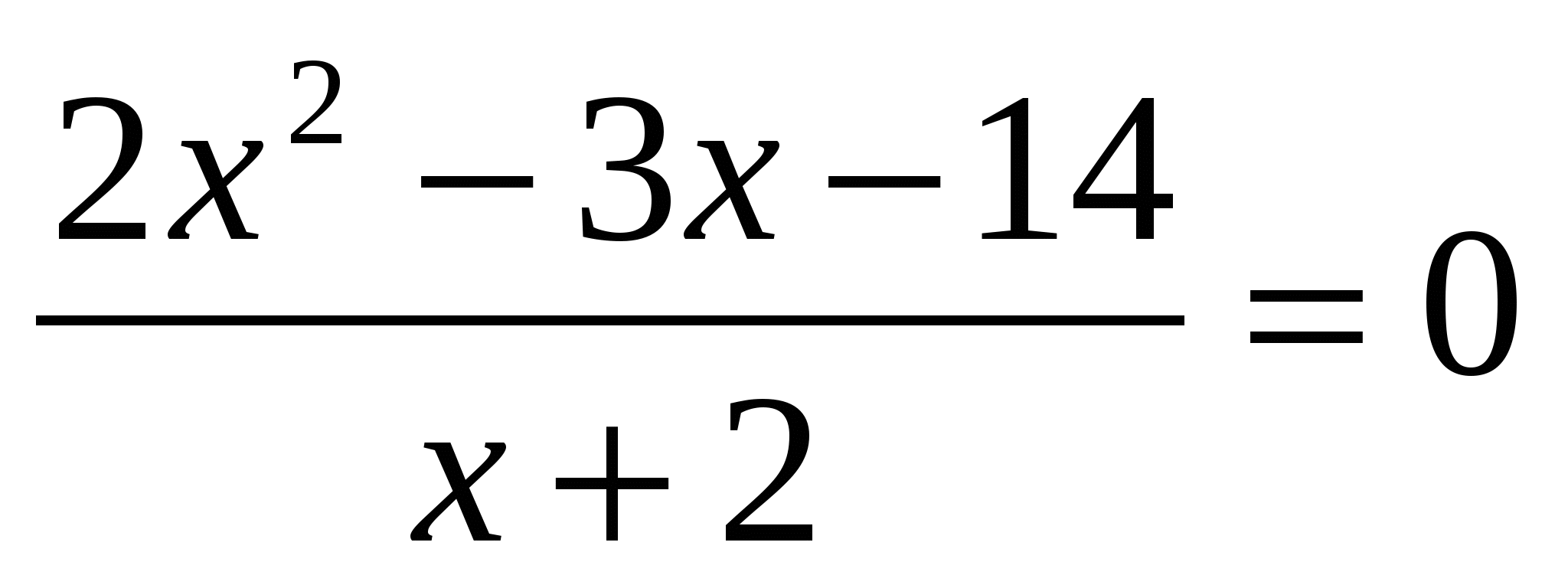
-
1) 7 ; -2 ; 2) 7 ; 3) 3,5 ; 4) 3,5 ; -2
|
Прочитав условие задачи, составьте уравнение, которое ему соответствует:
Теплоход прошёл 108 км по течению реки и 84 км против течения, затратив на весь путь 8ч. Найдите собственную скорость теплохода, обозначив её х км/, если скорость течения реки 3 км/ч
-
Решите уравнение и в ответ укажите его наименьший корень
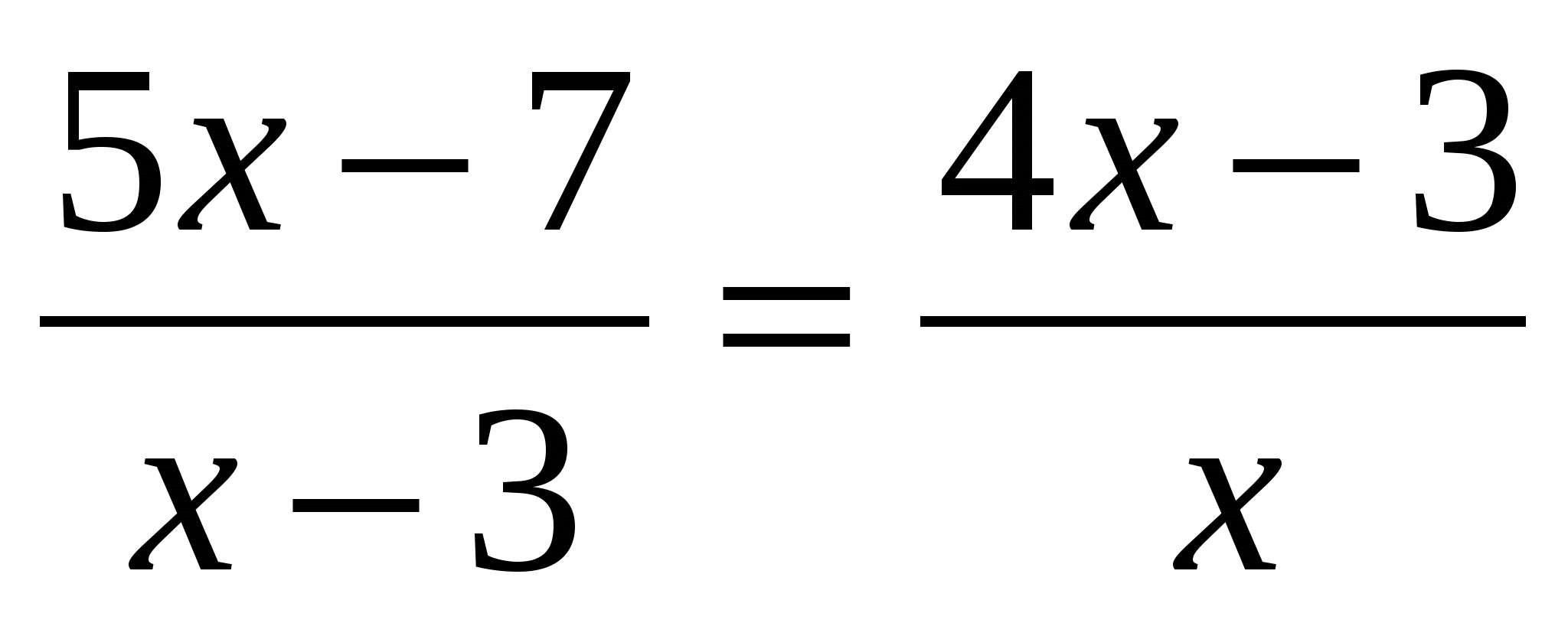
Ответ:__________
Найдите корень уравнения
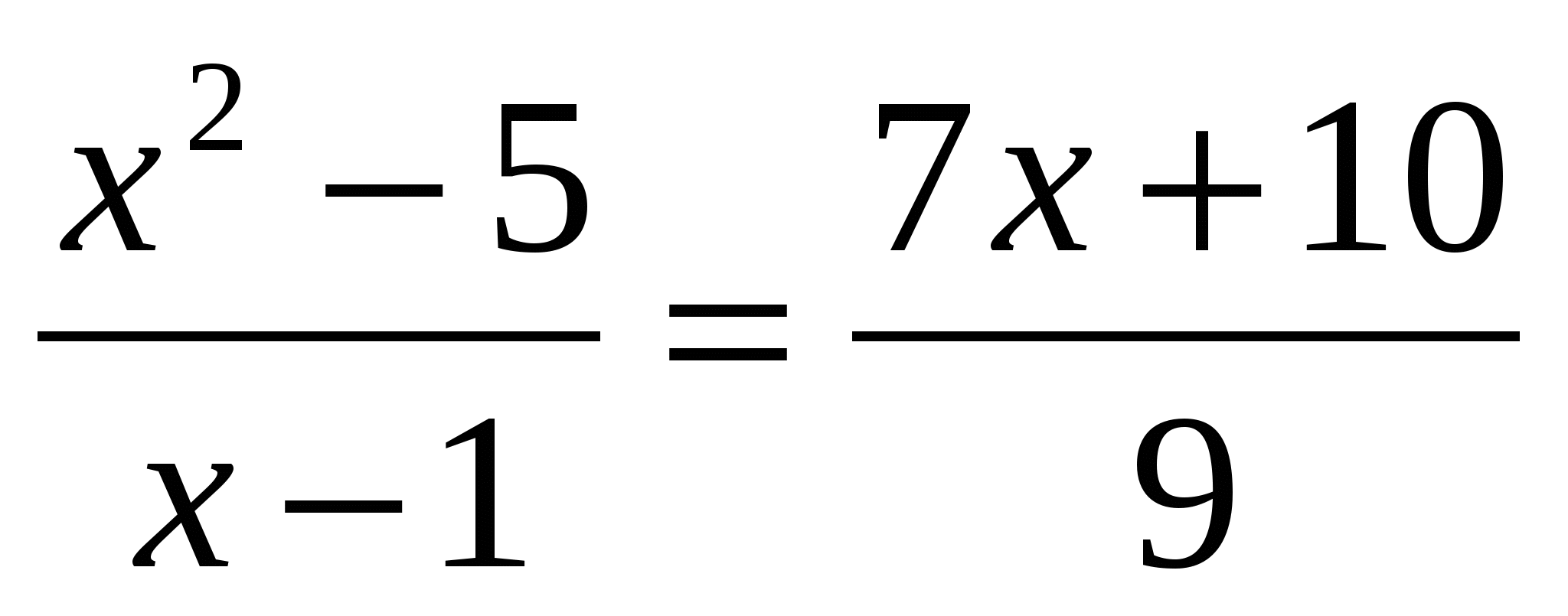
Ответ: ___________
Вариант 2.
Выполните тест, выбрав в заданиях 1-3 ответы под цифрами 1,2,3 или 4 ( ответы указаны в рамке),а в заданиях 4-5 запишите получившийся у вас результат в виде целого числа или десятичной дроби. Желаем удачи.
Среди данных уравнений выберите те, которые являются дробными рациональными :
А) 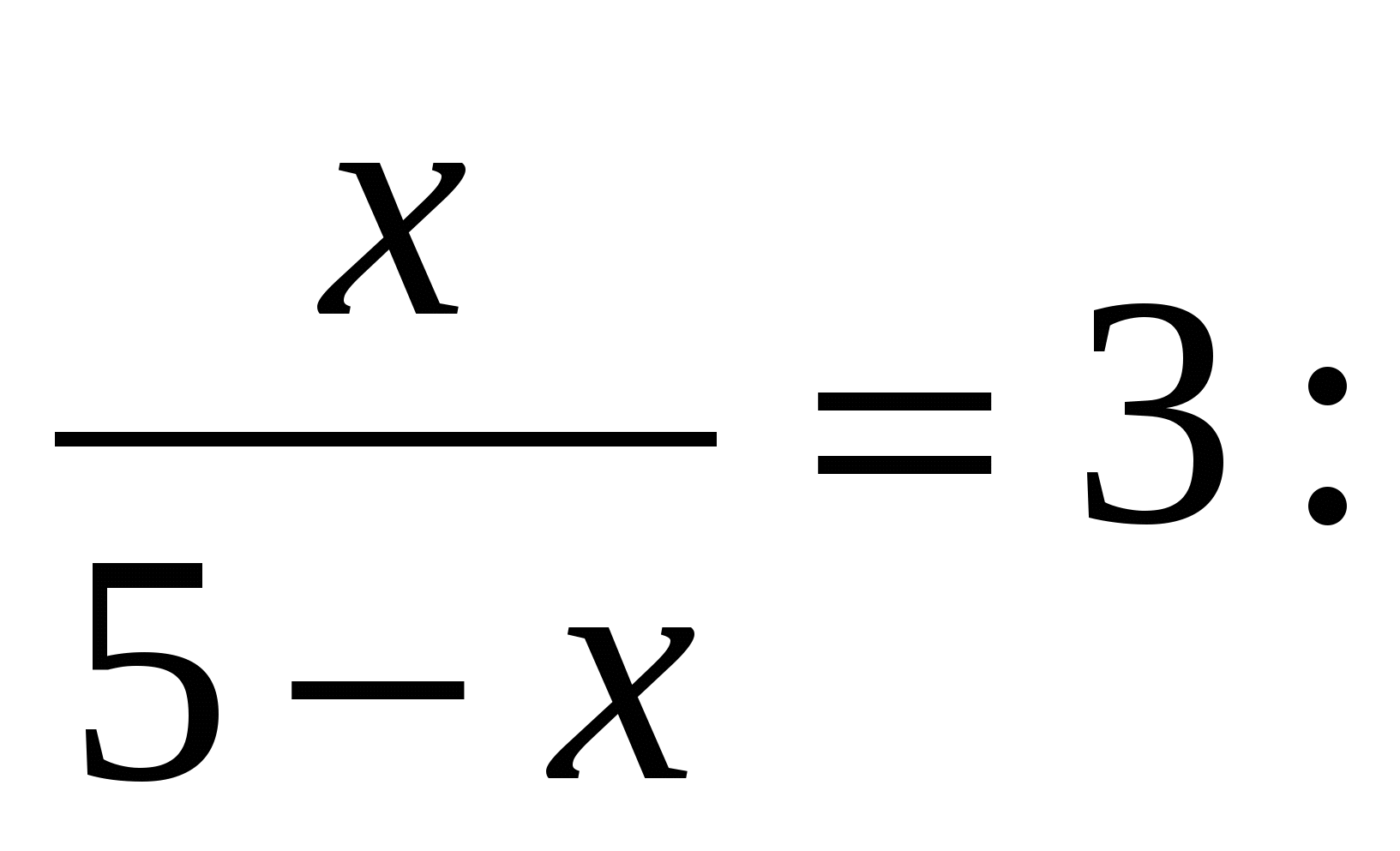 ; Б) ; Б)  В) В) 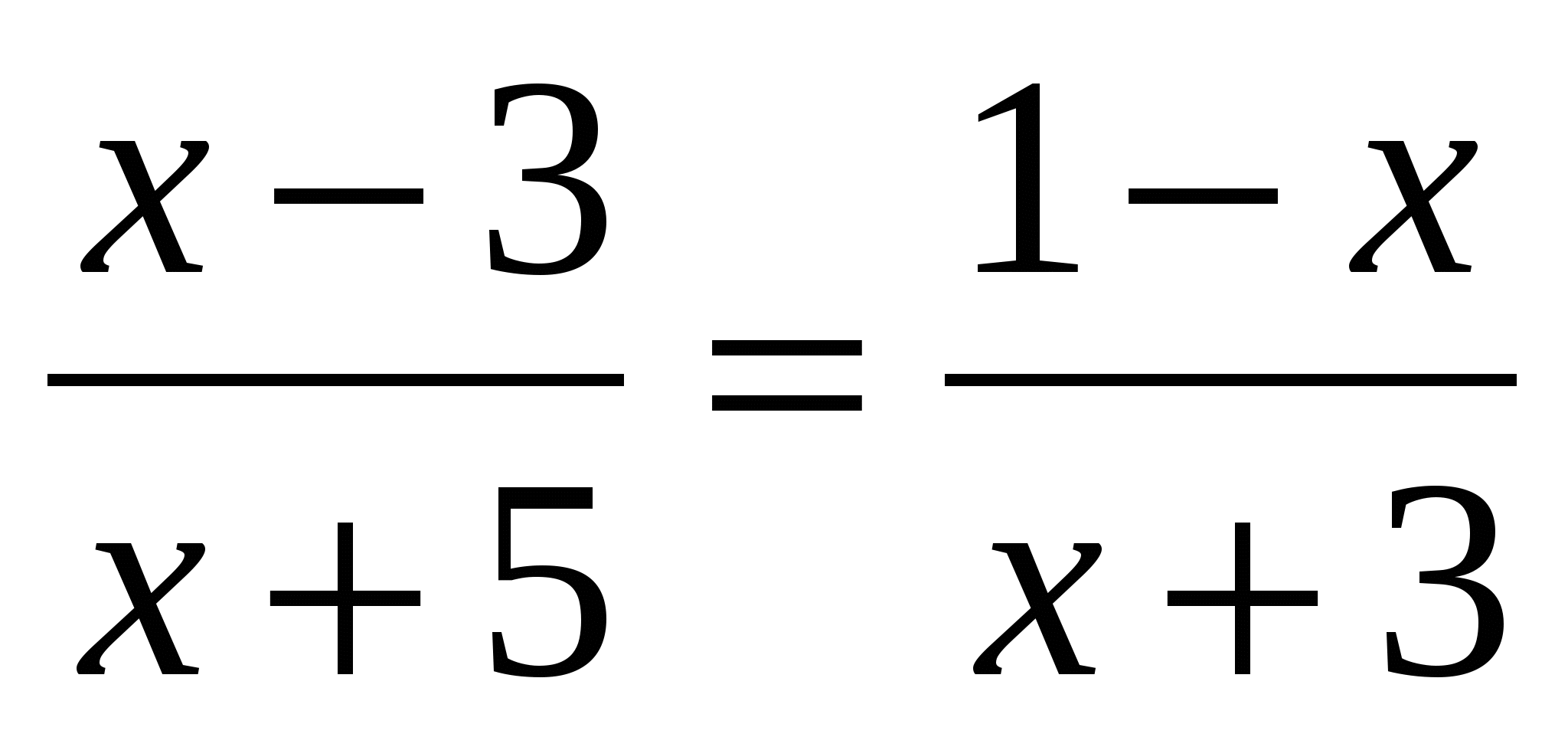 ; Г) ; Г) 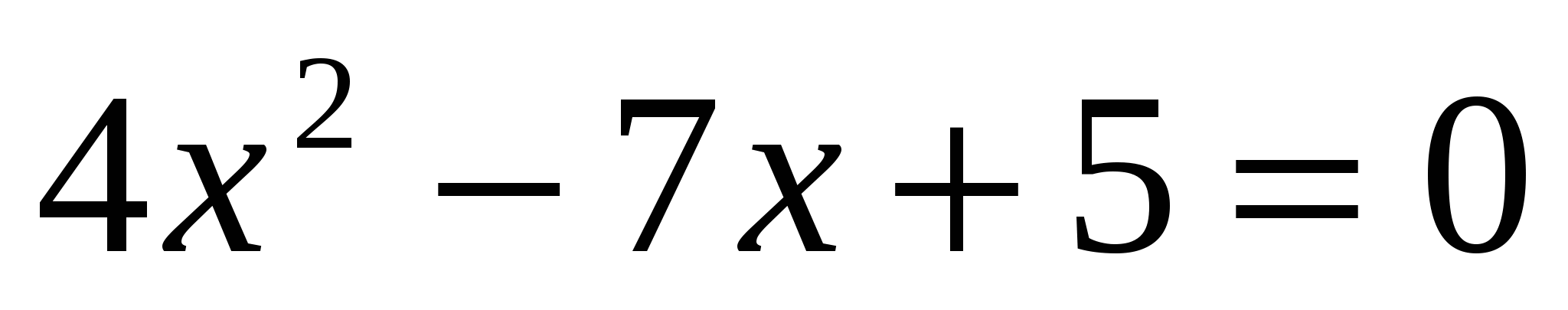
-
1) А и В ; 2) Б ; 3) В и Г ; 4) Б и Г
|
Решите уравнение: 
-
Прочитав условие задачи, составьте уравнение, которое ему соответствует:
Моторная лодка прошла 56 км против течения реки и 32 км по течению, затратив на весь путь 3ч. Найдите собственную скорость лодки, обозначив её через х км/ч, при условии, что скорость течения реки равна 1км/ч.
-
Решите уравнение и в ответ укажите его наибольший корень
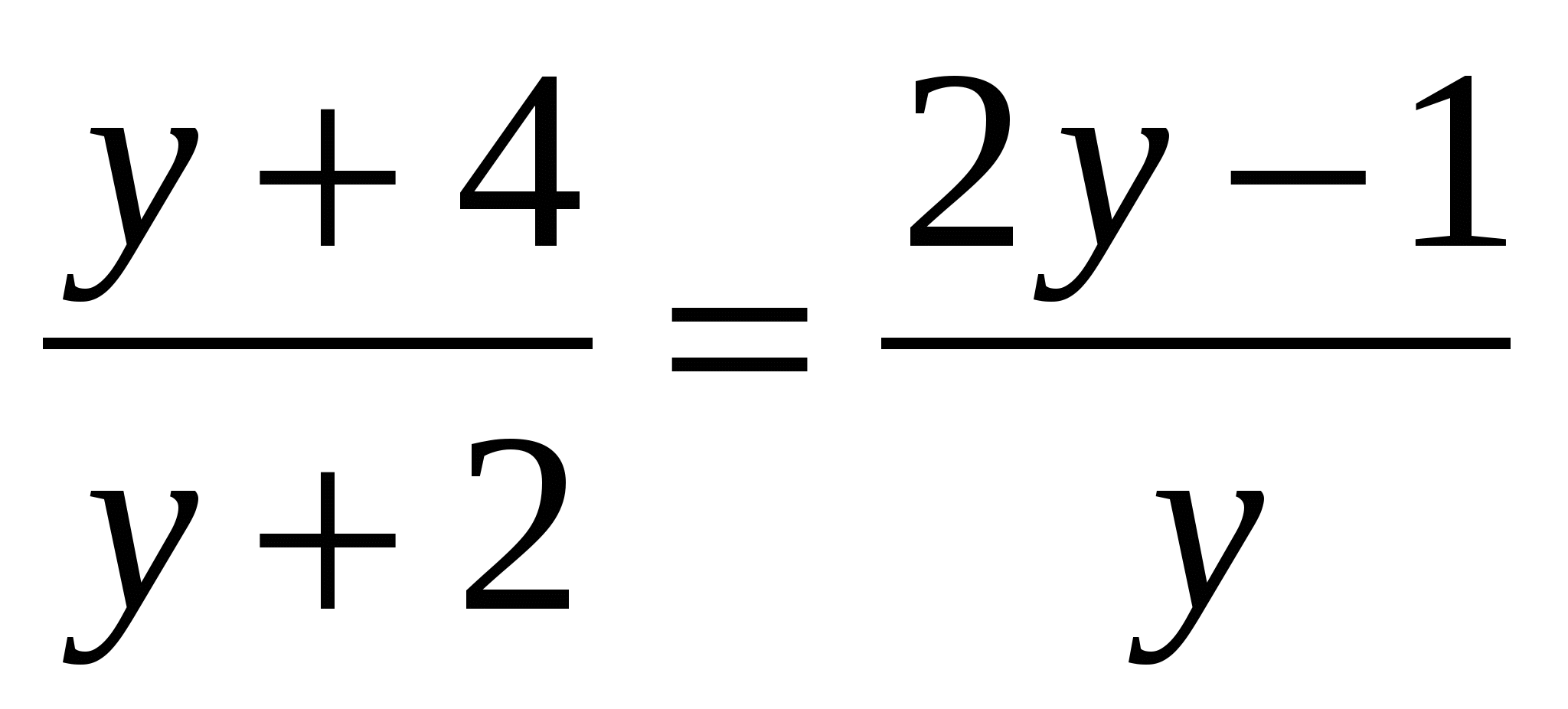
Ответ:__________
Найдите корень уравнения
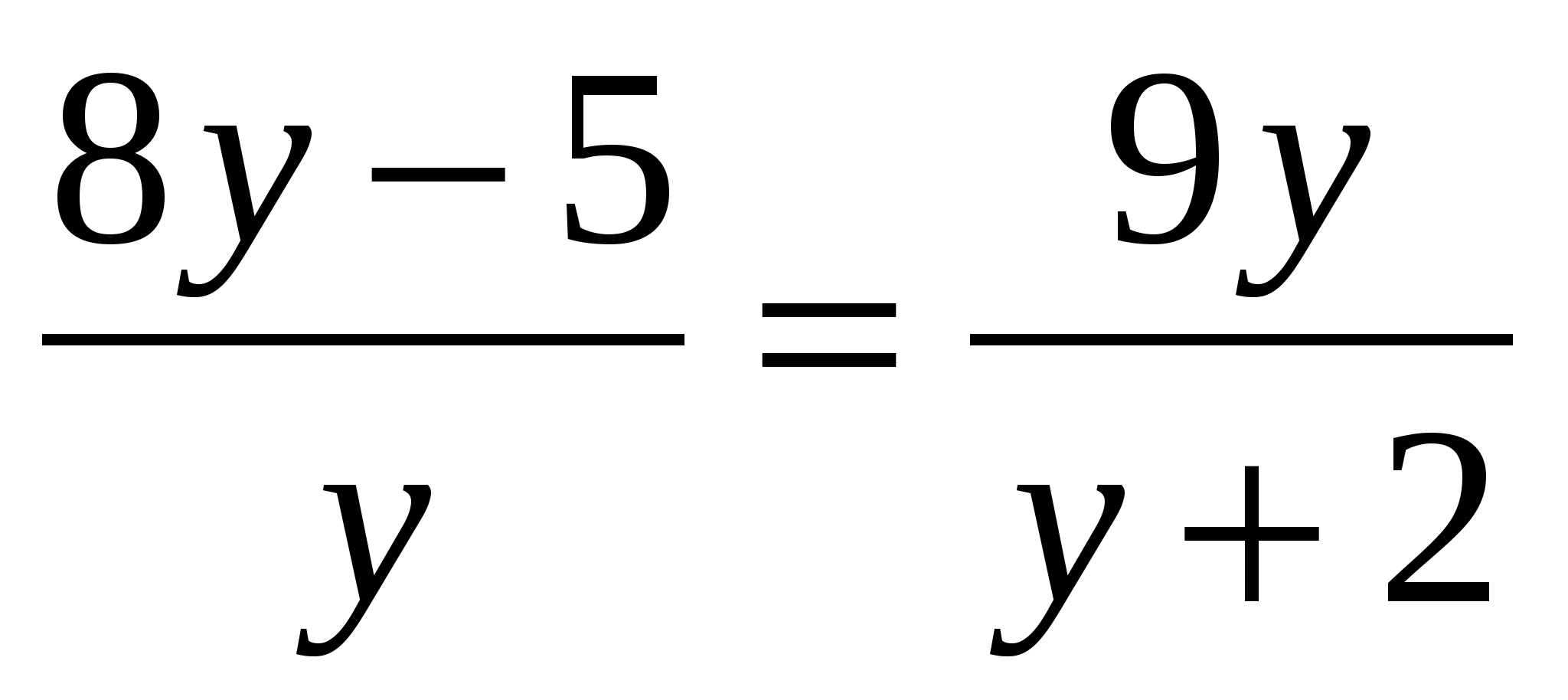
Ответ: ___________
|
На данном этапе предлагаются не только задания, при решении которых используется новый алгоритм, но и выполняются задания, в которых новое знание используется вместе с ранее изученным. Выполняются универсальные логические действия: анализ, синтез.
Дети учатся находить информацию в тексте задачи, выделять главное, применять новые знания в другой ситуации. Формируются познавательные УУД.
|
Домашнее задание .
Прочитать п.26 из учебника, разобрать примеры.
№ 619; №625.
|
Д/з включает в себя как репродуктивное задание, так и творческое, что позволяет вызвать у детей познавательный интерес. Формируются познавательные УУД,
|
Рефлексия УД на уроке.
- Итак, над какой темой мы работали? Удалось ли решить поставленную задачу? Каким способом? Какие получили результаты? Что нужно сделать ещё?
- В чём испытывали трудности?
- Где можем применить новые знания? (При решении задач)
- Оцените работу вашего партнёра и себя .
Молодцы. Спасибо за урок.
|
В диалоге с учителем дети учатся определять степень успешности выполнения своей работы и работы партнеров, осознание своей УД. Понимать причины своего неуспеха и находить способы выхода из этой ситуации. Регулятивные УУД.
|
|
|
|
 Скачать 91.22 Kb.
Скачать 91.22 Kb.