Ключи Пятый класс
 Скачать 44.32 Kb. Скачать 44.32 Kb.
|
| Ключи Пятый класс 5.1. Ответ. 13. Решение. Уберем самого правого мальчика. Тогда мальчиков и девочек будет поровну, то есть по 12. Значит, в шеренге стояло 12 + 1 = 13 мальчиков. 5.2. Ответ. 1111 + 888 + 11 + 4 = 2014. 5.3. Решение. Из прямоугольника 6x1 и квадрат 1x1 сложим прямоугольник 7x1. Аналогично сложим прямоугольники 7x1 из пар прямоугольников 5x1, 2x1 и 4x1, 3x1. Из четырех полученных прямоугольников 7x1 складывается прямоугольник 7x4. 5.4. Ответ. На расстоянии 10 км. Решение. За 3 часа, с 9.00 до 12.00, Юра прошёл 18 км. Если он пройдет еще два километра, то он попадет домой. То есть 18 + 2 = 20 км. – это путь до места разворота и обратно. Значит, он развернулся на расстоянии 20:2 = 10 км от дома. 5.5. Ответ. 484. Решение. На каёмке, не считая угловых, лежит 84 – 4 = 80 плиток. Значит, на каждой стороне лежит 20 плиток, не считая угловых, а вместе с угловыми – 22 плитки. Поэтому общее число плиток равно 484. Шестой класс 6.1. Ответ. Например: 9 + 6; 8 + 5 + 2; 7 + 4 + 3 + 1. Решение. Суммарный вес гирек равен 45, поэтому в каждой коробочке суммарный вес гирек равняется 15 г. 6.2. Ответ. Борис. Решение. Так как мальчик дал три разных ответа, он хотя бы два раза соврал. Поэтому два дня из трёх, когда мальчику задавали вопросы, пришлись на нечётные числа. Поскольку чётные и нечётные числа месяца чередуются, это должны были быть первый и третий дни. Стало быть, второй день пришёлся на чётное число. В этот день мальчик и назвал своё настоящее имя. 6.3. Ответ. Мышь – 140г, сыр – 10г, мышонок – 30г. Решение. Из условия следует, что удвоенный вес мыши равен 180 + 100 = 280г. Поэтому вес мыши равен 140г. Тогда мышонок и сыр вместе весят 180 – 140 = 40г. А вес сыра, согласно условию, равен четверти этого веса. 6.4. Решение. Два способа сделать это показаны на рис. 1. Есть и другие способы. 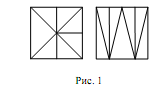 6.5. Решение. Разобьем палочки на три группы: от 1 до 8, от 9 до 16, от 17 до 24. В каждой группе первую палочку соединим с последней, вторую – с предпоследней, третью – с третьей с конца, оставшиеся две палочки тоже соединим. Получим в каждой группе по четыре одинаковых палки, из которых сложим квадрат. Стороны полученных квадратов: 9, 25, 41. Замечание. Есть и другие способы сложить три квадрата. Седьмой класс 7.1. Ответ. 6. Решение. Допустим, что гостей действительно больше шести. Тогда правы и Вася, и его сестра, а это противоречит условию задачи. Значит, гостей не больше шести и Вася неправ. Но тогда должна быть права сестра, иначе снова нарушится условие задачи. Значит, гостей больше пяти. Но если их больше пяти и не больше шести, то их ровно шесть. 7.2. Решение. При первом взвешивании на одну из чашек весов кладем гирю и все гвозди раскладываем по чашкам так, чтобы установилось равновесие. Получим 13 и 12 кг гвоздей. Первую кучку откладываем, а остальные гвозди делим пополам, взвешивая без гири: 12 = 6 + 6. Получили искомое количество гвоздей: 19 = 13 + 6. 7.3. Ответ. 1, 3, 5, 10. Решение. В сумме 9 + 14 + 16 + 18 = 57 вес каждого орешка сосчитан трижды, значит, суммарный вес всех орешков равен 19 г. Разность 19 – 9 = 10 – это вес одного из орешков. Аналогично находим веса остальных орешков. 7.4. Ответ. 400. Решение. Сумма длин короткой и длинной сторон прямоугольника равна 20. Но эта сумма равна стороне исходного квадрата. 7.5. Ответ. Нельзя. Первое решение. Допустим, можно. Возьмём красный шарик, не лежащий с краю (такой найдётся хотя бы в пятёрке шариков со 2-го по 6-ой). Соседние с ним шарики должны быть белыми, иначе найдутся два соседних шарика, среди которых нет белых. Но это значит, что мы нашли три подряд идущих шарика, среди которых нет синего. Второе решение. Разбив 30 шариков на 15 пар соседних шариков, убеждаемся, что среди выложенных шариков не меньше 15 белых. Разбив их на 10 троек подряд идущих шариков, убеждаемся, что среди выложенных шариков не меньше 10 синих. Наконец, разбив их же на 6 пятёрок подряд идущих шариков, видим, что среди выложенных шариков не меньше 6 красных. Получается, что шариков должно быть не меньше, чем 15 + 10 + 6 = 31, а их только 30. Восьмой класс 8.1. Ответ. 49 рублей 50 копеек. Решение. Пусть вначале у Васи было x рублей. Из условия задачи получаем, что x + 49 = 99x. Решая это уравнение, получаем x = 0,5 рубля = 50 копеек. 8.2. Ответ. 70. Первое решение. Склеим все бревна в одно 100-метровое бревно. Чтобы его разделить на 100 частей, нужно сделать 99 распилов, из которых 29 уже было сделано. Второе решение. Если было m трехметровых и n четырехметровых бревен, то m + n = 30, 3m + 4n = 100, откуда m = 20, n = 10. Поэтому нужно сделать 202 + 103 = 70 распилов. 8.3. Ответ. a = 2. Первое решение. Заметим, что при x = 1 выполняется ax + 1 = x + a = a + 1, так что точка M (1; a + 1) является общей для прямых y = ax + 1 и y = x + a. Так как прямые различны, M – их единственная общая точка. Поэтому прямая y = 3 тоже должна проходить через неё, откуда a + 1 = 3 и a = 2. Легко видеть, что при a = 2 все три прямые действительно различны. Второе решение. По условию в точке пересечения a x + 1 = x + a ↔ (a – 1)( x – 1) = 0, откуда a = 1 или x = 1. Но случай a = 1 невозможен, потому что тогда первые две прямые совпадали бы. Дальше рассуждаем как в первом решении. 8.4. Ответ. 90°, 60°, 30°. Решение. ∟ADB = 180° – ∟ADC = 60°. Тогда ∟ABD = 60°. Значит, треугольник ABD – равносторонний. Откуда AD = BD = DC. То есть треугольник ADC – равнобедренный. Значит, ∟DAC = ∟DCA = 30°. Следовательно, ∟BAC = 90°. 8.5. Ответ. 1003. Решение. Заметим, что два воина, стоящие рядом, не могли оказаться рыцарями. Действительно, если бы они оба были рыцарями, то они оба сказали бы неправду. Выберем воина, стоящего слева, и разобьем ряд из оставшихся 2004 воинов на 1002 группы по два рядом стоящих воина. В каждой такой группе не более одного рыцаря, т. е. среди рассматриваемых 2004 воинов не более 1002 рыцарей, т. е. всего в шеренге не более 1002 + 1 = 1003 рыцарей. Рассмотрим шеренгу РЛРЛР...РЛРЛР. В такой шеренге стоит ровно 1003 рыцаря. Девятый класс 9.2 9.1  9.3  9.4   9.5 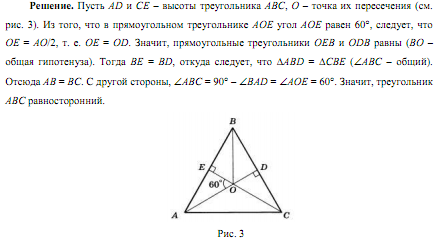 10.1 Десятый класс 10.2  10.3  10.4  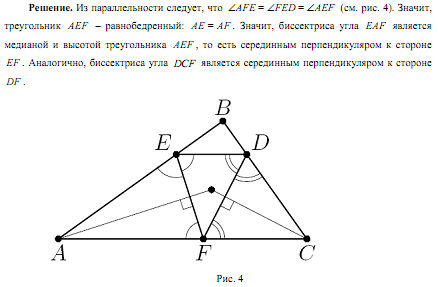  10.5  11.1 Одиннадцатый класс 11.2  11.3  11.5 11.4   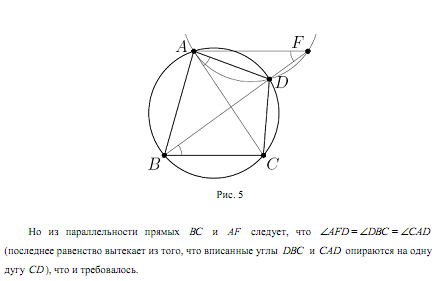 |