Исследовательская работа Признаки равенства треугольников Секция: математика
 Скачать 123.49 Kb.
|
| VI городская научно-исследовательская конференция учащихся и студентов «Шаг в будущее» Научно – исследовательская работа Признаки равенства треугольников Секция: математика Выполнил: Копьёв Никита Олегович город Новый Уренгой Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 11» 8б класс Научный руководитель: Волкова Любовь Николаевна, Учитель алгебры и геометрии город Новый Уренгой Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 11» Новый Уренгой 2011год Содержание работы: Введение…………………………………………………………………………………………3 Описание методики исследования…………………………………………………………...5 Вывод и рекомендации.………………………………………………………………………10 Список литературы……………………………………………………………………………11
Треугольник – одна из основных фигур в планиметрии. При решении задач используют его самые разнообразные свойства. Свойства треугольника широко применяют на практике. Например, в архитектуре: при разработке чертежа здания, при планировке будущих квартир; в промышленности: при проектировании различны деталей, при изготовлении стройматериалов, при строительстве морских и авиа судов; в навигации: для проложения правильного и максимально точного маршрута; в астрологии и астрономии, одним словом просто необходимо знать треугольник и все его свойства. Одно из важнейших свойств для пары треугольников, устанавливать их равенство. Существует ряд задач на тему установления равенства двух треугольников. Для решения задач такого рода, необходимо знать признаки равенства треугольников. В школьном курсе изучается только 3 признака равенства треугольников.
Уточнение количества признаков равенства треугольников (анализ). Помимо трёх основных признаков равенства треугольников возможно указать немало других. Какие именно три соответствующих элемента нужно назвать для установления равенства треугольников?
Изучение признаков равенства треугольников.
Треугольник, как одна из основных фигур в планиметрии.
Расширить и углубить знания о конструкции (основе) создания признаков равенства треугольников.
Теоретический (изучение, анализ и синтез), системно-поисковый, практический (доказательство теорем).
Возможно ли сформулировать, кроме трёх известных, другие признаки равенства треугольников?
При изучении этого вопроса, нами было прочитано множество литературы. Во всех энциклопедиях в рамках изучения признаков равенства треугольников описывались лишь 3 признака равенства треугольников. В учебниках за седьмой класс так же предложены к изучению только 3 признака. И лишь в Справочнике по элементарной математике М.Я.Выгодского были предложены 4 признака.
Древнегреческий историк Геродот оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. По летописи Геродота, с этого началась геометрия – «землемерие». Такое название связанно с применением геометрии для измерений на плоскости. Древние землемеры выполняли различные геометрические построения, измеряли длинны и площади; астрологи рассчитывали расположение небесных светил, - всё это требовало весьма обширных познаний о свойствах плоских и пространственных фигур в первую очередь о треугольнике.
Треугольник – это одна из основных фигур в геометрии. Знакомый всем треугольник по праву считается простейшей из плоских фигур: любая плоская, т.е. простирающаяся в двух измерениях, фигура должна содержать хотя бы три точки, не лежащие на одной прямой. Если соединить эти точки попарно прямолинейными отрезками, то построенная фигура и будет называться треугольником. Так же называют и заключённую внутри образовавшегося контура часть плоскости. Признаки равенства треугольников. Начнём с определения. Треугольники ABC и A1B1C1 называются равными, если они имеют соответственно равные стороны и углы, т.е. сторона АВ равна стороне А1В1, угол при вершине А первого треугольника равен углу при вершине А1 второго треугольника , угол при вершине В равен углу при вершине В1 второго треугольника, угол при вершине С равен углу при вершине С1 второго треугольника, сторона ВС равна стороне В1С1, сторона АС равна стороне А1С1. Можно назвать и иное определение, применяемое к любым фигурам: треугольники равны, если присутствует движение, приводящее один из них в другой.  В В1А С А1 С1 Треугольник состоит из шести элементов. Из трёх углов и трёх сторон. При этом возникает вопрос: «Какого наименьшее количество элементов треугольника нужно взять для установления равенства двух треугольников?» Мы не сможем установить равенство двух треугольников по одному элементу, потому что неизвестно: «Будут ли равны остальные элементы?» В В1      А С А1 С1АС = А1С1 Так же невозможно установить равенство двух треугольников, используя два элемента по причине нехватки информации для установления равенства. В      В1А С А1 С1АВ = А1В1, АС = А1С1. Однако, при этом возможно установление равенства двух треугольников используя три элемента. Но при этом возникает вопрос: «Какие именно три элемента нужно назвать, для установления равенства двух треугольников?» Возможны следующие тройки элементов:
Первым трём соответствуют признаки равенства треугольников, которые учащиеся традиционно изучают в седьмом классе, а вот остальные следует проверить. Итак, мы попытались найти ответ методом подбора. С этой целью мы оставили теоремы и попытались доказать их. Первая теорема. Формулировка: если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники равны.   В Дано: АВС, А1В1С1,   В1 В = В1, А = А1, С = С1. Доказать: АВС = А1В1С1.А С А1 С1 Доказательство:  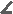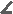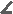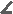Пусть у треугольников АВС и А1В1С1, А = А¹, В = В¹, С = С¹; попробую доказать, что треугольники равны. Так как А = А1, то вершина А совпадёт с вершиной А1, при этом совместятся лучи АС с А1С1 и АВ с А1В1(рис.1). Но так как мы не знаем = А1В1, или нет, нельзя утверждать, что вершина В совпадёт с вершиной В1, следовательно в данном случае невозможно утверждать, что треугольники равны. Значит теорема не верна.В  В1 А(А1) С 1 С Рисунок № 1 Вторая теорема. Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны. Но в этой теореме есть один нюанс: угол может лежать против большей из представленных сторон, а может лежать против меньшей из представленных сторон. Мы рассмотрим оба случая. Первый случай. Формулировка: если две стороны и угол, лежащий против меньшей стороны, одного треугольника соответственно равны двум сторонам и углу, лежащему против меньшей стороны, другого треугольника то такие треугольники равны. А     Дано: АВС , А¹В¹С¹,АВ = А¹В¹, ВС = В¹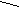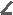С¹,    А1 С = С¹. Доказать: АВС = А1В1С1.В С В1 С1 Доказательство: 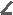 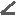Пусть у треугольников АВС и А1В1С1, АВ = А1В1, ВС = В1С1, С = С1, попробуем доказать, что треугольники равны.Так как С = С1, то вершина С совместится с вершиной С1, при этом совместятся лучи ВС и В1С1, АС и А1С1(рис.2).Так как ВС = В1С1, вершина В совместится с вершиной В1(рис.3). Но нам неизвестно равен ли угол В углу В1, нельзя утверждать что, вершина А совпадёт с вершиной А1, значит нельзя сказать, что треугольники равны. Значит теорема не верна.   В(В1) В В В1 А(А1) С(С1) А(А1) С(С1)Рисунок № 2 Рисунок № 3 Второй случай. Формулировка: Если две стороны и угол, лежащий против большей из них одного треугольника соответственно равны двум сторонам и углу, лежащему против большей из них другого треугольника, то такие треугольники равны.      В В1 Дано: АВС, А1В1С1, АВ = А1В1, ВС = В1С1, А = А1. Доказать: АВС = А1В1С1.А С А1 С1 Доказательство: П  усть у треугольников АВС и А1В1С1, АВ = А1В1, ВС = В1С1, А = А1, попробуем показать, что треугольники равны.Т ак как А = А1, то вершина А совместится с вершиной А1, при этом совместятся лучи АС и А1С1, АВ и А1В1(рис.4). Так как АВ = А1В1, вершина В совместится с вершиной В1(рис.5). Так как ВС = В1С1, то вершина С совместится с вершиной С1(рис.6). Следовательно, АВС = А1В 1С1. Значит теорема верна.В В(В1) В(В1)   В1А(А1) С1 С А(А1) С1 С А(А1) С(С1) Рисунок № 4 Рисунок № 5 Рисунок № 6 Таким образом, можно считать эту теорему ещё одним признаком равенства треугольников. Третья теорема. Формулировка: если два угла и сторона прилежащая к одному из них одного треугольника соответственно равны двум углам и стороне прилежащей к одному из них другого треугольника, то такие треугольники равны.     В В1 Дано: АВС, А¹В¹С¹, АВ = А1В1, А = А1, С = С1. Доказать: АВС = А1В1С1.А С А1 С1 Д оказательство:Пусть у треугольников АВС и А1В1С1, АВ = А1В1, А = А1, С = С1, попробуем доказать, что треугольники равны. Т  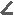ак как у треугольников АВС и А1В1С1 два угла равны: А= А1, С= С1;То третий угол будет равен по свойству углов треугольника. Таким образом, треугольники АВС и А1В1С1, будут равны по второму признаку: два угла и сторона, заключённая между ними. Из всего вышесказанного мы сделали вывод, что это не отдельный признак равенства треугольников, а частный случай второго признака. Вывод: В ходе исследования мы обнаружили ещё один признак равенства треугольников. А именно по двум сторонам и углу лежащему против большей из них. Рекомендации: Мы предлагаем рассматривать этот признак при обучении учащихся в седьмом классе. Так же данный признак можно использовать в отраслях промышленности, где при изготовлении планов и чертежей необходимо знать признаки равенства треугольников. Список литературы:
|