Функция y = x 2 и её график
 Скачать 114.92 Kb. Скачать 114.92 Kb.
|
  Муниципальное бюджетное общеобразовательное учреждение Муниципальное бюджетное общеобразовательное учреждение«Самосдельская средняя общеобразовательная школа имени Шитова В.А.» Урок алгебры в 7 классе на тему «Функция y = x2 и её график » Разработала: учитель математики ЯКОВЛЕВА Л. В. 2011 – 2012 учебный год Тема урока: Функция y = x2 и её график. Цели урока: ввести определение функции y = x2; изучить её свойства; научить строить и читать график этой функции; показать прикладной характер изучаемого материала; научить решать уравнения графическим способом; развивать навыки исследовательской работы; графическую культуру учащихся; воспитывать целенаправленное отношение к деятельности, аккуратность, наблюдательность, интерес к окружающим явлениям. Тип урока: урок изучения нового материала с использованием ИКТ. Оборудование: компьютер, проектор, экран, компьютерные презентации; бланки математического исследования; тексты самостоятельной работы. Ход урока. 1.Организация начала урока. Презентация «Функция y = x2 и её график». Слайды 1 – 2. ● Сообщение темы и цели урока. 2. Актуализация опорных знаний. Слайды 3 – 6. Устные упражнения. ● Назовите координаты точек, симметричных точкам (2; 6); (-1; 4); (0; 0); (-3; -5) относительно оси y. ● Найдите значения функции y = 5x + 4, если х = - 1; - 2; 3; 5. ● Укажите область определения функции: y = 16 – 5x; y =  y = y =  y = y = 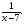 Повторение теоретических сведений. ● Расшифруйте предложенные термины. Зависимость между двумя переменными, при которой Функция каждому значению независимой переменной соответствует единственное значение зависимой переменной. Аргумент Независимая переменная, значения которой выбирают произвольно. График функции Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. Область определения. Все значения, которые принимает независимая переменная. Линейная функция. Функция, заданная формулой вида y = kx + b, где х – переменная, k и b некоторые числа. 3. Изучение нового материала. Слайд 7. ● Итак, мы уже знаем, что функция или функциональная зависимость – это зависимость между двумя переменными, при которой каждому значению одной переменной соответствует единственное значение другой переменной. Как известно, всякая функция описывает процессы движения и изменения, происходящие в окружающем нас мире. ● Рассмотрим, например, зависимость площади квадрата от его стороны. - Что будет происходить с площадью квадрата, если мы будем изменять длину его стороны? - Сторону квадрата увеличили в 3 раза. Как измениться его площадь? - А если сторону уменьшить в 4 раза, что произойдёт тогда? - Какой формулой задаётся зависимость площади квадрата от его стороны?. (S = a2) - Будет ли зависимость площади квадрата от его стороны являться функцией? Объясните ответ. ● Если в формуле S = a2 площадь обозначить через y, а длину стороны через х, то рассмотренная нами функции задаётся формулой вида y = x2, которую называют квадратичной. Слайды 8 – 10. ● По словам французского писателя Оноре де Бальзака «Ключом ко всякой науке является вопросительный знак». Поэтому мы сейчас проведём небольшое математическое исследование и попытаемся ответить на вопросы: что представляет собой функция y = x2?; какими свойствами она обладает?; как выглядит её график? Все результаты исследований вы будете заносить в протокол исследования. (У каждого ребёнка на парте специальный бланк). (Приложение). ● Работу начнём с того, что составим таблицу соответственных значений x и y рассматриваемой нами функции. (Задание №1 математического исследования). Дети самостоятельно заполняют таблицу, можно использовать таблицу квадратов двузначных чисел.
● Проверьте ваши результаты. (Правильные ответы на слайде). ● Выполним Задание №2. Построим график функции. По данным таблицы учащиеся строят график функции, учитель оказывает необходимую помощь «слабым» детям. ● Давайте посмотрим, что у нас получилось. (Изображение графика на слайде). ● Итак, мы построили кривую, которая является графиком функции y = x2. Ясно, что этот график неограниченно продолжается вверх, справа и слева от оси y. Обратите внимание, ребята, на вид графика вблизи начала координат. Для значений х, близких к нулю, график практически сливается с прямой Ох. В таком случае говорят, что кривая касается оси абсцисс. ● График функции y = x2 называют параболой. Откуда взялось это название и что оно означает? Презентация «Многоликая парабола». Историческая справка. Древнегреческий математик Аполлоний Пергский где – то за 200 лет до нашей эры разрезав конус, линию среза назвал параболой, что в переводе с греческого означает «приложение» или «притча», о чём математик и написал в восьмитомнике «Конические сечения». И долгое время параболой называли лишь линию среза конуса, пока не появилась квадратичная функция. ● Параболу часто можно встретить на практике. Знаете ли вы, что: Траектория камня, брошенного под углом к горизонту, летящего футбольного или баскетбольного мяча, артиллерийского снаряда является параболой (при отсутствии сопротивления воздуха). То есть всё, что мы бросим под углом к горизонту, будет лететь по параболе, поскольку движение под действием гравитации подчиняется законам квадратичной функции. Струйки воды фонтана также описывают траекторию в виде параболы. Форму параболы принимают орбиты комет, спутников и космических кораблей. Парабола обладает оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы (определённой точке), отражаются параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, а также параболических антенн. ● Многоликую параболу можно встретить и в природе. Невероятно, но факт! Например, перевал в горном районе Ергаки (Саяны, Сибирь) напоминает по форме параболу. Он так и называется перевал Парабола. Или вот это дерево! Презентация «Функция y = x2 и её график». Слайды 11 – 15. ● Продолжим наше исследование. Наша задача выяснить, какими свойствами обладает функция y = x2 и как эти свойства отражаются на её графике. Для этого выполните Задание №4. Опираясь на таблицу значений и график функции, учащиеся заполняют таблицу в бланке исследования, получая при этом свойства функции и отражение этих свойств на графике. Учитель контролирует работу и оказывает необходимую помощь. ● Обсудим свойства функции y = x2. Учащиеся формулируют свойства, а учитель, с помощью детей, комментирует их и делает необходимые дополнения, используя слайды. - Область определения функции D(f): любое число. Действительно, любое число х можно возвести во вторую степень. - Если х = 0, то y = 0. График функции, следовательно, проходит через начало координат. - Если х ≠ 0, то y > 0. Действительно, квадрат любого числа, отличного от нуля, есть число положительное. Значит, все точки графика функции, кроме точки (0; 0), лежат выше оси х, т. е. в I и II координатных четвертях. - Исходя из того, что функция принимает только неотрицательные значения, т. е. y ≥ 0, можно сделать вывод, что область значений функции E(f): все значения y ≥ 0, . т. е. неотрицательные. - Противоположным значениям х соответствует одно и то же значение y. Это следует из того, что (- х)2 = х2 при любом х. Например, (-3)2 = 32 = 9. Таким образом, точки графика, имеющие противоположные абсциссы, симметричны относительно оси y. Говорят, график функции симметричен относительно оси y. Заметим, что такие функции называются чётными. Слайды 16. ● Ещё раз вернёмся к параболе и перечислим её геометрические свойства: Геометрические свойства параболы. - Обладает симметрий. Осью симметрии является ось ординат. - Ось разрезает параболу на две части, которые называют ветвями параболы. - Точка (0; 0), в которой смыкаются ветви, называется вершиной параболы. - Парабола касается оси абсцисс. 4. Закрепление изученного материала. ● Русский писатель Л. Н. Толстой сказал: «Знание – орудие, а не цель». Давайте учиться использовать полученные вами сегодня знания как орудие для выполнения заданий различного характера. Слайды 17 – 18. ● Начнём с элементарного. Выполняя упражнения, учащиеся должны опираться на свойства функции и графика. ● Используя график функции y = x2 (рис. 61 учебника), найдём: а) значение функции, соответствующее значению аргумента, равному: 1,4; - 1,4; - 2,6; 3,1; - 3,1; Учитывая симметрию графика относительно оси ординат достаточно определить значения y для неотрицательных значений х. б) значения аргумента, при котором значение функции равно 4; 6; Достаточно найти одно из значений, а другое значение будет ему противоположным. в) несколько значений х, при которых значения функции меньше 4; больше 4. ● Выполните задание №1 Самостоятельной работы. (Приложение). Слайд 19. ● Вспомните, как устанавливается принадлежность точки графику заданной функции? ● Определим, принадлежит ли графику функции y = x2 точка: а) P(-18; 324); б) R(- 99; - 9081); в) S(17; 279). а) Точка P лежит во II координатной четверти, поэтому она может принадлежать графику. Подставляя координаты точки P в формулу, получим 324 = (-18)2; 324 = 324 – верное равенство. Точка P принадлежит графику функции. б) Точка R лежит в IV координатной четверти, значит, она не может принадлежать графику, поскольку все точки графика функции y = x2 лежат в верхней полуплоскости, т. е. в I и II координатных четвертях. в) Точка S лежит в I координатной четверти, она может принадлежать графику функции. Подставляя координаты точки в формулу, получим 279 = 172; 279 = 289 – неверное равенство. Точка S не принадлежит графику. ● Определите, не выполняя вычислений, какие из точек не принадлежат графику функции y = x2. Ответ объясните. (Упражнение выполняется устно). (-1; 1); (-2; -4); (0; 8); (3; -9); (1,8; 3,24); (16; 0). ● При каких значениях a точка P(a; 64) принадлежит графику функции y = x2. (Упражнение №492 учебника). ● Выполните задание №2 Самостоятельной работы. (Приложение). Слайд 20. ● С помощью графиков функций можно найти приближённые значения корней некоторых уравнений, т. е. решить уравнение графическим способом. Разберём на примерах данный способ решения. Решим графическим способом уравнения: а) х2 = 5; б) х2 = - 1; в) х2 = х + 1. Объяснение ведётся согласно учебнику (Пример 1). ● Следовательно, алгоритм решения уравнения графическим способом состоит в следующем: 1. Построить в одной системе координат графики функций, стоящих в левой и правой части уравнения. 2. Найти абсциссы точек пересечения графиков. Это и будут корни уравнения. Если точек пересечения нет, значит, уравнение не имеет корней. ● Выполните задание №3 Самостоятельной работы. (Приложение). 5. Контрольные вопросы. ● Как называется график функции y = x2? ● Как на координатной плоскости расположен график функции y = x2? ● Какова область определения функции y = x2? 6. Подведение итогов урока. Слайд 21 . 7. Домашнее задание. ● Изучить п.23. ● Выполнить упражнения №484; №486; №487; №494(а). Слайд 22. 8. Удачи вам! Презентации к данному уроку можно найти по следующей ссылке: https://nsportal.ru/shkola/algebra/library/uchebnaya-prezentatsiya-k-uroku-algebry-v-7-klasse-funktsiya-kh-v-kvadrate-i- 9. Информационные источники. Литература. 1. Алгебра. 7 класс: учебник для общеобразовательных учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова; под редакцией С. А. Теляковского. – 19-е изд. – М: Просвещение, 2010. 2. Алгебра. Дидактические материалы. 7 класс./ Л. И. Звавич, Л. В. Кузнецова, С. Б. Суворова. – 15-е изд. М: Просвещение, 2010. 3. Изучение алгебры в 7—9 классах. / Ю. Н. Макарычев, Н. Г. Миндюк, С. Б. Суворова.— М.: Просвещение, 2005—2008. 4. Рурукин А. Н., Лупенко Г. В. , Масленникова И. А. Поурочные разработки по алгебре: 7 класс М: ВАКО, 2006. 5. Энциклопедический словарь юного математика. 6. Алгебра: Рабочая тетрадь для 7 класса./Миндюк М. Б., Миндюк Н. Г. – М: Издательский Дом «ГЕНЖЕР», 1998. Интернет – ресурсы. 1.https://liveinternet.ru/community/geo_club/post117553794/ 2. https://ru.wikipedia.org/wiki/%D0%A4%D0%B0%D0%B9%D0%BB:ParabolicWaterTrajectory.jpg 3. https://upload.wikimedia.org/wikipedia/commons/thumb/3/36/LaPedreraParabola.jpg/400px-LaPedreraParabola.jpg |