|
геометрическая прогрессия q= b
Уровень сложности
|
Задание
|
Ответы
| А |
1 Дано (bn)- геометрическая прогрессия q=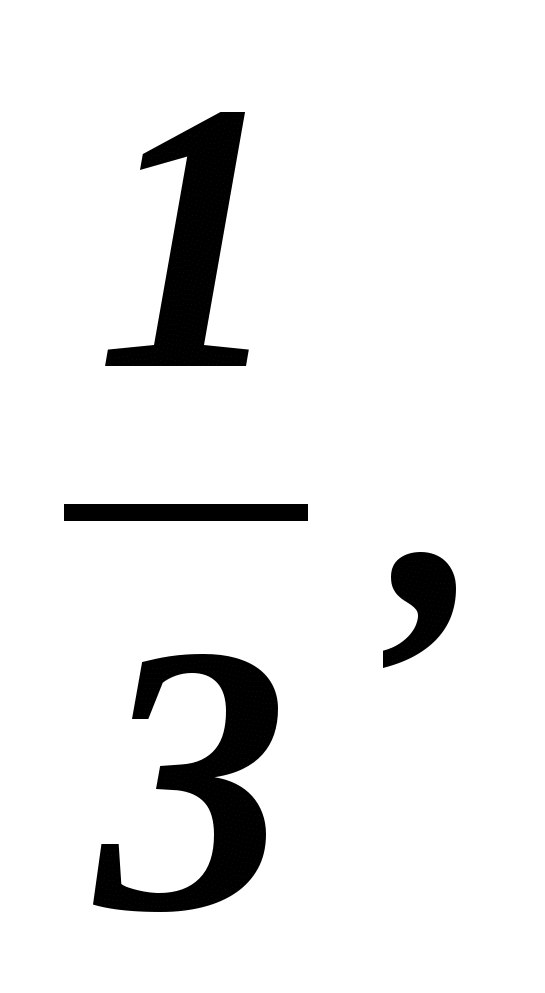 b1=24.3. Найти: b3, b7, b10 b1=24.3. Найти: b3, b7, b10
|
2,7;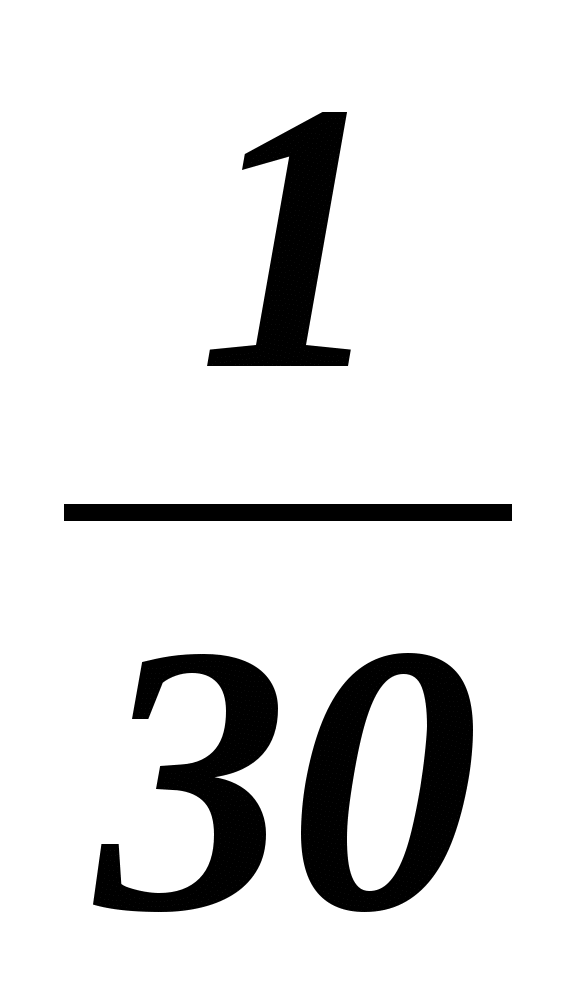 ; ;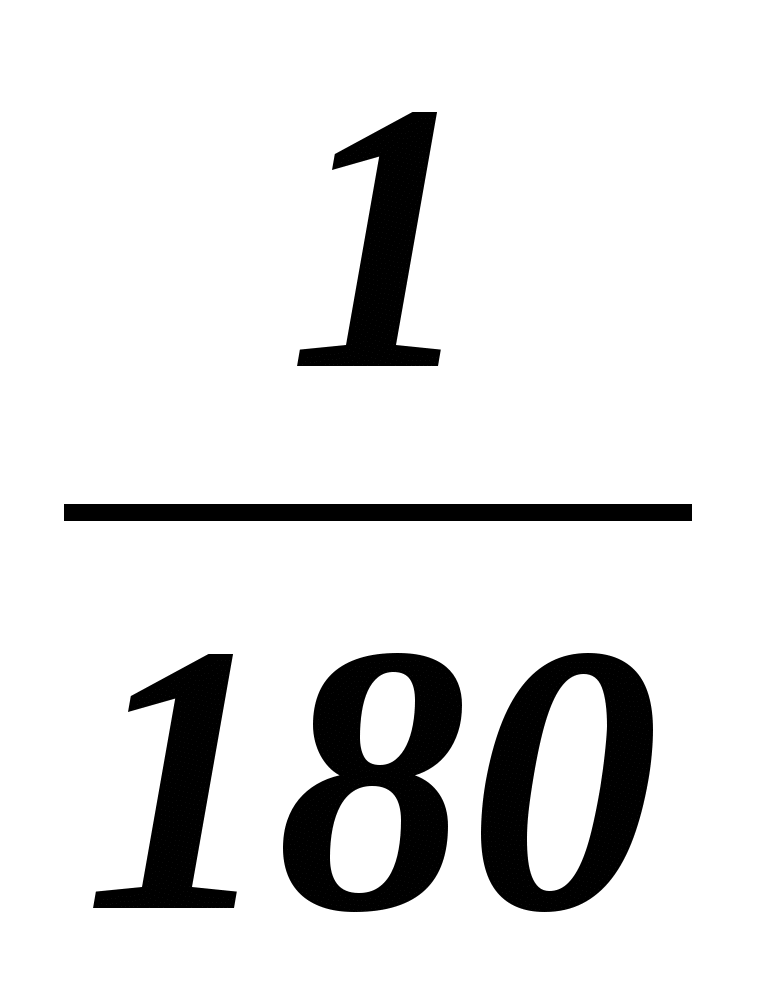
|
|
2. В геометрической прогрессии (bn) найти q, если b1=729, b8=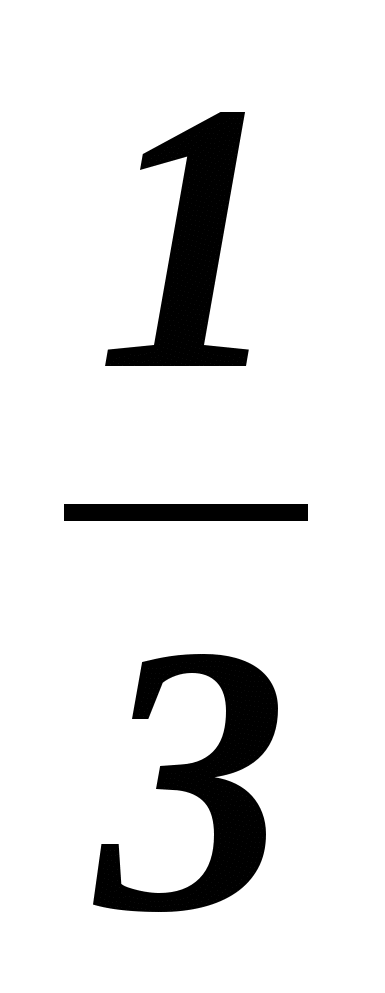
|
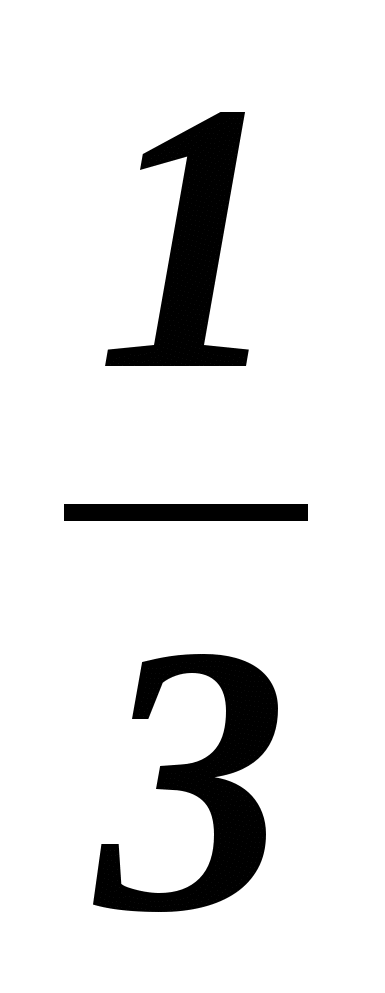
|
|
3.Найти знаменатель геометрической прогрессии, если сумма первых трех ее членов равна 21, а третий член равен 12.
|
2; -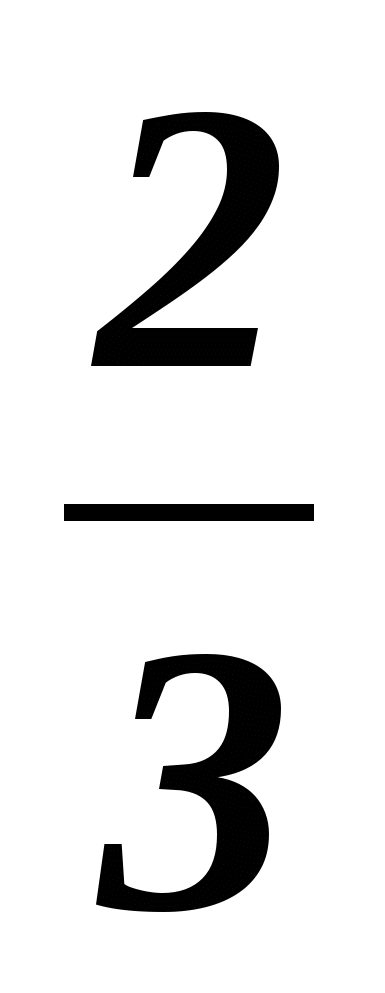
|
|
4. Между числами 9 и 243 поставить пять чисел так, чтобы
получилась геометрическая прогрессия.
|
9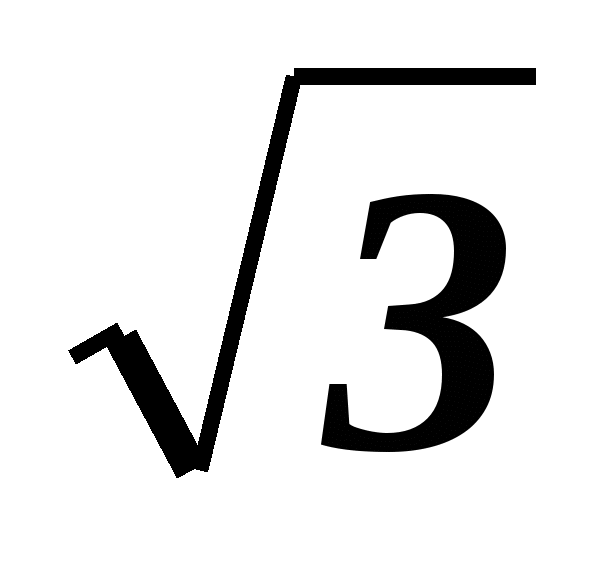 ; 27; 27 ; 27; 27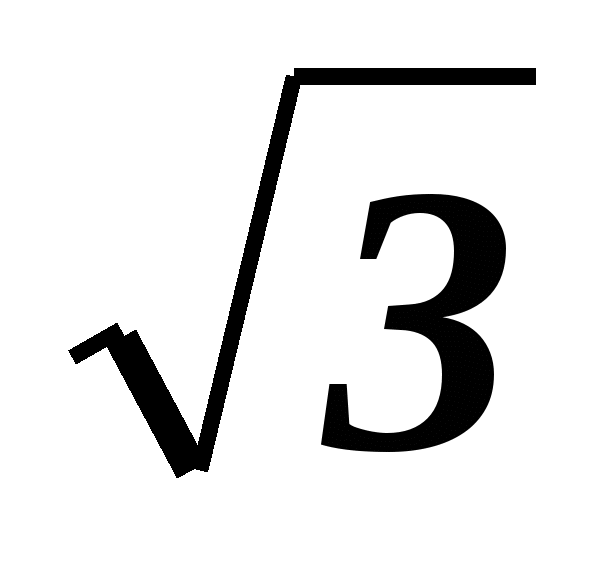 ; 8; 81 ; 8; 81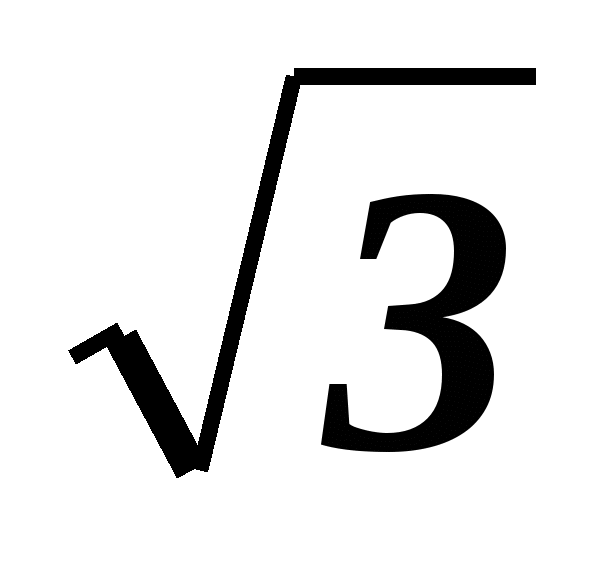
|
|
5.Найти 1995-ый член геометрической прогрессии, если 1959-ый и 1977-й ее член равен соответственно 4 и 1.
|
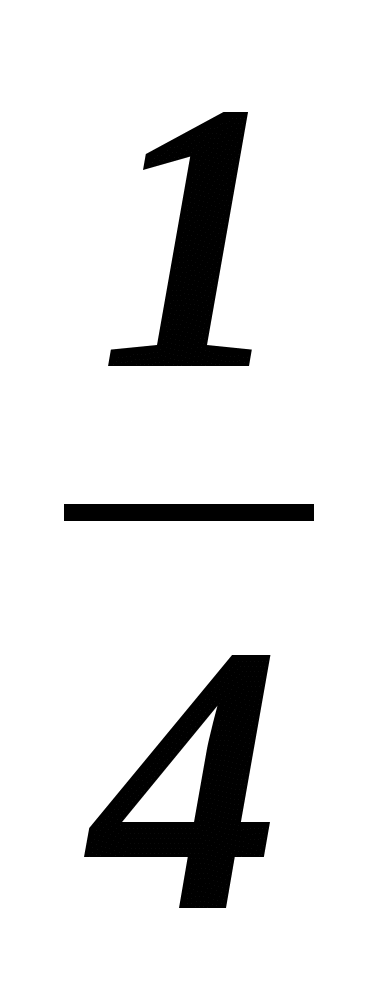
|
|
6. Найти знаменатель убывающей геометрической прогрессии, если сумма первого и четвертого членов равна 27, а произведение второго и третьего членов равно 72.
|
0,5
|
|
7. Сумма первых трех членов геометрической прогрессии равна
(-49), а сумма следующих трех равна 392. Найти сумму первых пяти членов .
|
-179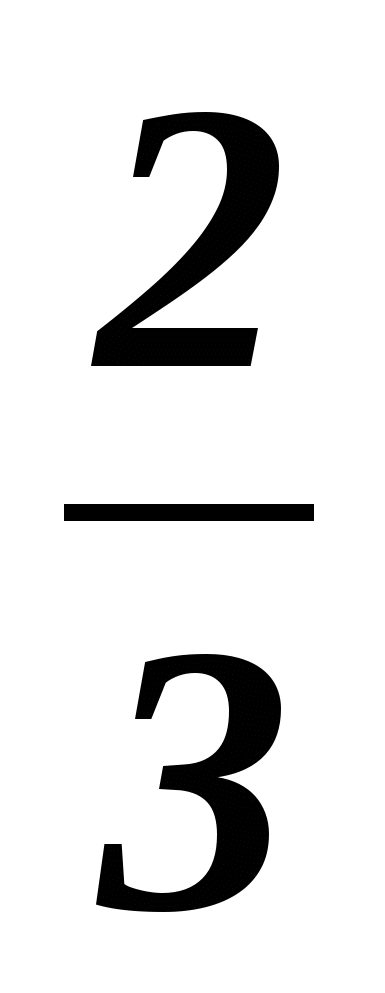
|
|
8.Найти три числа, зная, что они образуют возрастающую геометрическую прогрессию и их сумма равна 14, а сумма их квадратов равна 84.
|
2; 4; 8.
| В |
9. Найти пятый член геометрической прогрессии, у которой сумма первых трех членов равна 7, а произведение этих членов равно 8.
|
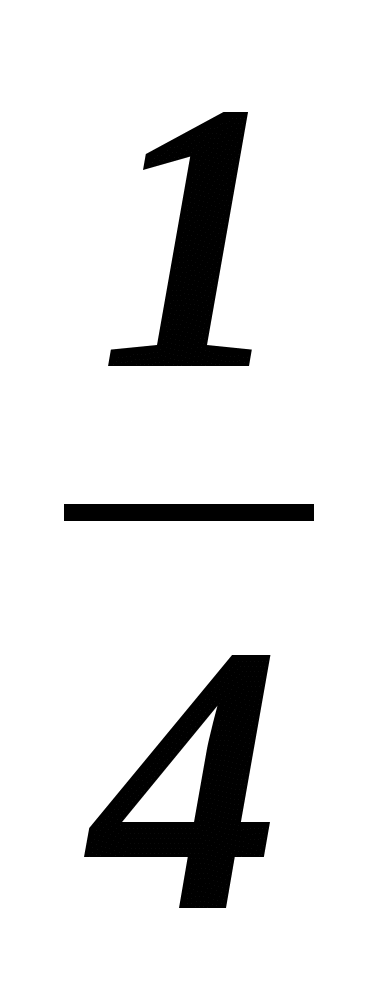 или 16 или 16
|
|
10.Найти три числа, образующих геометрическую прогрессию, таких, что их сумма равна 21, а сумма обратных величин равна 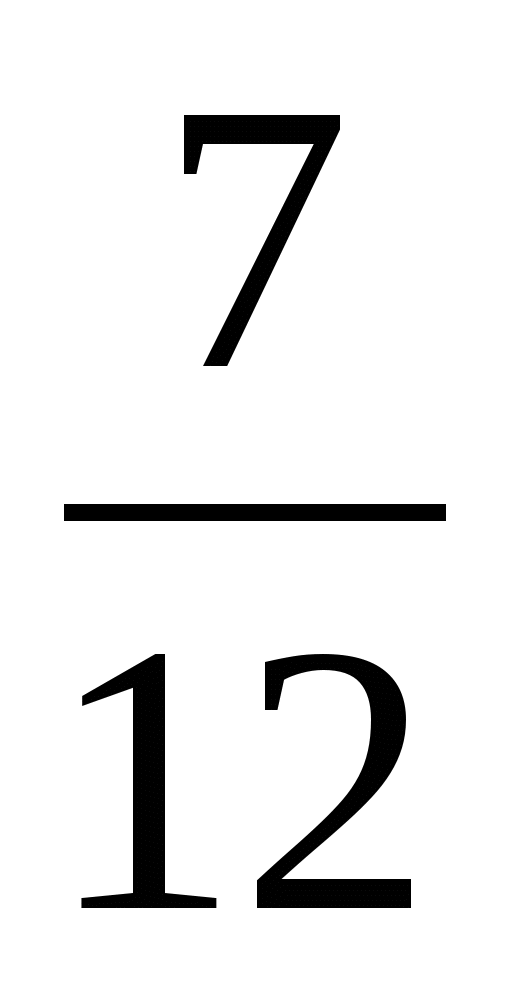
|
3; 6; 12 или 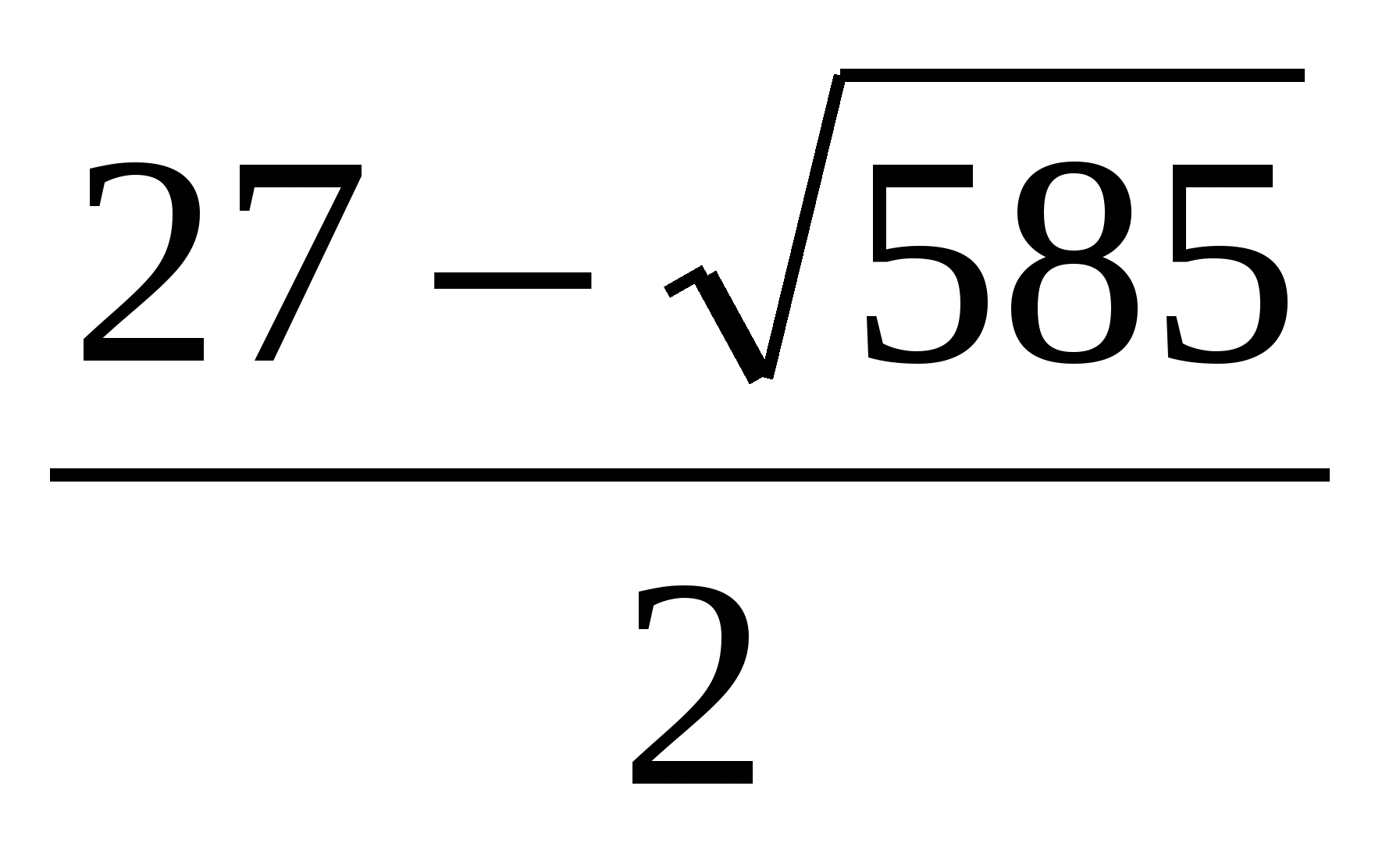 ; - 6 ; - 6 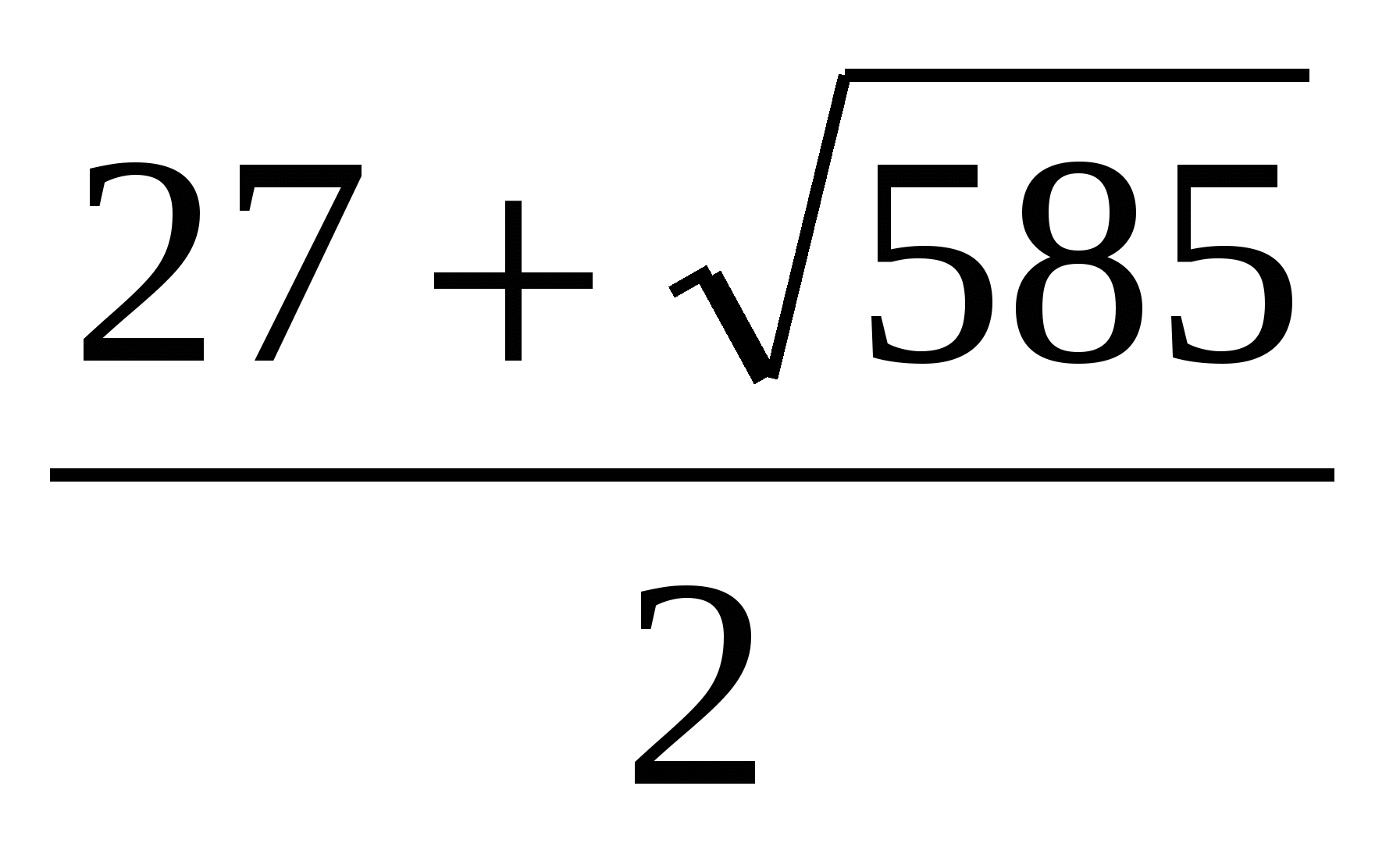 или эти тройки чисел в обратном порядке или эти тройки чисел в обратном порядке
|
|
11.Число членов геометрической прогрессии четно. Сумма всех ее членов в три раза больше суммы членов, стоящих на нечетных местах. Найти знаменатель геометрической прогрессии
.
|
2
|
|
12. В геометрической прогрессии четное число членов.
Найти знаменатель прогрессии, если известно, что сумма ее членов с нечетными номерами составляет 10% от суммы всех членов.
|
9
|
|
13. Сумма любых пяти последовательных членов геометрической прогрессии в 19 раз больше, третьего из них. Найти шестой член прогрессии, если ее десятый член равен 1.
|
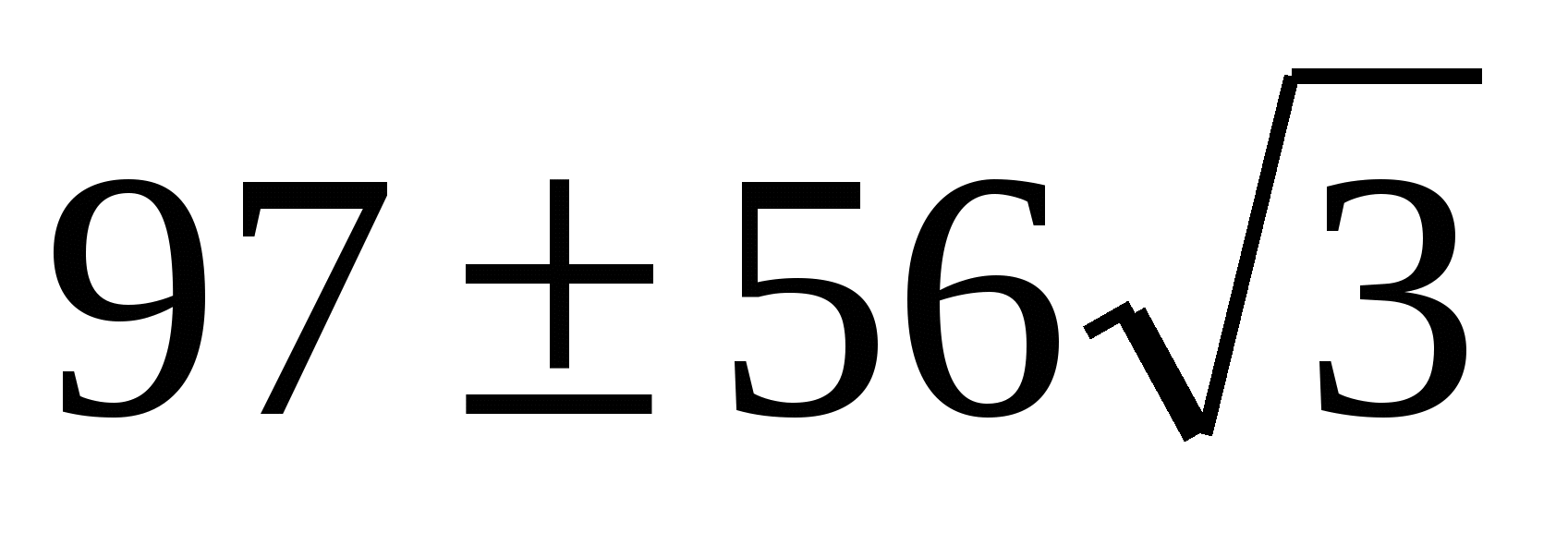 ; ; 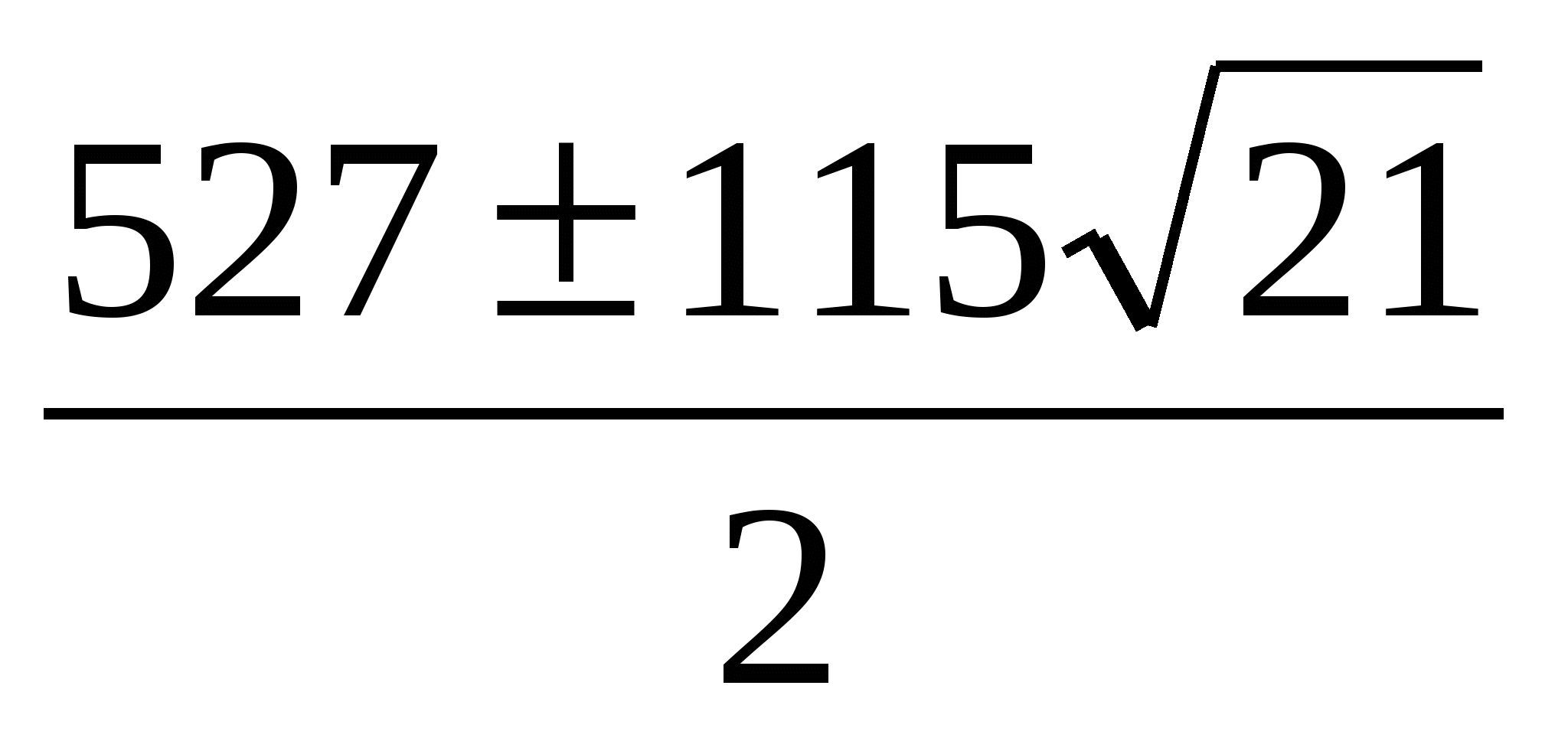
| Практикум №32
по теме «Геометрическая прогрессия»
|
14.Сумма бесконечно убывающей геометрической прогрессии равна 21, а ее первый член равен 7. Найти сумму первых трех членов этой прогрессии.
|
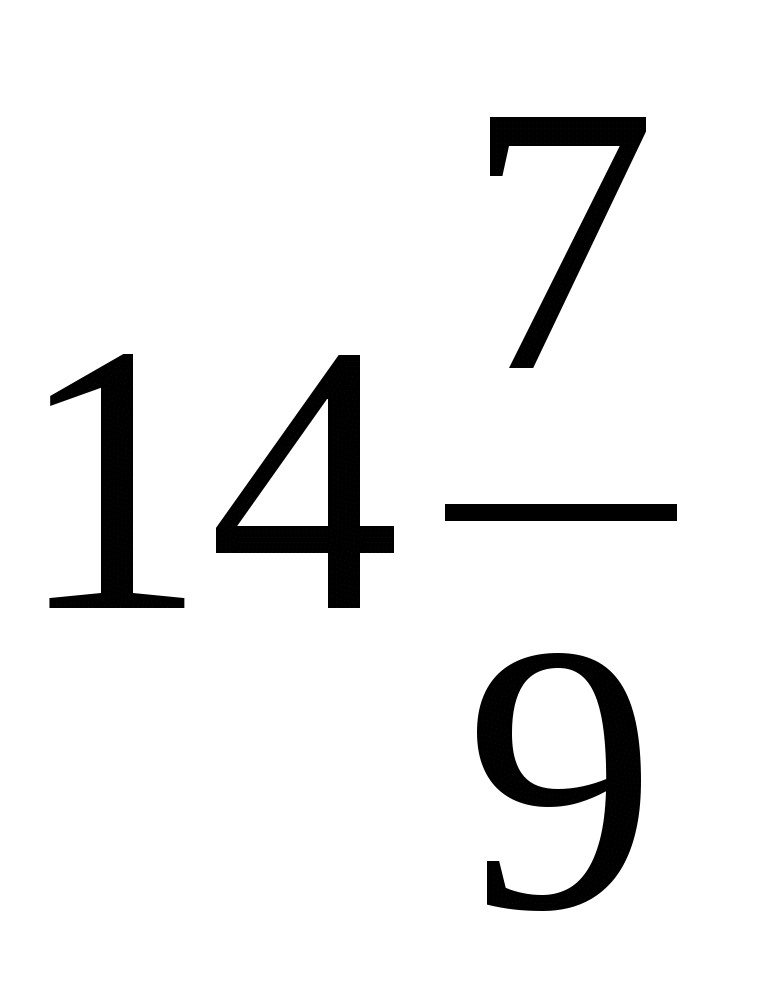
|
|
15. Сумма бесконечно убывающей геометрической прогрессии равна 4, а сумма кубов ее членов равна 192. Найти первый член и знаменатель прогрессии
|
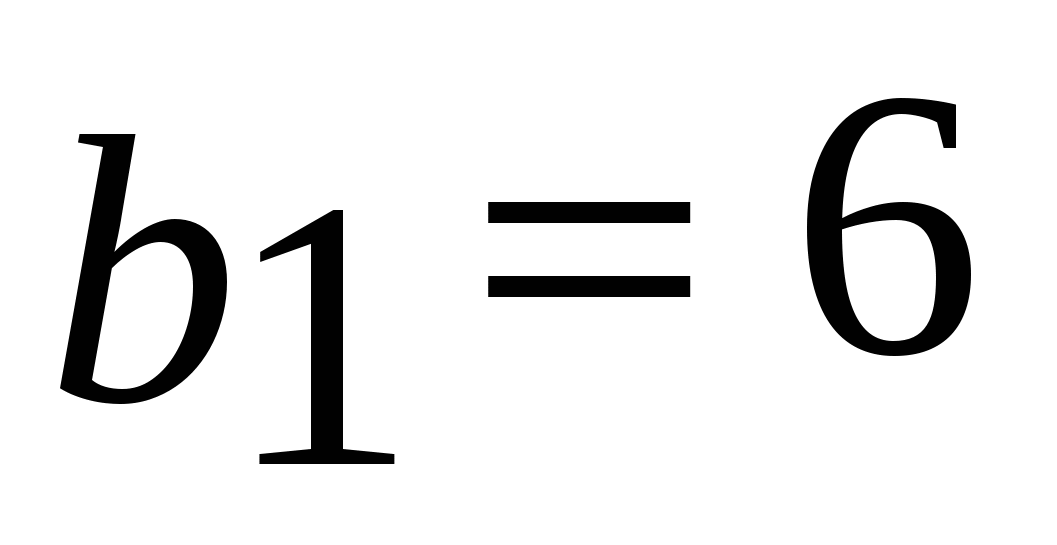 , , 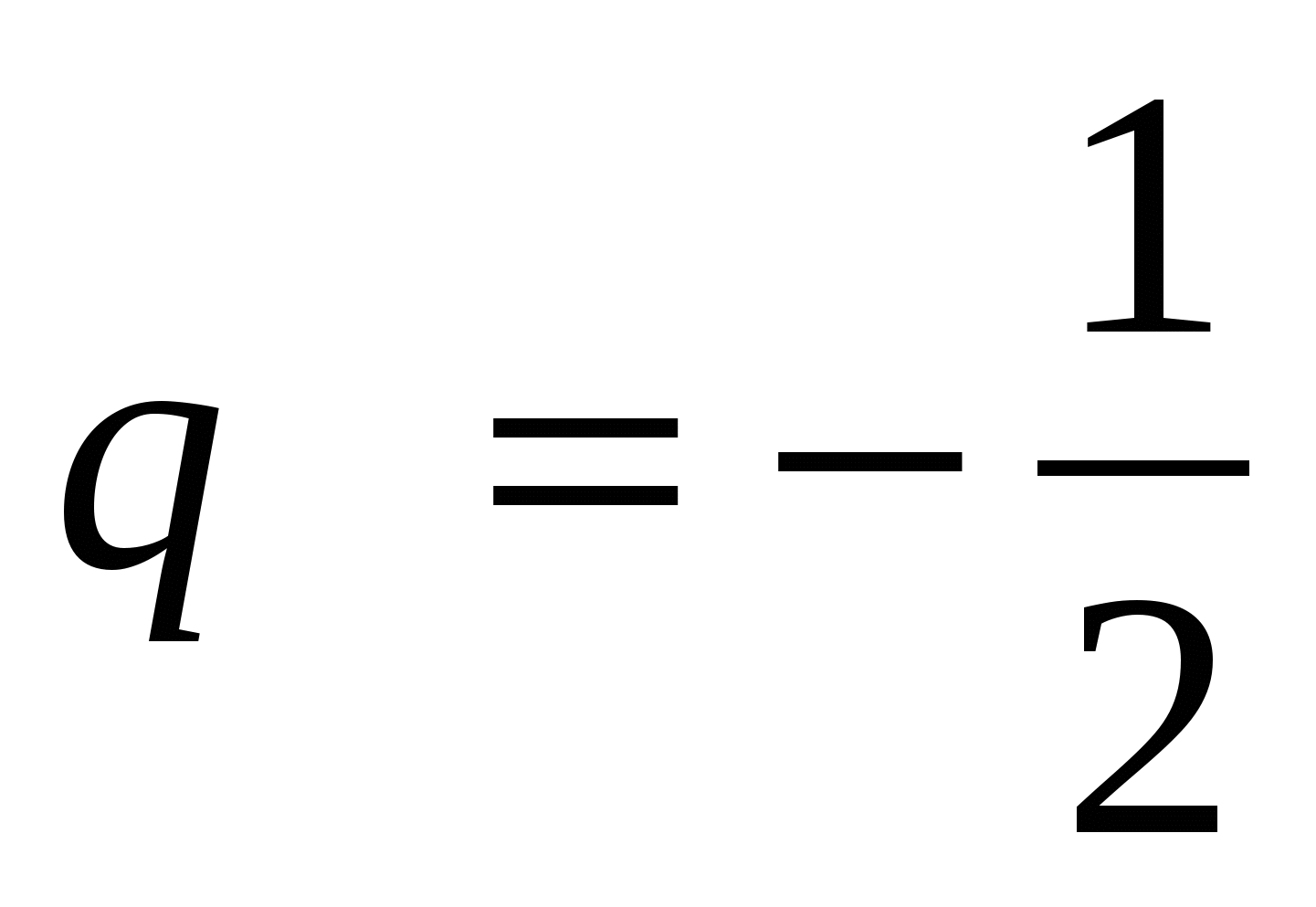
| | |
16.Найти три числа, составляющие геометрическую прогрессию, которые в сумме дают 26. Если к указанным числам прибавить соответственно 1; 6; 3, то получим три числа , образующих арифметическую прогрессию.
|
2; 6; 18 или 18; 6; 2.
|
|
17. Найти сумму членов прогрессии с пятого до десятого: 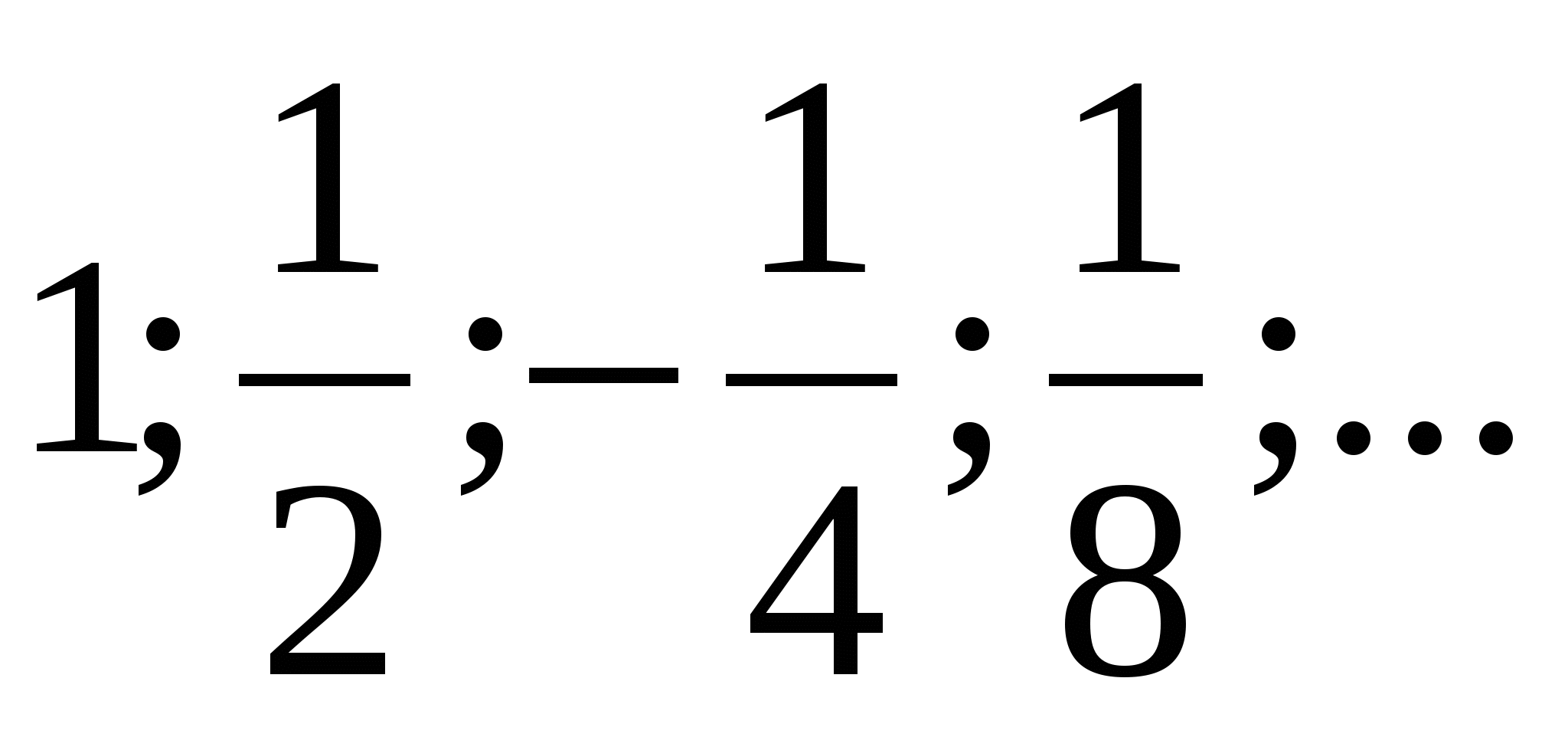
|
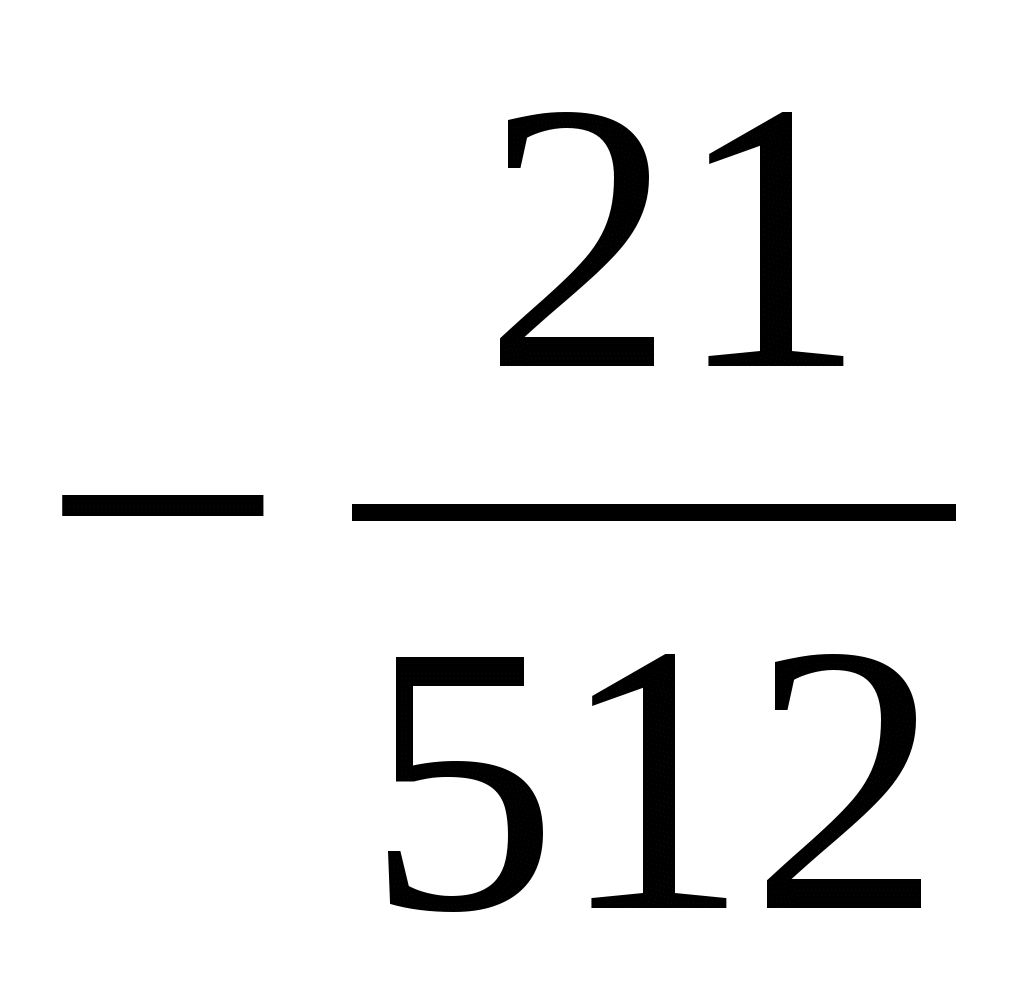
|
|
18.Сумма n первых членов геометрической прогрессии равна –341, ее первый член равен –1, а знаменатель 4. Найти n.
|
5
|
|
19. Четыре числа составляют геометрическую прогрессию, если из них вычесть соответственно 2; 1; 7; 27, то получим три числа , образующих арифметическую прогрессию. Найти эти числа.
|
7; 14; 28; 56.
|
|
20. Найти первый член бесконечно убывающей геометрической прогрессии если сумма членов этой прогрессии равна 20,4, а отношение 8-го члена к 5-ому члену равно 0,125.
|
10,2
| С |
21. При каких значениях Х являются последовательными членами некоторой геометрической прогрессии следующие три числа: а)sin2(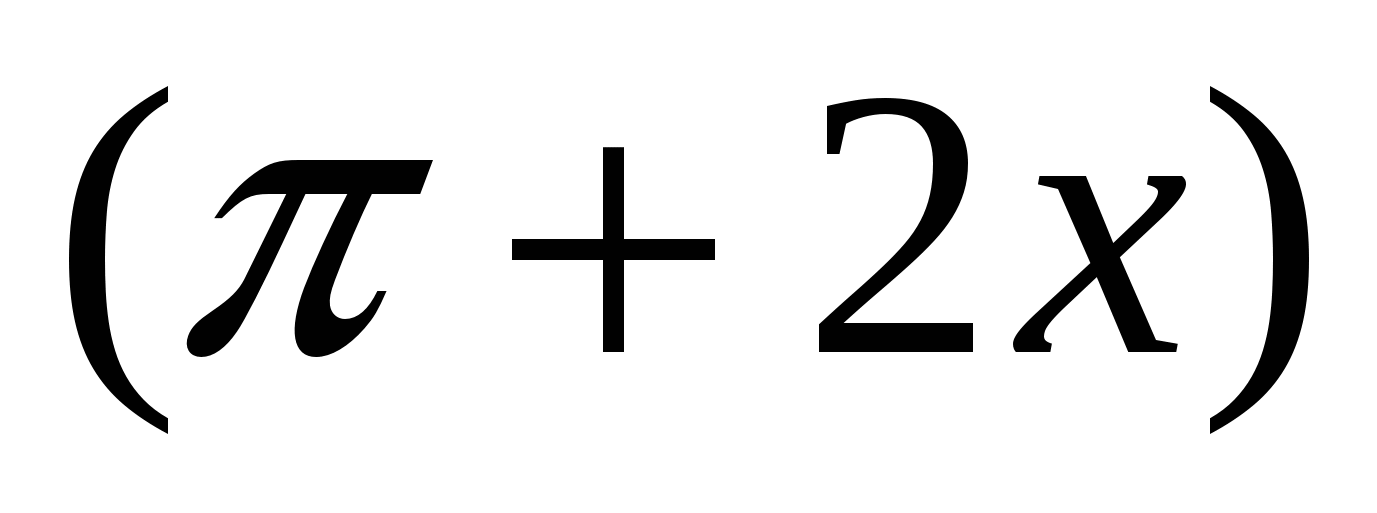 ; tg ; tg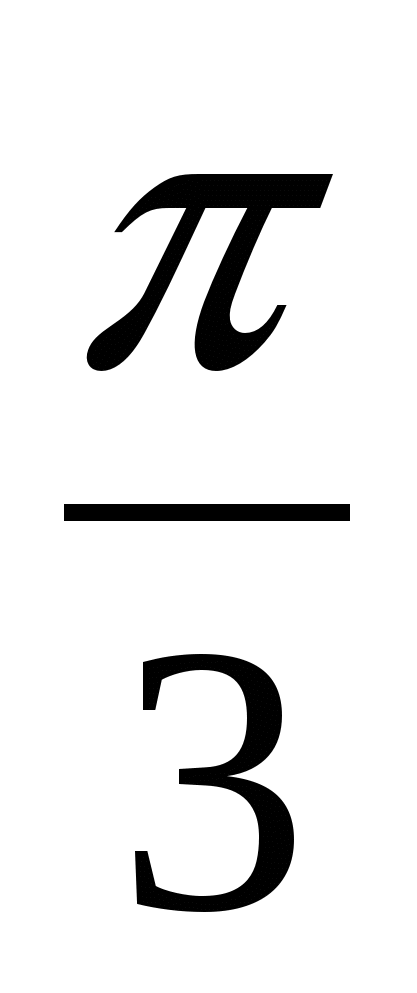 ; 12 ; 12
b)22x+1; 2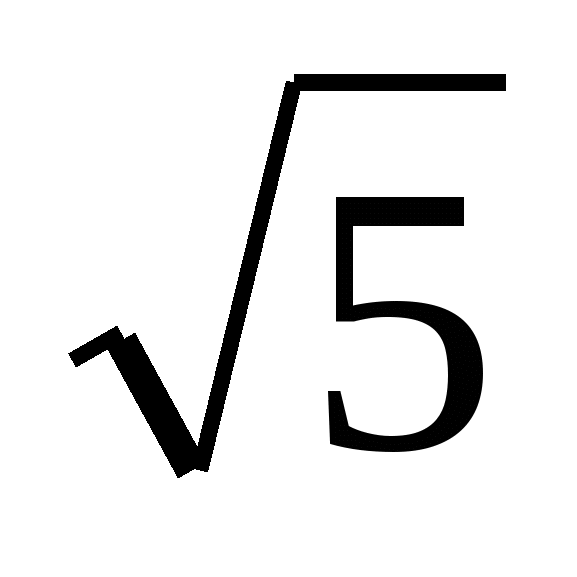 ; 1+2 ; 1+2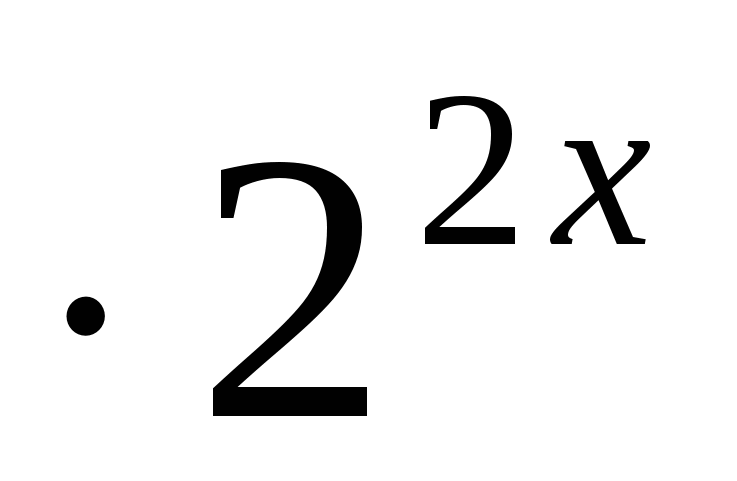
|
а) 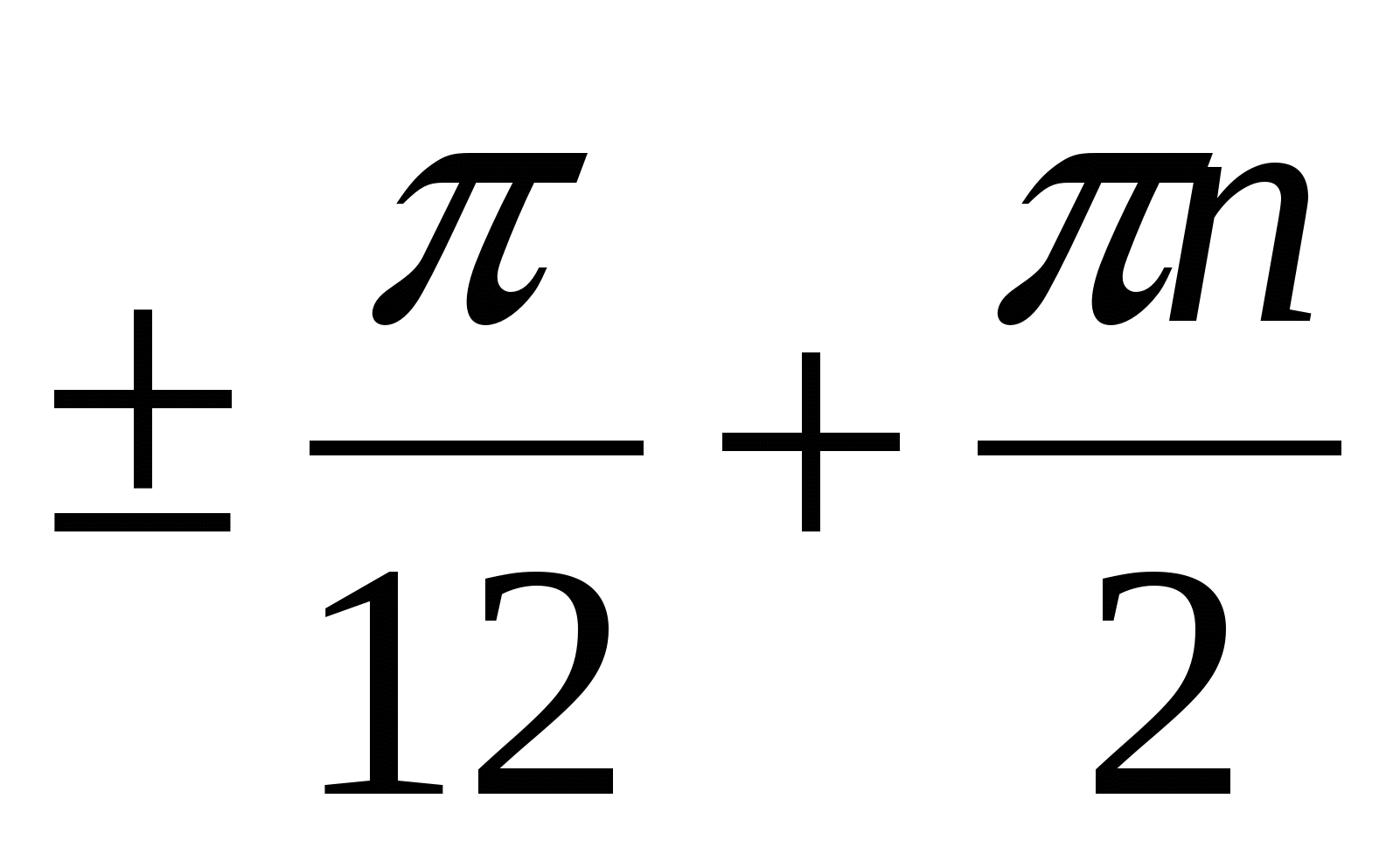 ; ; 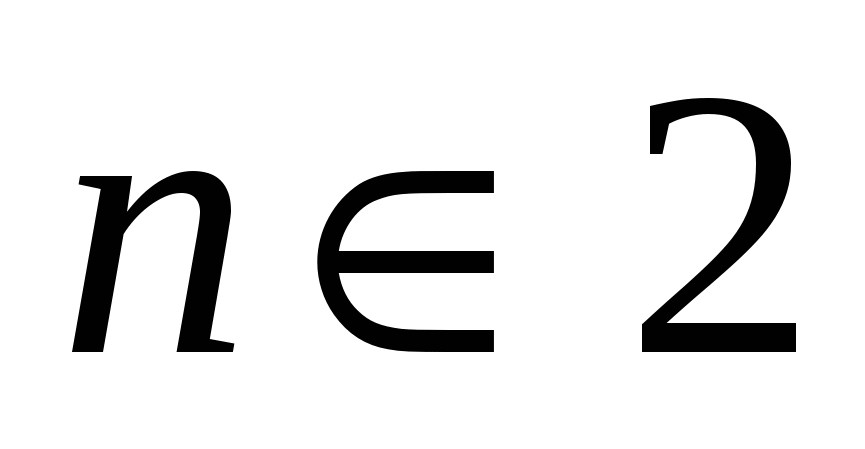
б)0,5
|
|
22.Пусть X1 и X2 корни уравнения x2-3x+A=0,а х3 и х4-корни уравнения х2-12х+В=0. Известно что x1, x2, x3, x4 (в указанном порядке) составляют возрастающую геометрическую прогрессию. Найти А и В.
|
A=2; B=32.
|
|
|
|
 Скачать 43.43 Kb.
Скачать 43.43 Kb.