Уровень сложности
|
Задачи
|
Ответы
|
A
|
1). Найти пятнадцатый член и сумму пятнадцати членов прогрессии 2; 5; 8; 11; …
|
1 44; 345
|
|
2). Найти первый член и разность арифметической прогрессии (an), если a3 = 25, a10 = -3
|
33; -4
|
|
3). Числа -100 и -78 являются соответственно седьмым и девятым членами арифметической прогрессии. Найти тринадцатый член и сумму тринадцати членов этой прогрессии.
|
-34; -1300
|
|
4). В арифметической прогрессии сумма третьего и четвертого членов равна 17, а разность между вторым и пятым членами равна -9. Найти шестой член прогрессии.
|
16
|
|
5). В арифметической прогрессии известно, что a11 + a7 = 56; a9 + a6 = 47. Найти сумму первых трех членов прогрессии.
|
21
|
|
6). Пятый член арифметической прогрессии равен 14, а восьмой ее член равен 23. Найти сумму первых пятнадцати членов прогрессии.
|
345
|
|
7). Дано: (an) – арифметическая прогрессия
a1 + a3 = 26
a1 + a4 = 30
an = 57
Найти: n
|
13
|
|
8). В арифметической прогрессии сумма второго и третьего членов равна 8, а сумма четвертого и пятого членов равна 16. Найти сто первый член прогрессии.
|
201
|
|
9). Число 125 является членом арифметической прогрессии 7; 9; 11; …Найти номер этого члена.
|
60
|
|
10) Сумма первого и пятого членов вырастающей (d > 0) арифметической прогрессии равна 14, а произведение второго и четвертого членов равна 45. Сколько членов прогрессии нужно взять, чтобы в сумме получить 24?
|
4
|
В
|
11) В арифметической прогрессии 20 членов. Сумма членов, имеющих четные номера равна 250, а сумма членов, имеющих нечетные номера равна 220. Найти прогрессию.
|
a1 = -5; d = 3
|
|
12) Найти площадь прямоугольного треугольника, периметр которого равен 12, а стороны образуют арифметическую прогрессию.
|
6
|
|
13) Сумма трех чисел, являющихся последовательными членами арифметической прогрессии, равна 2, а сумма их квадратов равна 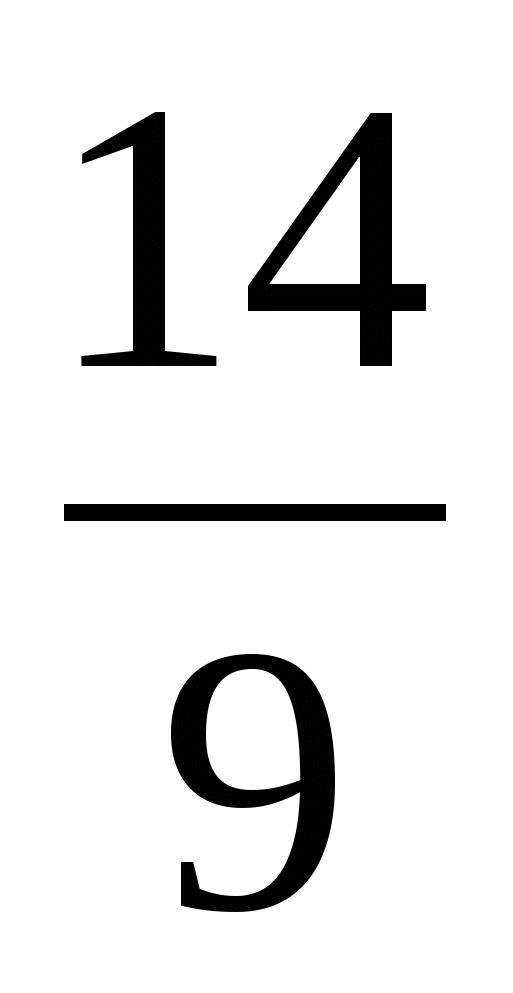 Найти эти числа. Найти эти числа.
|
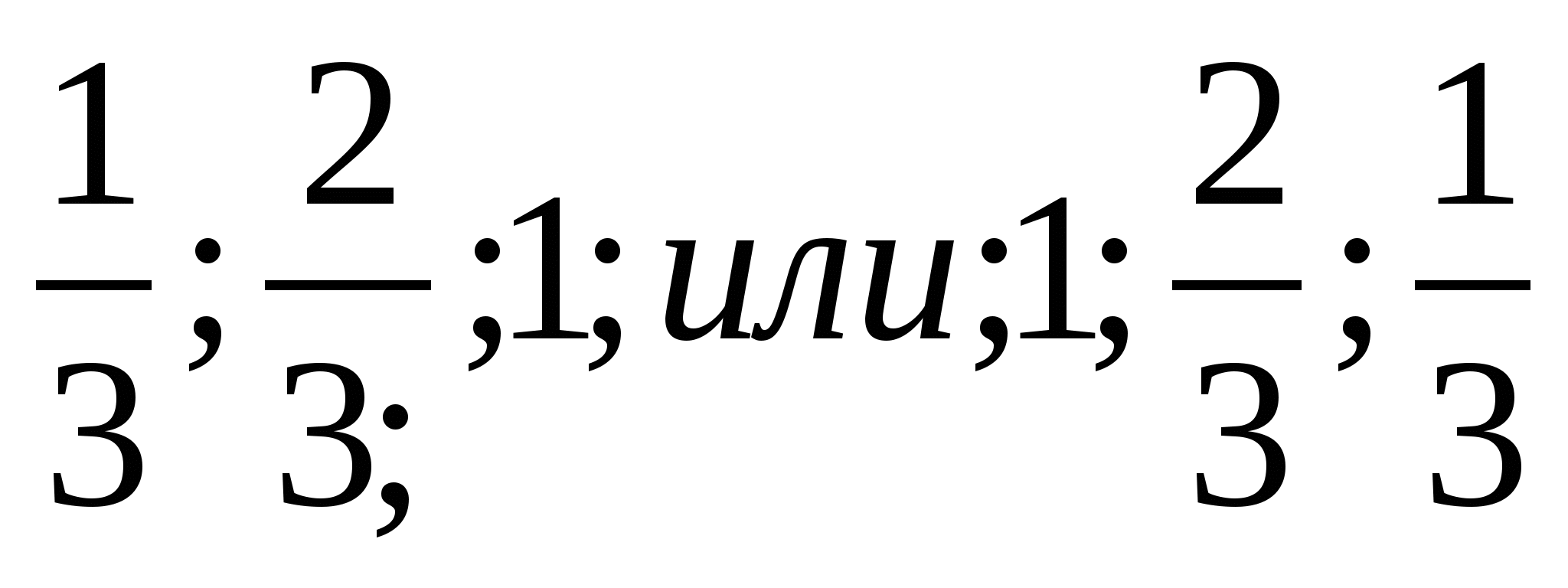
|
|
14) При каких значениях x являются четырьмя последовательными членами арифметической прогрессии числа:
1 + x ; x2 + 4; 2x + 9; 9x.
|
2
|
|
15) Найти сумму всех четных чисел k, каждое из которых делится без остатка на 33 и удовлетворяет условию -396 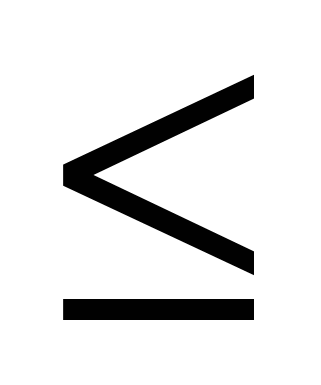 k< 265 k< 265
|
-726
|
|
16) Найти сумму всех нечетных чисел k, каждое из которых делится без остатка на 11 и удовлетворяет условию -99 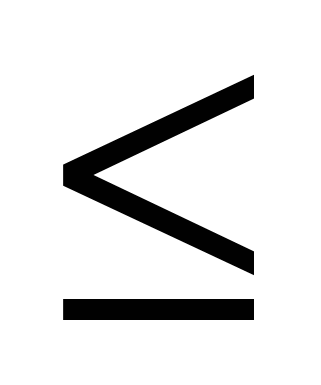 k <232 k <232
|
1056
|
|
17) Определить, при каких значениях x числа log32, log3(2x-6), log3(2x+34) образуют арифметическую прогрессию.
|
4
|
|
18) При каких значениях 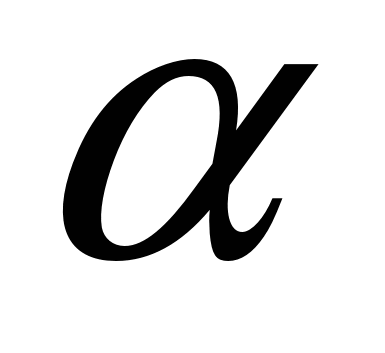 являются последовательными членами некоторой арифметической прогрессии три числа: являются последовательными членами некоторой арифметической прогрессии три числа:
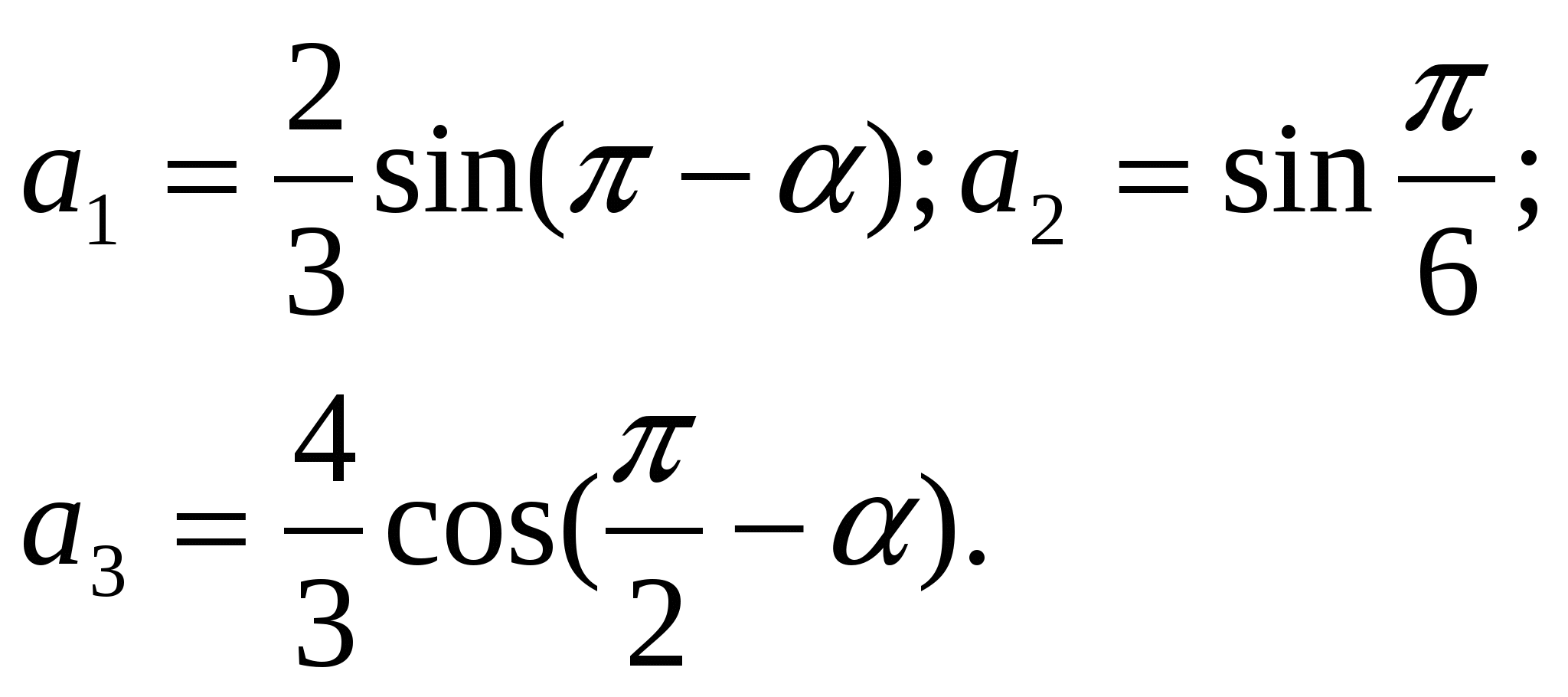
|
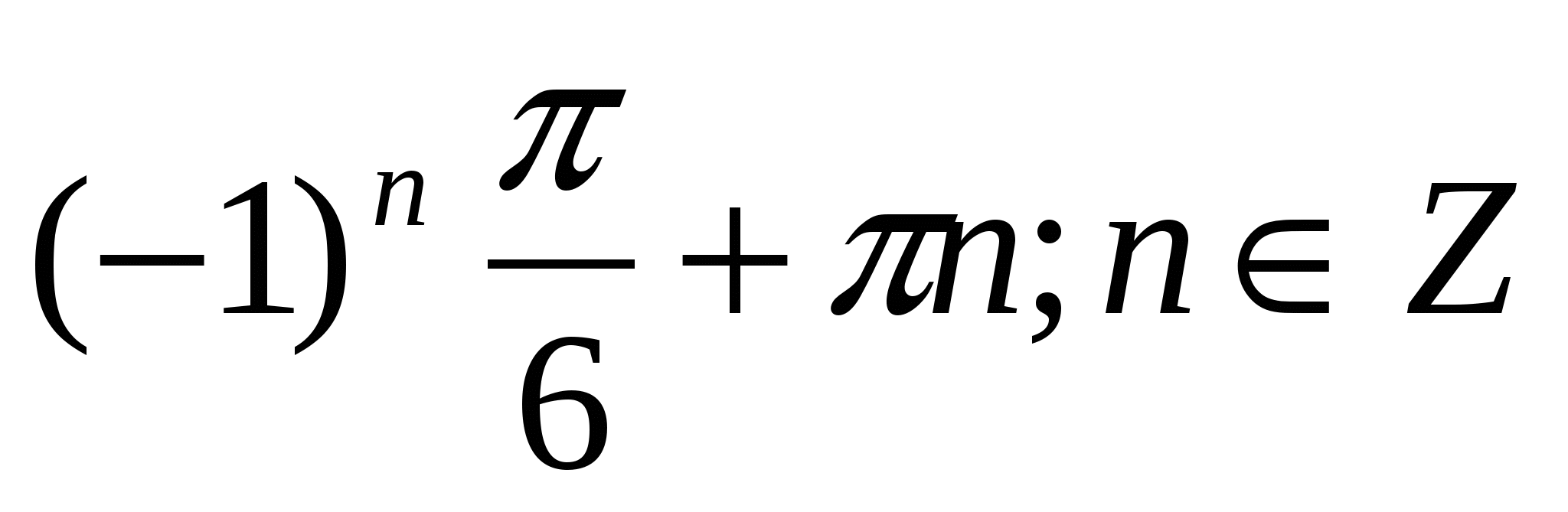
|
|
19)При каких значениях 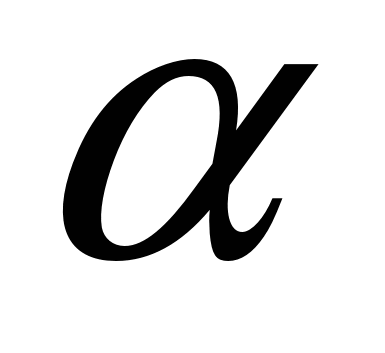 числа числа 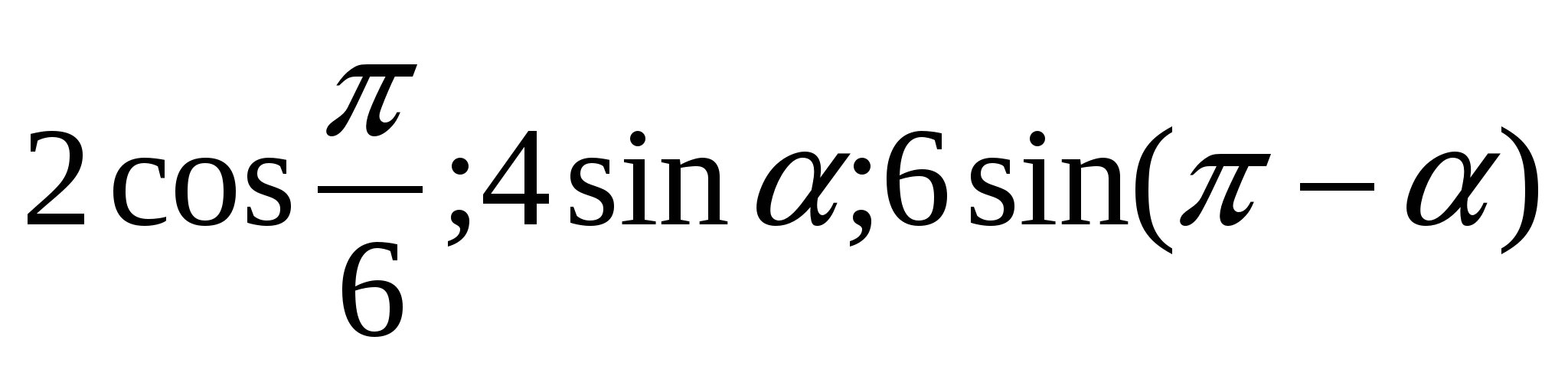 являются последовательными членами арифметической прогрессии. являются последовательными членами арифметической прогрессии.
|
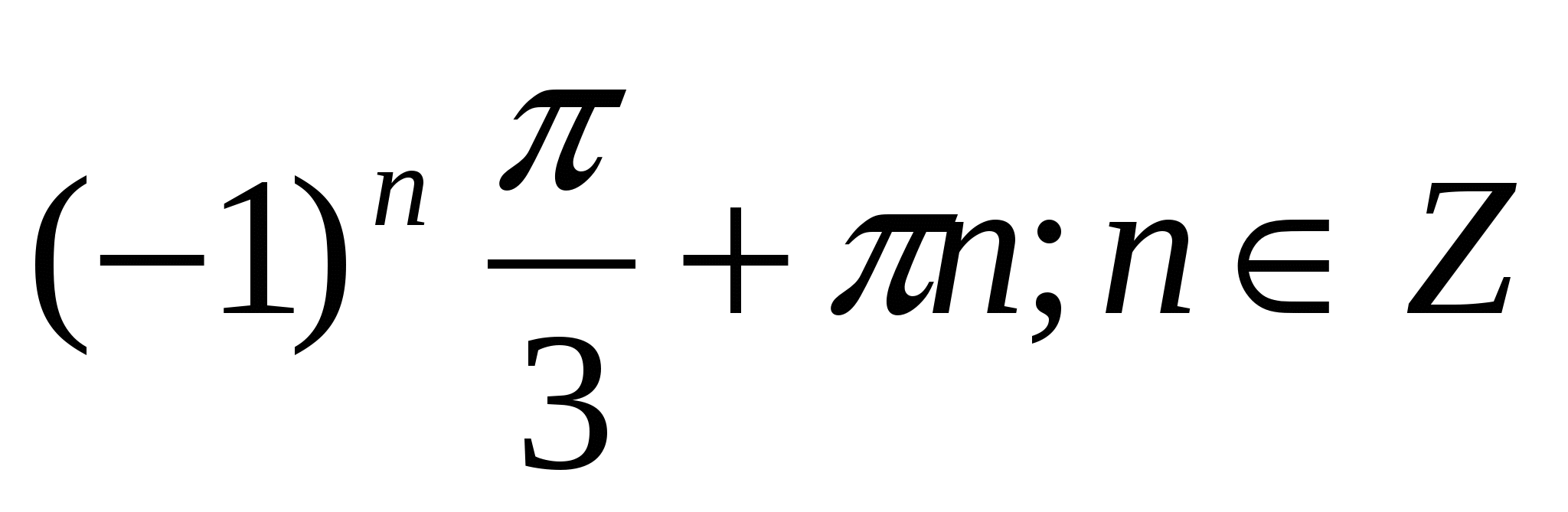 ) )
|
|
20)Даны три последовательные члены арифметической прогрессии sin x, sin 2x, sin 3x. Найти х.
|
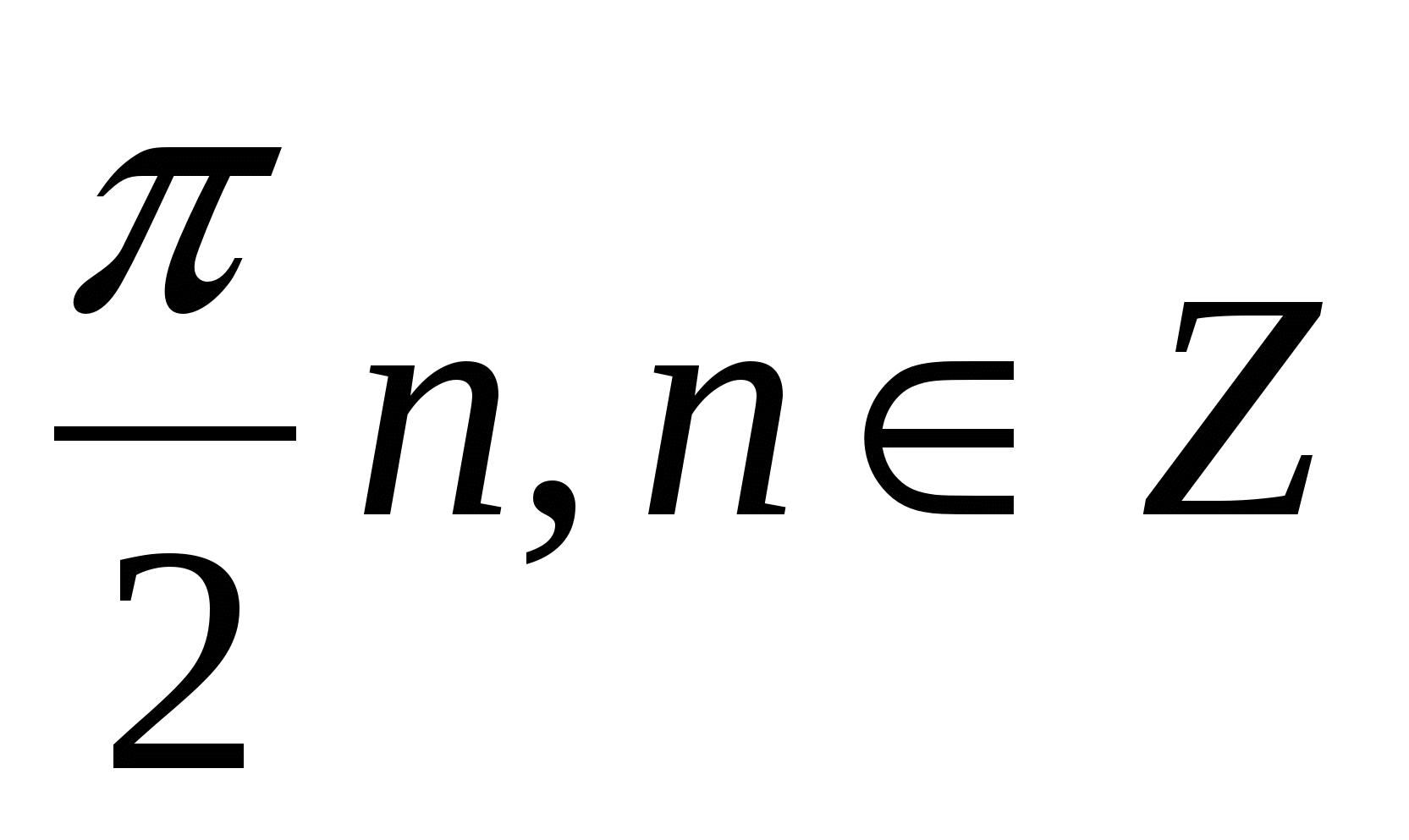
|
С
|
21)Корни уравнения х4-10х2+а = 0 составляют арифметическую прогрессию. Найти а.
|
9
|
|
22)Найти все значения параметра а, при которых уравнение х8+ах4+1 = 0 имеет ровно 4 действительных корня, образующих арифметическую прогрессию.
|
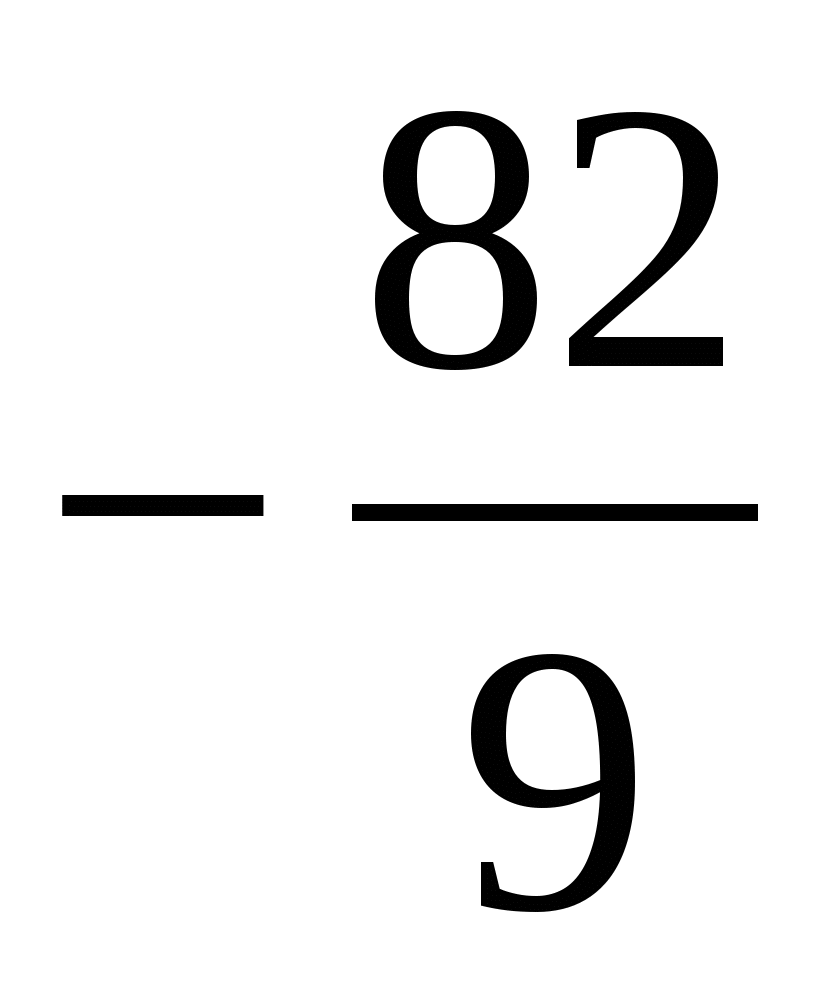
|
 Скачать 35.85 Kb.
Скачать 35.85 Kb.